Representing integer number refers to how the computer stores or represents a number in binary. The computer represents numbers in binary (1's and 0's). However, the computer has a limited amount of space that can be used for each number or variable. This directly impacts the size, or range, of the number that can be represented. For example, a byte (8-bits) can be used to represent 2^8 or 256 different numbers. Those 256 different numbers can be unsigned (all positive) in which case we can represent any number between 0 and 255 (inclusive). If we choose signed (positive and negative values), then we can represent any number between -128 and +127 (inclusive).
If that range is not large enough to handle the intended values, a larger size must be used. For example, a word (16-bits) can be used to represent 2^16 or 65,536 different values, and a double-word (32-bits) can be used to represent 2^32 or 4,294,967,296 different numbers.
The following table shows the ranges associated with typical sizes:
| Size | Size | Unsigned Range | Signed Range |
| Bytes (8-bits) | 2^8 | 0 to 255 | |
| Words (16-bits) | 2^16 | 0 to | |
| Double-words (32-bits) | 2^32 | ||
| Quadword | 2^64 | ||
| Double quadword | 2^128 |
In order to determine if a value can be represented, you will need to know the size of the storage element (byte, word, double-word, quadword, etc.) being used and if the values are signed or unsigned.
- For representing unsigned values within the range of a given storage size, standard binary is used.
- For representing signed values within the range, two's complement is used. Specifically, the two's complement encoding process applies to the values in the negative range. For values within the positive range, standard binary is used.
Two's Complement
The following describes how to find the two's complement representation for negative values (not positive values).
To take the two's complement of a number:
- Take the one's complement (negative)
- Add 1 (in binary)
The same process is used to encode a decimal value into two's complement and from two's complement back to decimal.
Byte Example
To find the byte size (8-bits), two's complement representation of -9 and -12.
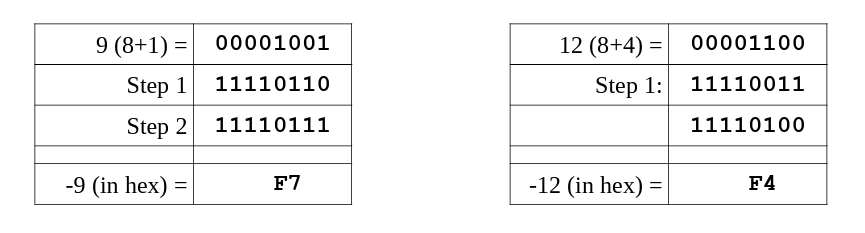
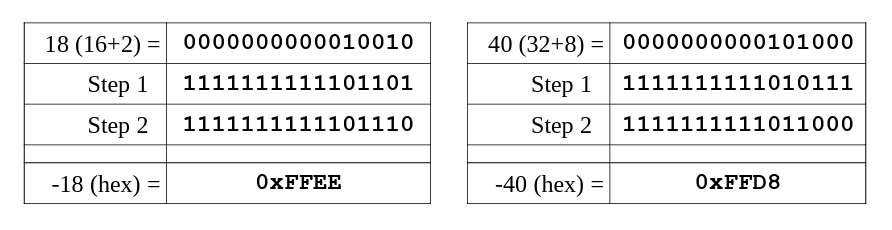
Word Example
To find the word size (16-bits), two's complement representation of -18 and -40.
Unsigned and Signed Addition
As previously noted, the unsigned and signed representation may provide different interpretations for the final value being represented. However, the addition and subtraction operation are the same. For example:
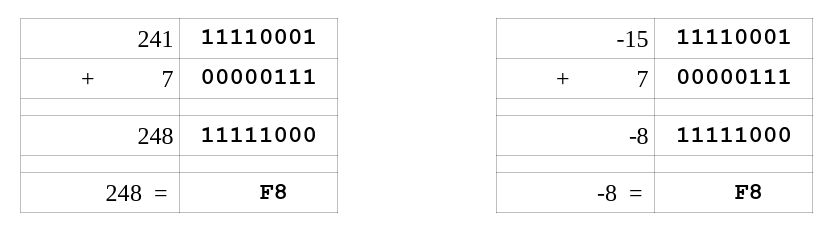
The final result of 0xF8 may be interpreted as 248 for unsigned representation and -8 for a singed representation.