When it comes to searching and sorting data, the binary search tree stands as one of the fundamental data structures. However, its performance hinges greatly on its shape. In the worst-case scenario, it may degrade into a linear structure with a time complexity of O(n). This is where Red-Black Trees shine. They represent a type of balanced binary search tree that adheres to a set of rules ensuring consistent balance. This equilibrium guarantees that operations like insertion, deletion, and searching always maintain a time complexity of O(log n), irrespective of the initial tree shape.

Red-Black Trees possess a remarkable self-balancing capability, ensuring that the tree automatically adjusts its structure following each insertion or deletion operation. This mechanism relies on a straightforward yet potent principle: assigning a color—either red or black—to each node within the tree.

Binary Search Trees and their shortcomings ( The complexity depends on tree height and in the worst case the height can be N , making most of the operations O(N) )

So, we need to somehow make it balanced such that on average the height is logN . Red Black Tree with it magic rotations and colorings seems to somehow do this . But this is not the only data structure to do this .

Understanding Red-Black Trees (Self-Balancing BST)

The Red-Black tree stands out as a binary search tree where every node is distinctly colored red or black. Renowned for its self-balancing nature, it ensures optimal performance even in worst-case scenarios, boasting an efficient running time complexity.

The Red-Black Tree is a self-balancing binary search tree, named after the color properties assigned to its nodes. Developed by Rudolf Bayer in 1972 and further refined by Leonidas J. Guibas and Robert Sedgewick in 1978, Red-Black Trees maintain balance by enforcing five key properties:

Why is this red? Why not any other colors?

It was because the guys who invented this, only had red and black pens to draw, and they choose to color the nodes red.

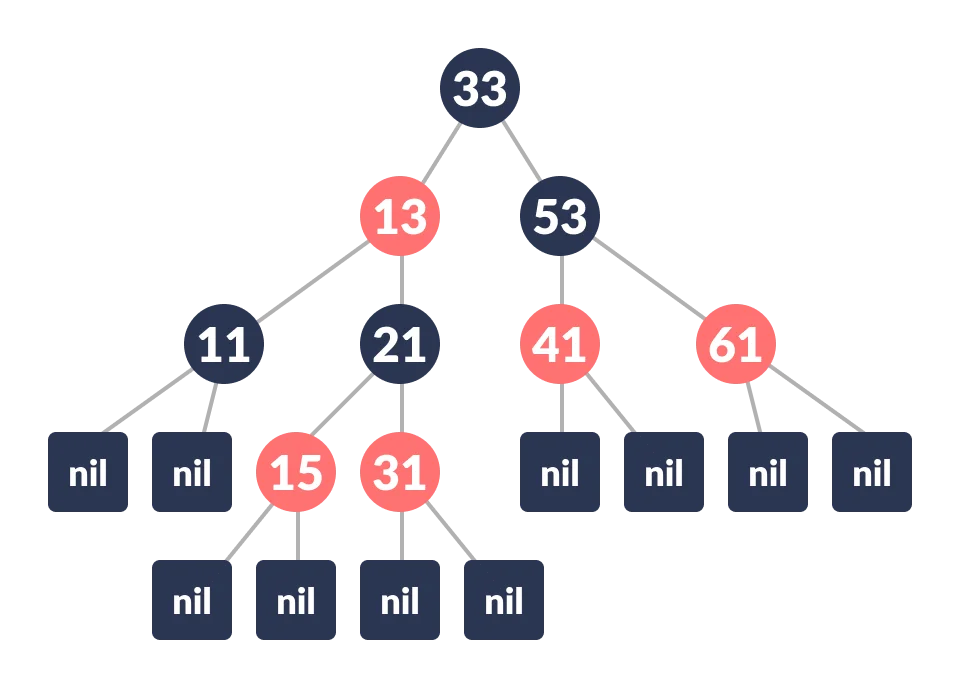
Properties of Red-Black Trees

1 Property 1: Node Coloring

Each node in the Red-Black Tree is either red or black.

         7 (Black)
        / \
   (Red)3   18 (Red)
             / \
        (Black)10  22 (Black)
           / \
      (Red)8   11 (Red)

In this example, every node is colored either red or black.

2 Property 2: Root property

The root node of the tree is always black.

         7 (Black)
        / \
   (Red)3   18 (Red)
             / \
        (Black)10  22 (Black)
           / \
      (Red)8   11 (Red)

The root node (7) is black, satisfying the root property.

3 Property 3: Red Property

No two adjacent nodes (parent and child) can both be red.

         7 (Black)
        / \
   (Red)3   18 (Red)
             / \
        (Black)10  22 (Black)
           / \
      (Red)8   11 (Red)

There are no two adjacent red nodes in the tree, satisfying the red property.

4 Property 4: Black Depth Property

All paths from any node to its descendant null nodes (leaves) contain the same number of black nodes.

Every path from root to a null node must have exactly the same number of black nodes.

null nodes are also sometimes called null leafs.  these are not really nodes.. they are the "nodes" that null pointers point to... so we when we think about counting black nodes we think about how many black nodes there are to every nullptr in the tree

Every leaf (NIL pointer) is black.

         7 (Black)
        / \
   (Red)3   18 (Red)
             / \
        (Black)10  22 (Black)
           / \
      (Red)8   11 (Red)

To check the Black Depth Property, we'll examine paths from the root node (7) to its descendant null nodes (leaves):

• Leaf Node 3: Contains 1 black node on the path (7).
• Leaf Node 8: Contains 2 black nodes on the path (7, 10).
• Leaf Node 11: Contains 2 black nodes on the path (7, 10).
• Leaf Node 22: Contains 2 black nodes on the path (7, 22).

The path to Node 3 contains 1 black node (7), while other paths contain 2 black nodes (from the root node 7 to nodes 10, 8, 11, and 22). This discrepancy violates the Black Depth Property, indicating that this tree does not adhere to the definition of a Red-Black Tree.

5 Property 5: Red-Black Tree Property

Every simple path from a node to its descendant null nodes contains the same number of black nodes.

         7 (Black)
        / \
   (Red)3   18 (Red)
             / \
        (Black)10  22 (Black)
           / \
      (Red)8   11 (Red)

Every simple path from any node to its descendant null nodes contains the same number of black nodes. For example, the path from node 18 to its descendant null nodes (10, 8, and 11) contains 1 black node.

Node

Each node has the following attributes:

• color
• key
• leftChild
• rightChild
• parent (except root node)

Insertion

Insert the new node according to regular binary search tree insertion rules.  Of the 4 colouring rules, the one rule we don't want to break is rule number 4.  Everything we do is to avoid breaking rule 4 (every path from root to every null leaf has same number of black nodes).  Thus, New nodes are added as red nodes.  We then "fix" the tree if any of the rules are broken.

Note that because we inserted a red node to a proper red-black tree, the only 2 rules that might be broken are:

rule 2: root must be black

rule 3: red node must have black children

Rule 1 is pretty much not broken as we coloured it red.  We also won't break rule 4 because we added a red node so the number of black nodes has not increased.

General Insertion Algorithm

To insert into a red-black tree:

1. Find the correct empty tree (like bst) and insert new node as a red node.
2. Working way up to the tree back to parent fix the tree so that the red-black tree rules are maintained.

Fixing Nodes:

• If root becomes red, change it to black.
  • This won't break any rules because you are just adding 1 black node to every branch of the tree, the number of black nodes increase by 1 everywhere. This can only happen as the root as it is the only node that is part of every path from root to null leaf.
• If there are two red nodes in a row:
  • Identify the following nodes:
    • Upper red node as the Parent (P)
    • The lower red node as the Child (C)
    • Parent of parent as Grandparent (G)
    • Sibling of Parent as Parent' sibling (PS)
• If the PS is black
  • Perform a rotation (look at G->P->C, if they form a straight line do a zig-zag (single) rotation, if there is a bend, do a zig-zag (double rotation))
  • After rotation exchange G's color with the node that took over G's spot. In other words:
    • Make which ever node (depends if it was zigzig or zigzag rotation… it will either be P or C) that took over G's node black
    • Make G red.
• if the PS is red
  • exchange the color of the grand parent with its two children. In other words
    • G becomes red
    • P and PS becomes black

Example:

Starting with an empty tree let us take a look at how red-black tree insertions work.

In the pictures below, null nodes (empty subtrees) are denoted as black circles:

Insert 30

All nodes are inserted as red nodes:

If the root is red, make it black:

Insert 50

Insert 50 as a red node, parent is black so we don't have to change anything.

Insert 40

Inserting 40 as a red node.

Two red nodes in a row. Identify G, P, PS and C

• P - parent (upper red) - 50
• C - child (lower red) - 40
• G - grandparent - 30
• PS - parent's sibling - null node to left of 30

What we do depends on colors of PS. In this case PS is black, so we will be fixing this with a rotation.

The type of rotation depends on the configuration of G, P and C. If the path is from G to C is straight (both left or both right) do a zigzig (single) rotation. If it is angled (left then right or right then left) we need to do a zigzag (double) rotation.

In this case, we need to do a zig zag (double) rotation.

Rotate first 40 and 50

then rotate again with 30 and 40, this time doing a color swap. A zigzag rotation is just an step that is needed to make the insertion path go in the same direction.

After rotations are complete, we exchange the color between the node that took over G's spot (40 in this case) and G.  Thus,  40 becomes black and 30 becomes red.

Insert 20

Inserting 20 as a red node.

Two red nodes in a row. Identify G, P, PS and C

• P  - parent (upper red) - 30
• C  - child (lower red) - 20
• G - grandparent - 40
• PS - parent's sibling - null node to left of 50

What we do depends on color of PS. In this case PS is red. Thus we exchange colors between G and its two children:

Doing so breaks rule 2: roots must be black.  Thus, we need to fix that. As it is the root, we can just change it to black without causing other problems.

Insert 10

Inserting 10 as a red node.

Two red nodes in a row. Identify G, P, PS and C

• P  - parent (upper red) -20
• C  - child (lower red) - 10
• G - grandparent 30
• PS - parent's sibling - null node to right of 30

What we do depends on color of PS.  In this case, the parent's sibling is black (null nodes are black).  Thus, we will fix this with a rotation.  Rotations are always done with G as the root of the rotation (the A in the rotation diagram)

This time, the path from G to P to C is "left" then "left". Thus, we only need to perform a single rotation, followed by swapping the colors of G and the node that took G's spot.

Finally we get:

Rotations

There are two main types of rotations in RB trees: left rotations and right rotations.

1 Left Rotation:

A left rotation involves reconfiguring the structure of the tree to rotate a node and its right subtree to the left. This operation is typically performed when a node is leaning towards the right side and needs to be balanced.

      A                   B
     / \                 / \
    a   B      ===>     A   c
       / \             / \
      b   c           a   b