What is a Trie(Prefix Tree) Data Structure?
A Trie is a tree-like data structure used to store a collection of strings. It is commonly used for fast searching of strings, particularly when there is a large and dynamic set of strings. The name "Trie" comes from the word "reTRIEval".
It is commonly used for efficient retrieval and storage of keys in a large dataset. The structure supports operations such as insertion, search, and deletion of keys, making it a valuable tool in fields like computer science and information retrieval.
Trie data structure is faster than binary search trees and hash tables for storing and retrieving data. Trie data structure is also known as a Prefix Tree or a Digital Tree. We can do prefix-based searching easily with the help of a Trie.
- It is tree-based data structure used for storing collection of strings.
- The word trie comes from the word reTRIEval which means to find or get something back.
- Each node in the Trie represents a single character of the string.
- The root node represents an empty string, and each subsequent level represents one more character in the string.
- Each node can have multiple children.
- A dictionary can be implemented efficiently using the trie.
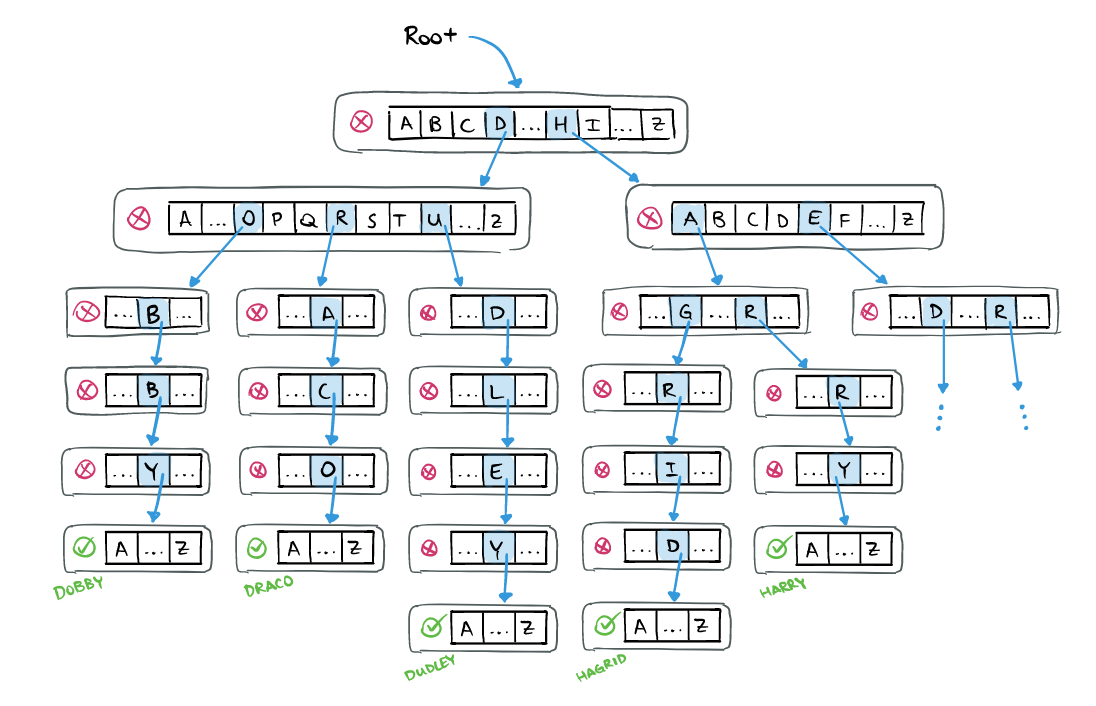
Below is the pictorial representation of the trie, we have 5 words, and then we inserted these words in our trie.

- The green highlighted nodes, represents the
endOfWordBoolean value of a word which in turn means that this particular word is completed at this node. - The root node of a trie is empty so that it can refer to all the members of the alphabet the trie is using to store, and the children nodes of any node of a trie can have at most 26 children.
- Tries are not balanced in nature, unlike AVL trees.
Why Use a Trie Data Structure?
Up to this point if we ask ourselves what would be the fastest ways to retrieve values from a data structure, then no doubtly a single name comes to our mind, which is hash table.
A Trie data structure is used for efficient storage and retrieval of data. Another data structure which does the same operation is a Hash Table. However, a trie data structure can be more efficient to handle these operations than the Hash Table. A trie data structure supports prefix-based searching, which is not efficiently possible with a Hash Table. Prefix-based searching allows us to efficiently find all strings in a collection that begin with a given prefix. This feature is extremely useful in applications such as autocomplete and spell checkers.
Advantages of Trie over Hash Table:
- Prefix-based Searching:
- Trie data structure supports prefix-based searching efficiently, which is not possible with a Hash Table.
- Prefix-based Searching allows us to efficiently find all strings in a collection that begin with a given prefix.
- No Collisions:
- Trie data structure does not suffer from collisions, unlike a Hash Table.
- This ensures better worst-case time complexity in Trie compared to a poorly implemented Hash Table.
- No Hash Functions:
- Trie data structure does not use hash functions, eliminating the overhead of computing hash values.
- In a Hash Table, the efficiency heavily depends on the quality of the hash function.
- Efficient Searching:
- Searching for a string in a Trie data structure is done in
O(k)time complexity, where k is the number of characters in the query string. - It may take even less than
O(k)time when the query string is not present in the Trie.
- Searching for a string in a Trie data structure is done in
Representation of Trie Node
A Trie data structure consists of nodes connected by edges. Each node represents a character or a part of a string. The root node, the starting point of the Trie, represents an empty string. Each edge emanating from a node signifies a specific character. The path from the root to a node represents the prefix of a string stored in the Trie.
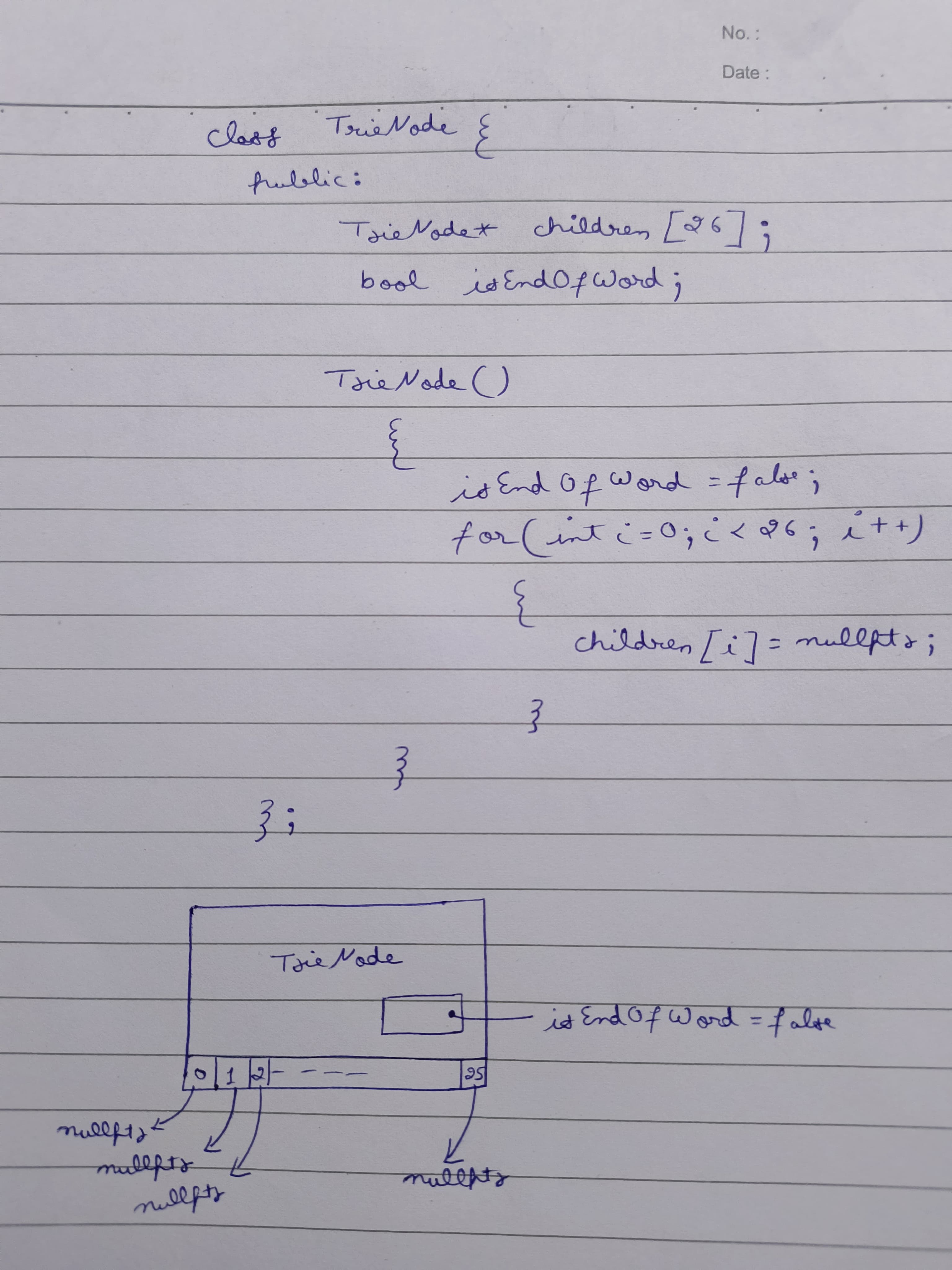
Each node in a Trie contains the following components:
- A pointer to its child nodes.
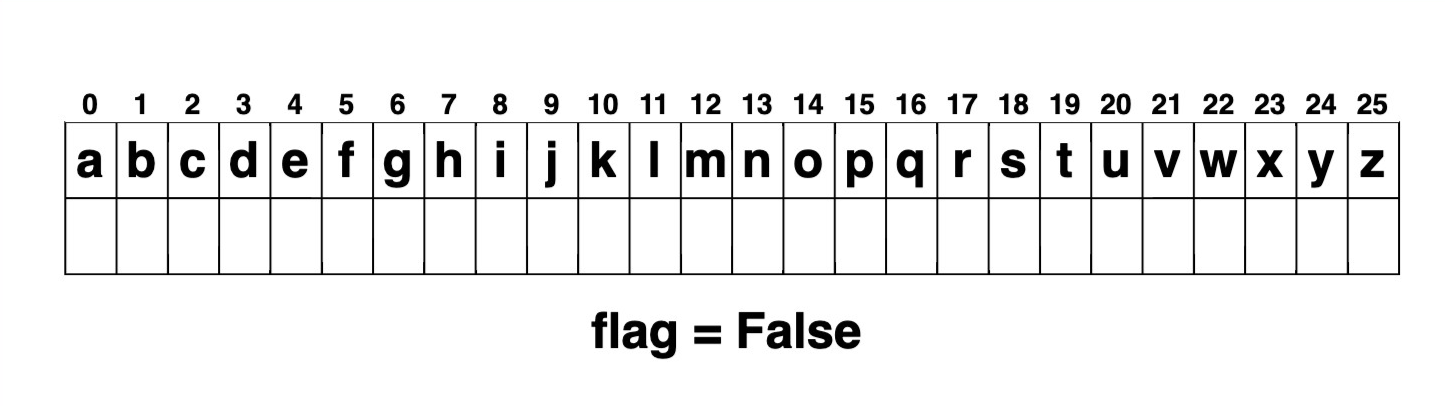
- A flag to indicate whether the node represents the end of a word.
- Additional metadata, if required.
const int ALPHABET_SIZE = 26;
class TrieNode {
public:
TrieNode* children[ALPHABET_SIZE];
bool isEndOfWord;
TrieNode() {
isEndOfWord = false;
for (int i = 0; i < ALPHABET_SIZE; i++) {
children[i] = nullptr;
}
}
};const int ALPHABET_SIZE = 26;: This line declares a constant ALPHABET_SIZE with a value of 26. This constant represents the size of the alphabet being used. In this case, it's set to 26, assuming the standard English alphabet (a-z).class TrieNode { ... };: This defines the TrieNode class. Each node in the Trie structure will be an instance of this class.- Inside the
TrieNodeclass:TrieNode* children[ALPHABET_SIZE];: This line declares an array calledchildrenof sizeALPHABET_SIZE, where each element of the array is a pointer to aTrieNode. This array represents the children nodes of the current node for each character in the alphabet. For example, children[0] represents the child node for character 'a', children[1] for 'b', and so on.bool isEndOfWord;: This boolean variable indicates whether the current node marks the end of a word in the Trie. IfisEndOfWordis true, it means that a word ends at this node in the Trie.TrieNode() { ... }: This is the constructor of theTrieNodeclass. It initializes theisEndOfWordvariable to false, indicating that by default, the node does not mark the end of a word. It also initializes each element of the children array tonullptr, indicating that initially, there are no children nodes.
for (int i = 0; i < ALPHABET_SIZE; i++) { ... }: This loop initializes each element of thechildrenarray tonullptr. It iterates from 0 toALPHABET_SIZE - 1and assignsnullptrto each element of the array.
Trie Operations:
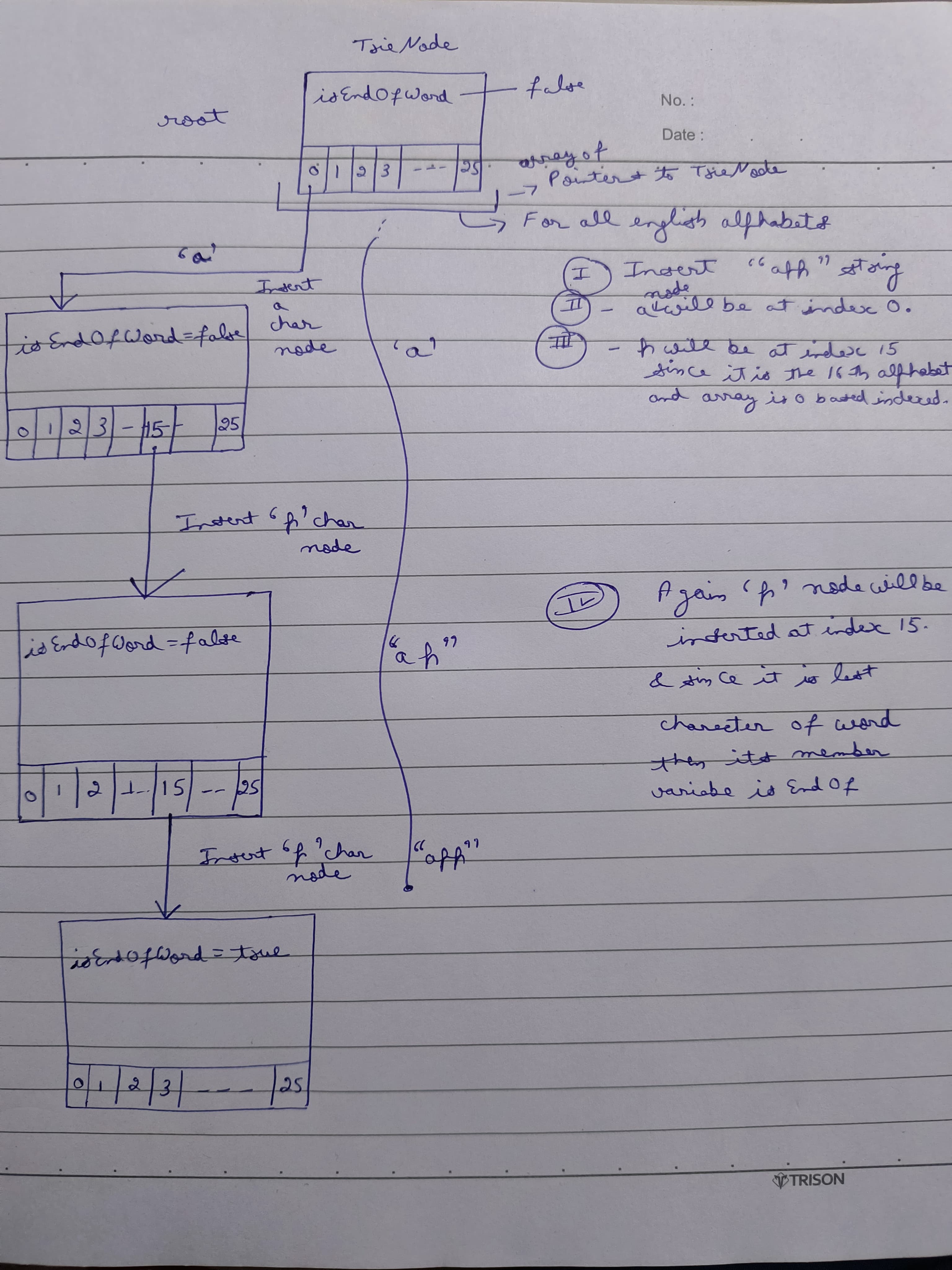
1 Insertion:
The insertion operation in a Trie involves traversing the trie from the root node to the node representing the string to be inserted. If the characters of the string are not present in the trie, new nodes are created. The end of the string is marked by setting a flag in the last node of the string.
Algorithm:
- Start from the root node.
- For each character in the string to be inserted:
- If the character is not present in the trie, create a new node and move to it.
- If the character is present, move to the corresponding node.
- After processing all the characters of the string, mark the last node as the end of the string.
Code Implementation in C++:
#include <iostream>
using namespace std;
const int ALPHABET_SIZE = 26;
// Trie Node class
class TrieNode {
public:
TrieNode* children[ALPHABET_SIZE]; // Array to store child nodes for each character
bool isEndOfWord; // Flag to indicate end of a word
// Constructor
TrieNode() {
isEndOfWord = false;
// Initialize all child nodes to nullptr
for (int i = 0; i < ALPHABET_SIZE; i++) {
children[i] = nullptr;
}
}
};
// Trie class
class Trie {
private:
TrieNode* root; // Root node of the trie
public:
// Constructor
Trie() {
root = new TrieNode();
}
// Function to insert a word into the trie
void insert(string word) {
TrieNode* current = root;
// Traverse through each character of the word
for (char c : word) {
int index = c - 'a'; // Calculate index of the character
// If the child node for the character doesn't exist, create a new node
if (!current->children[index]) {
current->children[index] = new TrieNode();
}
// Move to the child node
current = current->children[index];
}
// Mark the last node as end of word
current->isEndOfWord = true;
}
};
int main() {
// Create a trie object
Trie trie;
// Insert some words into the trie
trie.insert("apple");
trie.insert("app");
trie.insert("banana");
trie.insert("bat");
trie.insert("ball");
return 0;
}
2 Searching:
To search for a string in a Trie, we start from the root node and traverse down the Trie. For each character in the string:
1. Start from the root node.
2. For each character in the search string:
- If a child node corresponding to the character doesn't exist, the search string is not present in the Trie.
- Move to the child node corresponding to the character.
3. If all characters are found and the last node is marked as the end of a word, the search string is present in the Trie.
Code Implementation in C++:
#include <iostream>
using namespace std;
const int ALPHABET_SIZE = 26;
class TrieNode {
public:
TrieNode* children[ALPHABET_SIZE];
bool isEndOfWord;
TrieNode() {
isEndOfWord = false;
// Initialize all children nodes to nullptr
for (int i = 0; i < ALPHABET_SIZE; i++) {
children[i] = nullptr;
}
}
};
class Trie {
TrieNode* root;
public:
Trie() {
// Create root node when Trie is initialized
root = new TrieNode();
}
void insert(string word) {
TrieNode* current = root;
// Traverse through each character of the word
for (int i = 0; i < word.length(); i++) {
int index = word[i] - 'a'; // Calculate index for the character
// If current character's node doesn't exist, create a new node
if (!current->children[index]) {
current->children[index] = new TrieNode();
}
// Move to the next node
current = current->children[index];
}
// Mark the end of the word
current->isEndOfWord = true;
}
bool search(string word) {
TrieNode* current = root;
// Traverse through each character of the word
for (int i = 0; i < word.length(); i++) {
int index = word[i] - 'a'; // Calculate index for the character
// If current character's node doesn't exist, word doesn't exist
if (!current->children[index]) {
return false;
}
// Move to the next node
current = current->children[index];
}
// If end of word flag is set, word exists
return (current != nullptr && current->isEndOfWord);
}
};
int main() {
Trie* trie = new Trie();
// Insert words into Trie
trie->insert("hello");
trie->insert("world");
// Search for words in Trie
cout << "Searching for 'hello': " << (trie->search("hello") ? "Found" : "Not Found") << endl;
cout << "Searching for 'world': " << (trie->search("world") ? "Found" : "Not Found") << endl;
cout << "Searching for 'hi': " << (trie->search("hi") ? "Found" : "Not Found") << endl;
return 0;
}
3 Deletion:
Deletion in a Trie involves removing a key from the Trie. The deletion process is a bit more complex compared to insertion and search due to the following reasons:
- When deleting a node, you must consider whether the node is a part of another key or not.
- If the node to be deleted has children, it shouldn't be removed. Instead, it should be marked as non-leaf.
Algorithm:
The deletion process involves several steps:
- Start from the root and find the node containing the last character of the key to be deleted.
- Delete the key from the bottom up.
- If a node becomes non-leaf (i.e., it doesn't have any child nodes) and is not the end of another key, it can be removed.
Code Implementation in C++:
#include <iostream>
using namespace std;
const int ALPHABET_SIZE = 26;
// Trie Node class
class TrieNode {
public:
TrieNode* children[ALPHABET_SIZE];
bool isEndOfWord;
TrieNode() {
isEndOfWord = false;
// Initialize all children nodes to nullptr
for (int i = 0; i < ALPHABET_SIZE; i++) {
children[i] = nullptr;
}
}
};
// Trie class
class Trie {
public:
TrieNode* root;
Trie() {
root = new TrieNode();
}
// Function to insert a key into the Trie
void insert(string key) {
TrieNode* current = root;
for (int i = 0; i < key.length(); i++) {
int index = key[i] - 'a';
// Create a new node if the character is not present
if (!current->children[index])
current->children[index] = new TrieNode();
current = current->children[index];
}
// Mark the last node as the end of the key
current->isEndOfWord = true;
}
// Function to check if a node is empty (has no children)
bool isEmpty(TrieNode* node) {
for (int i = 0; i < ALPHABET_SIZE; i++) {
if (node->children[i])
return false;
}
return true;
}
// Recursive helper function for deleting a key from the Trie
TrieNode* deleteHelper(TrieNode* node, string key, int depth = 0) {
// If the node doesn't exist, return nullptr
if (!node)
return nullptr;
// If we have reached the end of the key
if (depth == key.length()) {
// If the node is a part of another key, just mark it as non-end node
if (node->isEndOfWord)
node->isEndOfWord = false;
// If the node is empty and not an end node of another key, delete it
if (isEmpty(node)) {
delete (node);
node = nullptr;
}
return node;
}
// Find the index corresponding to the current character in the key
int index = key[depth] - 'a';
// Recursively call deleteHelper for the next character in the key
node->children[index] = deleteHelper(node->children[index], key, depth + 1);
// If the node becomes empty and not an end node of another key, delete it
if (isEmpty(node) && node->isEndOfWord == false) {
delete (node);
node = nullptr;
}
return node;
}
// Function to remove a key from the Trie
void remove(string key) {
if (key.empty())
return;
root = deleteHelper(root, key);
}
};
int main() {
Trie trie;
// Insert some keys into the Trie
trie.insert("apple");
trie.insert("app");
trie.insert("orange");
trie.insert("ornament");
cout << "Trie before deletion:" << endl;
// Display Trie before deletion
// Delete a key from the Trie
trie.remove("ornament");
cout << "Trie after deletion:" << endl;
// Display Trie after deletion
return 0;
}4 Prefix Searching
In a Trie, each node represents a single character of a word. By traversing the Trie from the root node based on the characters of the prefix, you can find all the words that have the given prefix.
Algorithm:
The algorithm for prefix searching involves the following steps:
- Start from the root node.
- Traverse the Trie based on the characters of the prefix.
- Once you reach the end of the prefix, recursively find all the words under that node.
Code Implementation in C++:
#include <iostream>
#include <vector>
using namespace std;
const int ALPHABET_SIZE = 26;
class TrieNode {
public:
TrieNode* children[ALPHABET_SIZE];
bool isEndOfWord;
TrieNode() {
isEndOfWord = false;
for (int i = 0; i < ALPHABET_SIZE; i++) {
children[i] = nullptr;
}
}
};
class Trie {
public:
TrieNode* root;
Trie() {
root = new TrieNode();
}
// Function to insert a key into the Trie
void insert(string key) {
TrieNode* current = root;
for (int i = 0; i < key.length(); i++) {
int index = key[i] - 'a';
if (!current->children[index])
current->children[index] = new TrieNode();
current = current->children[index];
}
current->isEndOfWord = true;
}
// Function to search for a key in the Trie
bool search(string key) {
TrieNode* current = root;
for (int i = 0; i < key.length(); i++) {
int index = key[i] - 'a';
if (!current->children[index])
return false;
current = current->children[index];
}
return (current != nullptr && current->isEndOfWord);
}
// Function to find all words with a given prefix
vector<string> findWordsWithPrefix(string prefix) {
vector<string> result;
TrieNode* current = root;
// Traverse to the end of the prefix
for (int i = 0; i < prefix.length(); i++) {
int index = prefix[i] - 'a';
if (!current->children[index])
return result; // Prefix not found
current = current->children[index];
}
// Call recursive function to find all words with the given prefix
findWordsWithPrefixHelper(current, prefix, result);
return result;
}
private:
// Recursive helper function to find all words with the given prefix
void findWordsWithPrefixHelper(TrieNode* node, string prefix, vector<string>& result) {
if (node == nullptr)
return;
// If the current node marks the end of a word, add it to the result
if (node->isEndOfWord)
result.push_back(prefix);
// Traverse all child nodes
for (int i = 0; i < ALPHABET_SIZE; i++) {
if (node->children[i]) {
// Append the current character to the prefix and recursively call the function
findWordsWithPrefixHelper(node->children[i], prefix + char('a' + i), result);
}
}
}
};
int main() {
Trie trie;
// Insert some keys into the Trie
trie.insert("apple");
trie.insert("app");
trie.insert("orange");
trie.insert("ornament");
string prefix = "or";
vector<string> wordsWithPrefix = trie.findWordsWithPrefix(prefix);
if (wordsWithPrefix.size() == 0)
cout << "No words found with the prefix '" << prefix << "'" << endl;
else {
cout << "Words with the prefix '" << prefix << "': ";
for (auto word : wordsWithPrefix)
cout << word << " ";
cout << endl;
}
return 0;
}5 Print All Words:
Algorithm:
- Start with the root of the Trie.
- Recursively traverse each branch of the Trie.
- At each node, if it marks the end of a word, add the current prefix to the list of words.
- Recursively call the function for each child node of the current node.
Code Implementation in C++:
#include <iostream>
#include <vector>
using namespace std;
const int ALPHABET_SIZE = 26;
class TrieNode {
public:
TrieNode* children[ALPHABET_SIZE];
bool isEndOfWord;
TrieNode() {
isEndOfWord = false;
for (int i = 0; i < ALPHABET_SIZE; i++) {
children[i] = nullptr;
}
}
};
class Trie {
public:
TrieNode* root;
Trie() {
root = new TrieNode();
}
// Function to insert a key into the Trie
void insert(string key) {
TrieNode* current = root;
for (int i = 0; i < key.length(); i++) {
int index = key[i] - 'a';
if (!current->children[index])
current->children[index] = new TrieNode();
current = current->children[index];
}
current->isEndOfWord = true;
}
// Function to search for a key in the Trie
bool search(string key) {
TrieNode* current = root;
for (int i = 0; i < key.length(); i++) {
int index = key[i] - 'a';
if (!current->children[index])
return false;
current = current->children[index];
}
return (current != nullptr && current->isEndOfWord);
}
// Function to find all words with a given prefix
vector<string> findWordsWithPrefix(string prefix) {
vector<string> result;
TrieNode* current = root;
// Traverse to the end of the prefix
for (int i = 0; i < prefix.length(); i++) {
int index = prefix[i] - 'a';
if (!current->children[index])
return result; // Prefix not found
current = current->children[index];
}
// Call recursive function to find all words with the given prefix
findWordsWithPrefixHelper(current, prefix, result);
return result;
}
// Function to print all words in the Trie
void printAllWords() {
vector<string> words;
string prefix = "";
printAllWordsHelper(root, prefix, words);
cout << "All words in the Trie: ";
for (auto word : words)
cout << word << " ";
cout << endl;
}
private:
// Recursive helper function to find all words with the given prefix
void findWordsWithPrefixHelper(TrieNode* node, string prefix, vector<string>& result) {
if (node == nullptr)
return;
// If the current node marks the end of a word, add it to the result
if (node->isEndOfWord)
result.push_back(prefix);
// Traverse all child nodes
for (int i = 0; i < ALPHABET_SIZE; i++) {
if (node->children[i]) {
// Append the current character to the prefix and recursively call the function
findWordsWithPrefixHelper(node->children[i], prefix + char('a' + i), result);
}
}
}
// Recursive helper function to print all words in the Trie
void printAllWordsHelper(TrieNode* node, string prefix, vector<string>& words) {
if (node == nullptr)
return;
// If the current node marks the end of a word, add it to the words vector
if (node->isEndOfWord)
words.push_back(prefix);
// Traverse all child nodes
for (int i = 0; i < ALPHABET_SIZE; i++) {
if (node->children[i]) {
// Append the current character to the prefix and recursively call the function
printAllWordsHelper(node->children[i], prefix + char('a' + i), words);
}
}
}
};
int main() {
Trie trie;
// Insert some keys into the Trie
trie.insert("apple");
trie.insert("app");
trie.insert("orange");
trie.insert("ornament");
// Print all words in the Trie
trie.printAllWords();
return 0;
}
Leave a comment
Your email address will not be published. Required fields are marked *
