Overview
The Merge Interval Pattern is a common approach to solve problems related to intervals. It involves sorting intervals based on their start time, merging overlapping intervals, and producing a set of non-overlapping intervals.
Understanding
This pattern describes an efficient technique to deal with overlapping intervals. In a lot of problems involving intervals, we either need to find overlapping intervals or merge intervals if they overlap.
Given two intervals (a and b), there will be six different ways the two intervals can relate to each other:
aandbdo not overlapaandboverlap,bends afteraacompletely overlapsbaandboverlap,aends afterbbcompletely overlapsaaandbdo not overlap
Understanding the above six cases will help us in solving all interval related problems.

If a.start ≤ b.start, only 1, 2 and 3 are possible from the above scenarios.
Our goal is to merge the interval whenever they overlap. For the two overlapping scenarios 2 and 3, this is how we will merge them:
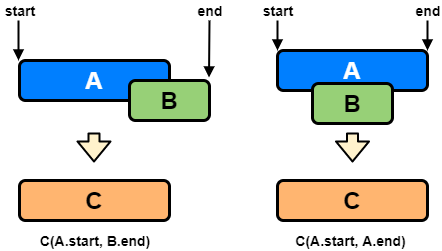
The diagram above clearly show a merging approach. Our algorithm will look like this:
1 Sort the interval on the start time to ensure a.start ≤ b.start.
2 If a overlaps b (i.e., b.start ≤ b.start), we need to merge them into a new interval c.
We are going to merge them into a new interval c such that:
c.start = a.start
c.end = max(a.end, b.end)3 We will keep repeating the above two steps to merge c with the next interval if it overlaps with c.
Steps Involved in solving it
The steps involved in the Merge Interval Pattern are:
- Sort: Sort the intervals based on their start time.
- Merge: Merge the intervals that overlap.
- Output: Output the non-overlapping intervals.
Example 1:
Intervals: [[1,4], [2,5], [7,9]]
Output: [[1,5], [7,9]]
Explanation: Since the first two intervals [1,4] and [2,5] overlap, we
merged them into one [1,5].Example 2:
Intervals: [[6,7], [2,4], [5,9]]
Output: [[2,4], [5,9]]
Explanation: Since the intervals [6,7] and [5,9] overlap, we merged
them into one [5,9].Code
Let's illustrate the Merge Interval Pattern with an example:
#include <iostream>
#include <vector>
#include <algorithm>
struct Interval {
int start;
int end;
Interval(int s, int e) : start(s), end(e) {}
};
std::vector<Interval> mergeIntervals(std::vector<Interval>& intervals) {
if(intervals.empty()) return {};
std::sort(intervals.begin(), intervals.end(), [](const Interval& a, const Interval& b){
return a.start < b.start;
});
std::vector<Interval> merged;
merged.push_back(intervals[0]);
for(int i = 1; i < intervals.size(); ++i) {
if(intervals[i].start <= merged.back().end) {
merged.back().end = std::max(merged.back().end, intervals[i].end);
} else {
merged.push_back(intervals[i]);
}
}
return merged;
}
int main() {
std::vector<Interval> intervals = {{1,3}, {2,6}, {8,10}, {15,18}};
std::vector<Interval> mergedIntervals = mergeIntervals(intervals);
std::cout << "Merged Intervals: ";
for(auto interval : mergedIntervals) {
std::cout << "[" << interval.start << ", " << interval.end << "] ";
}
std::cout << std::endl;
return 0;
}
Leave a comment
Your email address will not be published. Required fields are marked *

