Problem Statement

Given an integer n, generate all combinations of well-formed parentheses that consist of exactly n pairs of opening and closing parentheses. The formed length would be 2*n.

LeetCode

https://leetcode.com/problems/generate-parentheses/description/

Constraints

1 <= n <= 8

• The constraint 1 <= n <= 8 typically indicates that:
  • n is small — it's a number between 1 and 8.
  • You can use algorithms with high time complexity, such as brute-force, backtracking, or recursion with permutations, because the total number of possibilities will be small.

Examples

Example 1:

Input: n = 3
Output:[
        "((()))",
        "(()())",
        "(())()",
        "()(())",
        "()()()"
       ]

Example 2:

Input: n = 2
Output: [
         "(())",
         "()()"
        ]

Example 3:

Input: n = 1
Output: [
         "()"
        ]

Constraints for Well-Formed Parentheses:

To be considered a well-formed (valid) parentheses combination:

1. The number of opening parentheses '(' should always be equal to the number of closing parentheses ')'.
2. At any point in the combination, the number of closing parentheses ')' should not exceed the number of opening parentheses '('. If it does, the combination is invalid.

Different Approaches

1️⃣ Recursion

The idea is to build the parentheses string recursively, ensuring that at any point:

1. We can add an opening parenthesis ( if we haven’t used all n opening parentheses yet.
2. We can add a closing parenthesis ) only if the number of closing parentheses is less than the number of opening parentheses used so far.

The recursive approach is a classic depth-first search (DFS) where we try to build valid parentheses strings by adding an open ( or a close ) at each step, ensuring that:

1. We can only add an open ( if we have fewer than n open parentheses.
2. We can only add a close ) if the number of close parentheses is less than the number of open parentheses.

Recursive Algorithm:

1. Start with an empty string and n as the input for the number of pairs of parentheses.
2. At each step, you have two options:
   • Add an open ( parenthesis if you haven’t used all n open parentheses.
   • Add a close ) parenthesis if the number of close parentheses is less than the number of open parentheses.
3. When the string reaches a length of 2 * n (which means all open and close parentheses have been used), add it to the result.

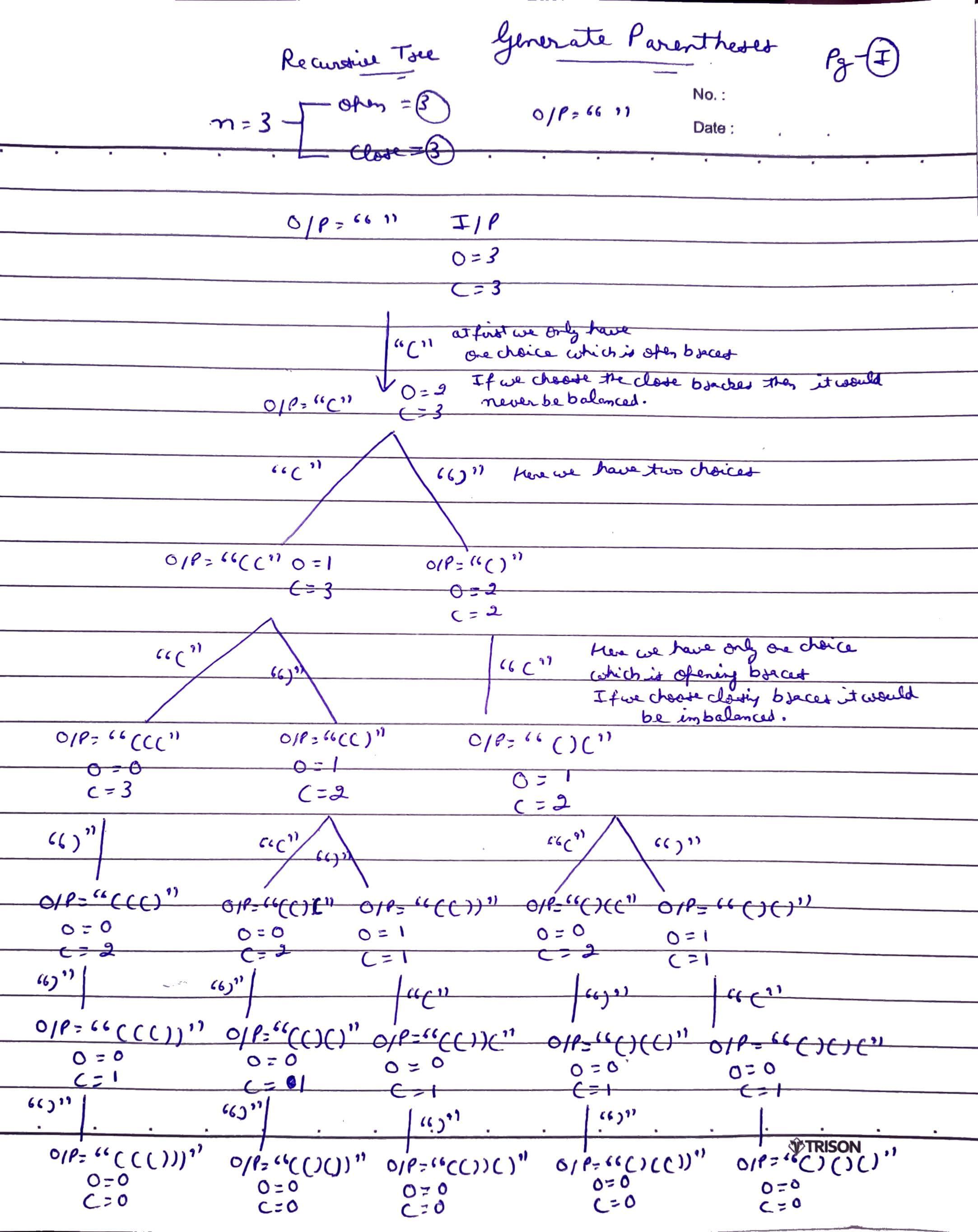
Recursion Tree:

Code:

#include <iostream>
#include <vector>
#include <string>
using namespace std;

void generateParenthesisRec(int open, int close, string current, vector<string>& result) {
    // Base case: If the current string is valid and complete
    if (open == 0 && close == 0) {
        result.push_back(current);
        return;
    }
    
    // Recursive case: Try to add open and close parentheses
    if (open > 0) {
        generateParenthesisRec(open - 1, close, current + "(", result);
    }
    if (close > open) {
        generateParenthesisRec(open, close - 1, current + ")", result);
    }
}

vector<string> generateParenthesis(int n) {
    vector<string> result;
    generateParenthesisRec(n, n, "", result);
    return result;
}

int main() {
    int n = 3;
    vector<string> result = generateParenthesis(n);
    
    for (const string &s : result) {
        cout << s << endl;
    }
    return 0;
}

Visualization of the Recursive Process for n = 3:

We start with n = 3 pairs of parentheses. At each step, we can either add an open parenthesis ( if open > 0 or a close parenthesis ) if close > open.

Here’s a recursive tree that illustrates the process:

                      ""
                    /         \
                  "("          ""
                /    \           \
            "(("       "()"      ""
           /   \       /   \             \
       "((("   "(()"  "()("  "()"          ""
      /    \   /   \    /   \    \           \
 "((())" "(()()" "()()"  "()" "()("         ""
    |       |       |     |     |              |
"((()))" "(()())" "(())()" "()(())" "()()()"

Detailed Walkthrough:

At each node in the recursion tree:

• Open parentheses (() are added if there are still open parentheses left.
• Close parentheses ()) are added if the number of close parentheses is less than the number of open parentheses.

Step-by-Step Breakdown:

1. Start with the empty string"":
   • Add an open parenthesis (.
   • Now you have open = 2 and close = 3.
2. At "(":
   • You still have open = 2 and close = 3 remaining.
   • Add another open parenthesis ( → "((".
   • Now you have open = 1 and close = 3.
3. At "((":
   • Add another open parenthesis ( → "(((".
   • Now you have open = 0 and close = 3.
4. At "(((":
   • No more open parentheses to add (open = 0).
   • Add a close parenthesis ) → "((()".
   • Now you have open = 0 and close = 2.
5. At "((()":
   • Add another close parenthesis ) → "((())".
   • Now you have open = 0 and close = 1.
6. At "((())":
   • Add another close parenthesis ) → "((()))".
   • Now you have open = 0 and close = 0.
   • Since both open and close are 0, the string "((()))" is a valid solution.
7. Backtracking:
   • Backtrack to previous nodes and try other combinations, like adding close parentheses earlier:
     • "(()()", "()(())", "()()()", etc.

Complexity Analysis:

• Time Complexity:
  • The time complexity is proportional to the Catalan numberCn, which is approximately O(4^n / under-root of n).
• Space Complexity:
  • The space complexity is O(n) for the recursion stack since each recursive call adds one level to the stack (up to n levels deep).
  • The result takes up O(4^n / under-root of n) space to store all valid combinations.