Problem Statement
Given a Directed Acyclic Graph of N vertices from 0 to N-1 and M edges and a 2D integer array edges, where there is a directed edge from vertex edge[i][0] to vertex edge[i][1] with a distance of edge[i][2] for all i.
Find the shortest path from source vertex to all the vertices and if it is impossible to reach any vertex, then return -1 for that vertex. The source vertex is assumed to be 0.
Examples
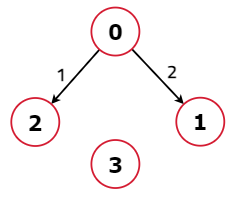
Example 1:
Input: N = 4, M = 2,
edge = [
[0, 1, 2],
[0, 2, 1]
]
Output: 0 2 1 -1
Explanation:
Shortest path from 0 to 1 is 0->1 with edge weight 2.
Shortest path from 0 to 2 is 0->2 with edge weight 1.
There is no way we can reach 3, so it's -1 for 3.Example 2:
Input: N = 6, M = 7,
edge = [
[0, 1, 2],
[0, 4, 1],
[4, 5, 4],
[4, 2, 2],
[1, 2, 3],
[2, 3, 6],
[5, 3, 1]
]
Output: 0 2 3 6 1 5
Explanation:
Shortest path from 0 to 1 is 0->1 with edge weight 2.
Shortest path from 0 to 2 is 0->4->2 with edge weight 1+2=3.
Shortest path from 0 to 3 is 0->4->5->3 with edge weight 1+4+1=6.
Shortest path from 0 to 4 is 0->4 with edge weight 1.
Shortest path from 0 to 5 is 0->4->5 with edge weight 1+4=5.Different Approaches
1️⃣ Topological Sort with Relaxation (BFS)
Approach:
- Step 1: Construct the Graph (Adjacency List)
- Goal: Convert the given list of edges into an adjacency list for easier traversal.
- Intuition: For each vertex, we need to know all its outgoing edges and associated weights.
- Step 2: Compute the In-Degree of Each Vertex
- Goal: count the number of incoming edges for every vertex.
- Intuition: Vertices with an in-degree of 0 have no prerequisites and are the starting points for topological sorting.
- Step 3: Perform a BFS-Based Topological Sort (Kahn's Algorithm)
- Goal: Generate a topological order of vertices.
- Intuition: Process vertices in an order where all dependencies (incoming edges) have been handled.
- Process:
- Enqueue all vertices with in-degree 0.
- Dequeue one vertex at a time and reduce the in-degree of its neighbors.
- Enqueue neighbors whose in-degree becomes 0.
- Step 4: Initialize Distance Array and Set the Source
- Goal: Set the initial distance from the source vertex (0) to all vertices.
- Intuition: The distance to the source is 0, every other vertex starts with an "infinite” distance (here,
INT_MAX).
- Step 5: Relax the Edges in Topological Order
- Goal: Update the shortest distances by relaxing edges.
- Intuition: By processing in topological order, we ensure that when we relax an edge from u to v, the best distance to u is already computed.
- Process:
- For each vertex u in the topological order, update the distance of each neighbor v using:
Code:
class Solution {
public:
vector<int> shortestPath(int N, int M, vector<vector<int>> &edges) {
// Step 1: Construct the Graph using an Adjacency List.
// Each vertex 'u' will have a list of pairs {v, wt} representing a directed edge from u to v with weight wt.
vector<vector<pair<int, int>>> adjList(N);
for (auto edge : edges) {
int u = edge[0];
int v = edge[1];
int wt = edge[2];
adjList[u].push_back({v, wt});
}
// Step 2: Compute the In-Degree of Each Vertex.
// In-degree is the number of incoming edges. This will help us to perform a topological sort.
vector<int> inDegree(N, 0);
for (int i = 0; i < N; i++) {
for (auto itr : adjList[i]) {
inDegree[itr.first]++;
}
}
// Step 3: Perform BFS-Based Topological Sort (Kahn's Algorithm).
// Enqueue all vertices with in-degree 0 (vertices with no prerequisites).
queue<int> que;
for (int i = 0; i < N; i++) {
if (inDegree[i] == 0) {
que.push(i);
}
}
// This vector will store the vertices in topologically sorted order.
vector<int> topoSort;
while (!que.empty()) {
int front = que.front();
que.pop();
topoSort.push_back(front);
// For every adjacent vertex, reduce its in-degree by 1.
// If the in-degree becomes 0, enqueue that vertex.
for (auto itr : adjList[front]) {
inDegree[itr.first]--;
if (inDegree[itr.first] == 0) {
que.push(itr.first);
}
}
}
// Step 4: Initialize the Distance Array.
// Set the distance for the source vertex (vertex 0) to 0 and all other vertices to infinity (INT_MAX).
vector<int> dist(N, INT_MAX);
dist[0] = 0;
// Step 5: Relax the Edges in Topological Order.
// This ensures that when processing a vertex, the shortest path to it is already computed.
for (auto u : topoSort) {
// Only proceed if the current vertex u is reachable from the source.
if (dist[u] != INT_MAX) {
// Check each adjacent vertex from u.
for (auto itr : adjList[u]) {
int v = itr.first; // Destination vertex
int wt = itr.second; // Weight of the edge from u to v
// Relaxation step: update the distance to vertex v if a shorter path is found via u.
if (dist[u] + wt < dist[v]) {
dist[v] = dist[u] + wt;
}
}
}
}
// Step 6: Mark Unreachable Vertices.
// For vertices that are unreachable from the source (distance remains INT_MAX), set the distance to -1.
for (int i = 0; i < N; i++) {
if (dist[i] == INT_MAX) {
dist[i] = -1;
}
}
// Return the final computed shortest path distances.
return dist;
}
};Complexity Analysis:
- Time Complexity:
O(N + M)- Graph Construction:
Building the adjacency list takes O(M) time, where M is the number of edges. - In-Degree Calculation:
Iterating through each vertex's edges to compute the in-degrees also takes O(M) time. - BFS-Based Topological Sort (Kahn's Algorithm):
Each vertex is processed once and each edge is considered once when reducing the in-degrees, contributing O(N+M) time. - Edge Relaxation in Topological Order:
Processing each vertex and relaxing all its outgoing edges takes O(N+M) time. - Final Adjustment:
A simple O(N) pass to update unreachable vertices. - Overall Time Complexity:
O(M)+O(M)+O(N+M)+O(N+M)+O(N)=O(N+M)
Thus, the overall time complexity of the solution is O(N+M).
- Graph Construction:
- Space Complexity:
O(N + M)- Adjacency List:
The graph is stored as an adjacency list, which uses O(M) space since each edge is stored once. - In-Degree Array:
An array of size N is maintained to track the in-degrees of vertices, which requires O(N) space. - Queue for Topological Sort:
The queue used for the BFS-based topological sort may contain up to O(N) vertices in the worst case. - Distance Array:
An array of size N is used to store the shortest path distances, requiring O(N) space. - Overall Space Complexity:
O(M)(adjacency list) + O(N) (in-degree array) + O(N)(queue) + O(N)(distance array) = O(N + M)
- Adjacency List:
2️⃣ Topological Sort with Relaxation (DFS)
Intuition:
Finding the shortest path to a node is easy if the shortest paths to all the nodes that can precede it are known. Processing the nodes in topological order ensures that by the time a node is reached, all the nodes that can precede have already been processed, reducing the computation time significantly.
Thus, for the solution, the nodes will be traversed sequentially according to their reachability from the source.
Once the topological ordering is obtained, all the nodes can be processed one by one. For every vertex being processed, we update the distances of its adjacent using the distance of the current vertex.
Approach:
- The graph is represented using an adjacency list where each node points to its neighboring nodes along with the edge weights.
- Perform a Depth First Search (DFS) to obtain a topological order of the nodes, ensuring each node is processed before its successors.
- Initialize a distance array with a high value (indicating infinity) for all nodes except the source node, which is set to zero.
- Using the topological order, update the shortest distance for each node by relaxing the edges, meaning if a shorter path is found to a neighboring node, update its distance.
- Mark nodes that remain unreachable with a distance of -1. Return the shortest distances from the source to all nodes.
Code:
class Solution {
public:
// DFS helper function to perform a topological sort.
// This function visits all vertices reachable from 'u' and pushes them onto the stack in topologically sorted order.
void dfs(int u, vector<bool>& visited, stack<int>& st, vector<vector<pair<int, int>>>& adjList) {
visited[u] = true; // Mark current vertex as visited
// Explore all outgoing edges from vertex u.
for (auto &edge : adjList[u]) {
int v = edge.first;
if (!visited[v]) {
dfs(v, visited, st, adjList); // Recursively visit unvisited neighbors
}
}
// After exploring all neighbors, push the current vertex onto the stack.
// This ensures that all vertices reachable from u come before u in the stack.
st.push(u);
}
// Main function to compute shortest paths from vertex 0.
vector<int> shortestPath(int N, int M, vector<vector<int>> &edges) {
// Step 1: Construct the Graph using an Adjacency List.
// Each vertex 'u' will have a list of pairs {v, wt} representing an edge from u to v with weight wt.
vector<vector<pair<int, int>>> adjList(N);
for (auto &edge : edges) {
int u = edge[0];
int v = edge[1];
int wt = edge[2];
adjList[u].push_back({v, wt});
}
// Step 2: Perform DFS-based Topological Sort.
// We'll use a stack to store the topological order.
stack<int> st;
vector<bool> visited(N, false);
// Call DFS for each vertex to ensure that we cover the entire graph (even if it's not fully connected).
for (int i = 0; i < N; i++) {
if (!visited[i]) {
dfs(i, visited, st, adjList);
}
}
// Step 3: Initialize the Distance Array.
// Set the distance to the source (vertex 0) as 0, and to all other vertices as infinity (INT_MAX).
vector<int> dist(N, INT_MAX);
dist[0] = 0;
// Step 4: Relax the edges in topological order.
// Process vertices from the top of the stack (which gives us the correct topological order).
while (!st.empty()) {
int u = st.top();
st.pop();
// Only relax if vertex u is reachable from the source.
if (dist[u] != INT_MAX) {
// For every outgoing edge (u -> v) with weight wt, update the distance to v if a shorter path is found.
for (auto &edge : adjList[u]) {
int v = edge.first;
int wt = edge.second;
if (dist[u] + wt < dist[v]) {
dist[v] = dist[u] + wt;
}
}
}
}
// Step 5: Handle Unreachable Vertices.
// Replace any distance that remains as INT_MAX with -1, indicating that the vertex is unreachable from the source.
for (int i = 0; i < N; i++) {
if (dist[i] == INT_MAX) {
dist[i] = -1;
}
}
// Return the computed shortest path distances.
return dist;
}
};Complexity Analysis:
- Time Complexity: O(N+M)
- Topological Sorting takes O(N+M) time.
- To relax all the vertices, each node and its adjacent nodes are traversed taking O(M) time.
- Space Complexity: O(N+M)
- Storing the graph takes O(M) space.
- The stack storing the topological ordering takes O(N) space.
- The topological sorting algorithm uses O(N) space due to visited array and recursion stack space.
