Understanding the Problem

The task at hand is to reverse a singly linked list. Given a linked list, where each node points to the next node in the sequence, the goal is to reverse the direction of these pointers.

Examples

Example 1:

Let's consider we have a linked list as follows:

1->2->3->4

This reverse of this linked list would be as:
4->3->2->1

1️⃣ Brute Force Approach

In this approach, we utilize a stack data structure to store the nodes of the linked list in reverse order. We traverse the list, pushing each node onto the stack. Then, we pop the nodes from the stack and rearrange their pointers to form the reversed linked list.

Algorithm:

1. Create an empty stack. This stack will be used to temporarily store the nodes from the original linked list as we traverse it.
2. Traverse the linked list from head until it is null
   1. Push each node onto the stack.
3. Once all nodes are pushed onto the stack, the stack will contain the nodes of the linked list in reverse order.
4. Again, traverse the linked list.
   1. For every node, pop the top element from stack.
   2. Replace the data part of node with the popped element.
5. Return the head.

Code:

#include <iostream>
#include <bits/stdc++.h>

using namespace std;

// Node class represents a
// node in a linked list
class Node {
public:
    // Data stored in the node
    int data;   
    
    // Pointer to the next node in the list
    Node* next;      

    // Constructor with both data and
    // next node as parameters
    Node(int data1, Node* next1) {
        data = data1;
        next = next1;
    }

    // Constructor with only data as a
    // parameter, sets next to nullptr
    Node(int data1) {
        data = data1;
        next = nullptr;
    }
};

// Function to reverse the
// linked list using a stack
Node* reverseLinkedList(Node* head) {
    // Create a temporary pointer
    // to traverse the linked list
    Node* temp = head;  
    
    // Create a stack to temporarily
    // store the data values
    stack<int> st;     

    // Step 1: Push the values of the
    // linked list onto the stack
    while (temp != nullptr) {
        // Push the current node's
        // data onto the stack
        st.push(temp->data); 
        
        // Move to the next node
        // in the linked list
        temp = temp->next;    
    }
    
    // Reset the temporary pointer to
    // the head of the linked list
    temp = head; 
    
    // Step 2: Pop values from the stack
    // and update the linked list
    while (temp != nullptr) {
        // Set the current node's data to
        // the value at the top of the stack
        temp->data = st.top();  
        
        // Pop the top element from the stack
        st.pop();              
        
        // Move to the next node
        // in the linked list
        temp = temp->next;     
    }
    
    // Return the new head of
    // the reversed linked list
    return head;  
}

// Function to print the linked list
void printLinkedList(Node* head) {
    Node* temp = head;
    while (temp != nullptr) {
        cout << temp->data << " ";
        temp = temp->next;
    }
    cout << endl;
}

int main() {
    // Create a linked list with
    // values 1, 3, 2, and 4
    Node* head = new Node(1);
    head->next = new Node(3);
    head->next->next = new Node(2);
    head->next->next->next = new Node(4);

    // Print the original linked list
    cout << "Original Linked List: ";
    printLinkedList(head);

    // Reverse the linked list
    head = reverseLinkedList(head);

    // Print the reversed linked list
    cout << "Reversed Linked List: ";
    printLinkedList(head);

    return 0;
}

// Output
Original Linked List: 1 3 2 4 
Reversed Linked List: 4 2 3 1 

Complexity Analysis:

• Time Complexity: O(2n)
  • This is because we traverse the linked list twice: once to push the values onto the stack, and once to pop the values and update the linked list.
  • Both traversals take O(n) time, hence time complexity O(2n) ~ O(n).
• Space Complexity: O(n)
  • We use a stack to store the values of the linked list, and in the worst case, the stack will have all n values, i.e., storing the complete linked list.

2️⃣ Iterative Approach:

The iterative approach involves iterating through the linked list and changing the next pointers to reverse the direction. This algorithm has a time complexity of O(n) where n is the number of nodes in the list.

Visual Representation:

Initialization

previous = nullptr
forward = nullptr

-----------     -----      -----      -----      -----      -----
| nullptr |     | 1 |  ->  | 2 |  ->  | 3 |  ->  | 4 |  ->  | 5 |  -> nullptr
----------      -----      -----      -----      -----      -----
    ^             ^
    |             |
previous        current
forward

Iteration 1:

previous = nullptr
forward = nullptr

-----------     -----      -----      -----      -----      -----
| nullptr | <-- | 1 |      | 2 |  ->  | 3 |  ->  | 4 |  ->  | 5 |  -> nullptr
----------      -----      -----      -----      -----      -----
                  ^          ^
                  |          |
               previous   forward | current

previous = 1
forward = 2
current = 2

Iteration 2:

previous = nullptr
forward = 2

-----------     -----      -----      -----      -----      -----
| nullptr | <-- | 1 |  <-- | 2 |      | 3 |  ->  | 4 |  ->  | 5 |  -> nullptr
----------      -----      -----      -----      -----      -----
                             ^          ^
                             |          |
                          previous   forward | current

previous = 2
forward = 3
current = 3

Iteration 3:

previous = 2
forward = 3

-----------     -----      -----      -----      -----      -----
| nullptr | <-- | 1 |  <-- | 2 |  <-- | 3 |      | 4 |  ->  | 5 | -> nullptr
----------      -----      -----      -----      -----      -----
                                        ^          ^
                                        |          |
                                     previous   forward | current

previous = 3
forward = 4
current = 4

Iteration 4:

previous = 3
forward = 4

-----------     -----      -----      -----      -----      -----
| nullptr | <-- | 1 |  <-- | 2 |  <-- | 3 |  <-- | 4 |      | 5 | -> nullptr
----------      -----      -----      -----      -----      -----
                                                   ^          ^
                                                   |          |
                                                previous   forward | current

previous = 4
forward = 5
current = 5

Iteration 5:

previous = 4
forward = 4

-----------     -----      -----      -----      -----      -----
| nullptr | <-- | 1 |  <-- | 2 |  <-- | 3 |  <-- | 4 |  <-- | 5 | -> nullptr
----------      -----      -----      -----      -----      -----
                                                              ^         ^
                                                              |         |
                                                          previous    forward
                                      		           			      current

previous = 5
forward = nullptr
current = nullptr

Since current becomes nullptr, so we break the loop,
and return previous which points to the first item
in reversed list.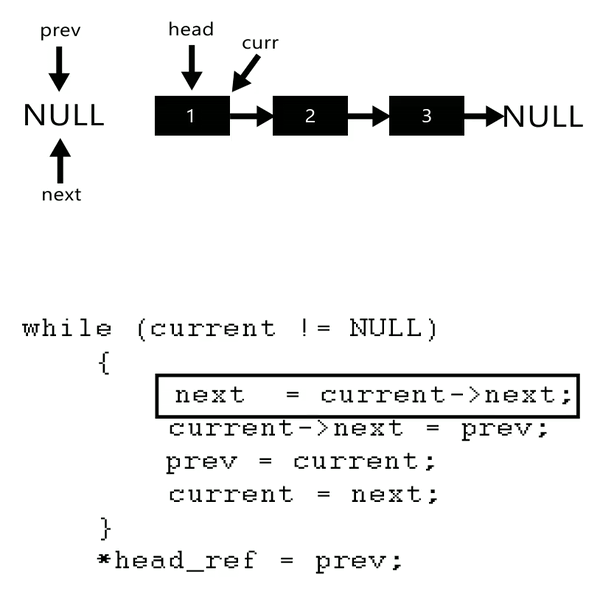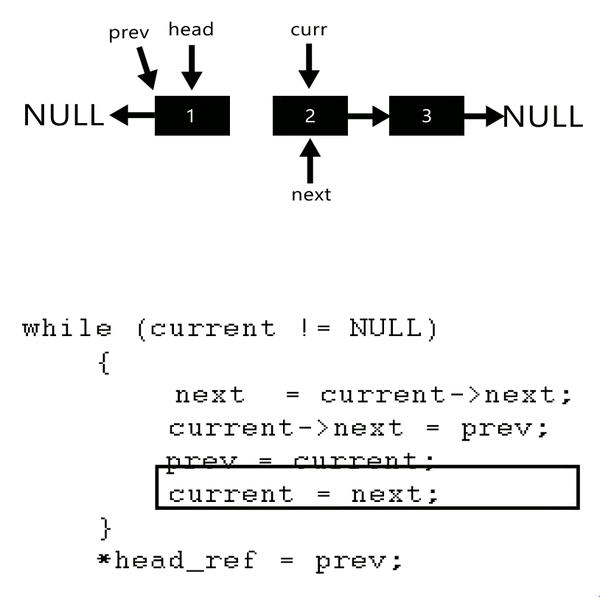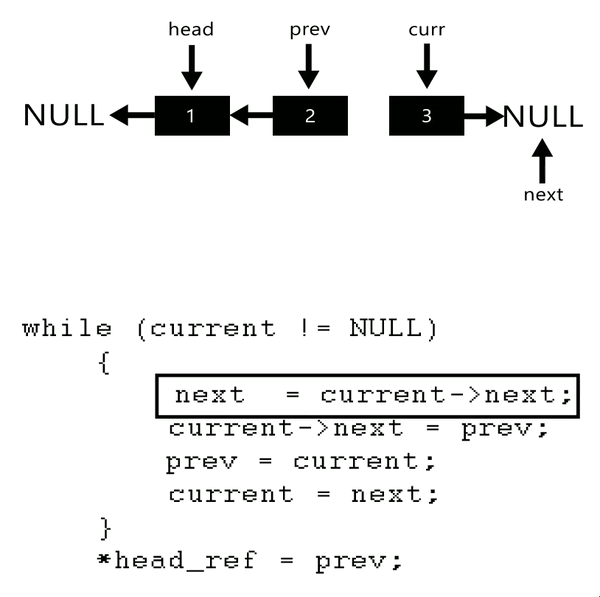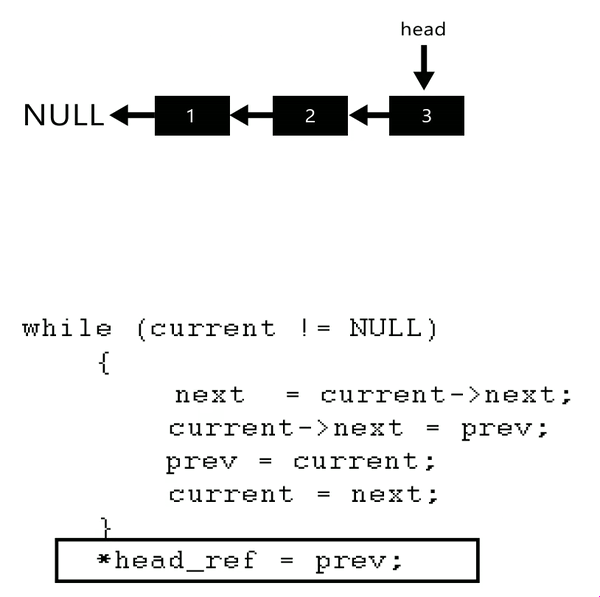

Working Principle:

1. Initialize three pointers: current, prev, and next.
2. Set prev to nullptr, indicating the end of the reversed list.
3. Set current to the head of the original list.
4. While current is not nullptr, repeat the following steps:
   1. Set front to current->next.
   2. Set current->next to to point to prev node.
   3. Move the prev pointer to current node.
   4. Move the current pointer to point to front node.
5. At the end, update the head to the last node and return it.

C++ Implementation:

#include <iostream>

// Define the Node structure
struct Node {
    int data;
    Node* next;
    Node(int val) : data(val), next(nullptr) {}
};

// Function to print the linked list
void printList(Node* head) {
    while (head != nullptr) {
        std::cout << head->data << " ";
        head = head->next;
    }
    std::cout << std::endl;
}

// Iterative approach to reverse a linked list
Node* reverseListIterative(Node* head) {
    Node* current = head;
    Node* prev = nullptr;
    Node* next = nullptr;

    while (current != nullptr) {
        next = current->next;   // Save the next node
        current->next = prev;   // Reverse the link
        prev = current;         // Move to the next pair
        current = next;         // Move to the next pair
    }

    head = prev;  // Update the head to the last node
    return head;
}

int main() {
    // Create a sample linked list: 1 -> 2 -> 3 -> 4 -> 5
    Node* head = new Node(1);
    head->next = new Node(2);
    head->next->next = new Node(3);
    head->next->next->next = new Node(4);
    head->next->next->next->next = new Node(5);

    std::cout << "Original Linked List: ";
    printList(head);

    // Reverse the linked list using the iterative approach
    head = reverseListIterative(head);
    std::cout << "Reversed Linked List (Iterative): ";
    printList(head);

    // Clean up the allocated memory
    while (head != nullptr) {
        Node* temp = head;
        head = head->next;
        delete temp;
    }

    return 0;
}

// Output
Original Linked List: 1 3 2 4 
Reversed Linked List: 4 2 3 1 

Complexity Analysis:

• Time Complexity: O(n)
  • The code traverses the entire linked list once, where n is the number of nodes in the list.
• Space Complexity: O(1)
  • The code uses only a constant amount of additional space, regardless of the linked list's length.

3️⃣ Recursive Approach

The key idea in the recursive approach is to solve a smaller problem first and use its result to solve the bigger problem. We can think of the linked list as being divided into two parts:

1. The head node.
2. The rest of the list.

To reverse the linked list recursively:

1. We start by reversing the sub-list that comes after the head.
2. Once the sub-list is reversed, we adjust the pointers of the head node to complete the reversal.

Working Principle:

1. Base Case: If the list is empty (head == NULL) or has only one node (head->next == NULL), return the head. This base case ends the recursion.
2. Recursive Case: For a list with more than one node:
   1. Reverse the sub-list starting from the second node (head->next).
   2. Adjust the pointers so that the head node becomes the last node in the reversed sub-list.

Dry Run Steps

Let's break down each step of the recursion with the linked list 1 -> 2 -> 3 -> 4 -> 5 -> NULL:

1. First Call: reverseListRecursive(1)
   • Current head: 1
   • List: 1 -> 2 -> 3 -> 4 -> 5 -> NULL
   • Condition Check: head is not NULL, and head->next is not NULL, so we proceed to the recursive call.
   • Recursive Call: reverseListRecursive(2)
2. Second Call: reverseListRecursive(2)
   • Current head: 2
   • List: 2 -> 3 -> 4 -> 5 -> NULL
   • Condition Check: head is not NULL, and head->next is not NULL, so we proceed to the recursive call.
   • Recursive Call: reverseListRecursive(3)
3. Third Call: reverseListRecursive(3)
   • Current head: 3
   • List: 3 -> 4 -> 5 -> NULL
   • Condition Check: head is not NULL, and head->next is not NULL, so we proceed to the recursive call.
   • Recursive Call: reverseListRecursive(4)
4. Fourth Call: reverseListRecursive(4)
   • Current head: 4
   • List: 4 -> 5 -> NULL
   • Condition Check: head is not NULL, and head->next is not NULL, so we proceed to the recursive call.
   • Recursive Call: reverseListRecursive(5)
5. Fifth Call: reverseListRecursive(5)
   • Current head: 5
   • List: 5 -> NULL
   • Condition Check: head is not NULL, but head->next is NULL. This is our base case.
   • Return: The function returns 5.

Unwinding the Recursion

Now, we will start unwinding the recursive calls:

6. Returning to Fourth Call (reverseListRecursive(4)):
   • Reversed Head: 5 (returned from the fifth call)
   • Current head: 4
   • List Before Reversal: 4 -> 5 -> NULL
   • Adjust Pointers:
     • head->next->next = head: 5->next = 4 (now 5 -> 4)
     • head->next = NULL: 4->next = NULL (now 4 -> NULL)
   • List After Reversal: 5 -> 4 -> NULL
   • Return: 5 (new head of the reversed sublist)
7. Returning to Third Call (reverseListRecursive(3)):
   • Reversed Head: 5 (returned from the fourth call)
   • Current head: 3
   • List Before Reversal: 3 -> 4 -> NULL (with 5 -> 4)
   • Adjust Pointers:
     • head->next->next = head: 4->next = 3 (now 5 -> 4 -> 3)
     • head->next = NULL: 3->next = NULL (now 3 -> NULL)
   • List After Reversal: 5 -> 4 -> 3 -> NULL
   • Return: 5 (new head of the reversed sublist)
8. Returning to Second Call (reverseListRecursive(2)):
   • Reversed Head: 5 (returned from the third call)
   • Current head: 2
   • List Before Reversal: 2 -> 3 -> NULL (with 5 -> 4 -> 3)
   • Adjust Pointers:
     • head->next->next = head: 3->next = 2 (now 5 -> 4 -> 3 -> 2)
     • head->next = NULL: 2->next = NULL (now 2 -> NULL)
   • List After Reversal: 5 -> 4 -> 3 -> 2 -> NULL
   • Return: 5 (new head of the reversed sublist)
9. Returning to First Call (reverseListRecursive(1)):
   • Reversed Head: 5 (returned from the second call)
   • Current head: 1
   • List Before Reversal: 1 -> 2 -> NULL (with 5 -> 4 -> 3 -> 2)
   • Adjust Pointers:
     • head->next->next = head: 2->next = 1 (now 5 -> 4 -> 3 -> 2 -> 1)
     • head->next = NULL: 1->next = NULL (now 1 -> NULL)
   • List After Reversal: 5 -> 4 -> 3 -> 2 -> 1 -> NULL
   • Return: 5 (new head of the fully reversed list)

5 -> 4 -> 3 -> 2 -> 1 -> NULL

C++ Implementation:

#include <iostream>
#include <bits/stdc++.h>

using namespace std;

// Node class represents a
// node in a linked list
class Node {
public:
    // Data stored in the node
    int data;   
    
    // Pointer to the next node in the list
    Node* next;      

    // Constructor with both data and
    // next node as parameters
    Node(int data1, Node* next1) {
        data = data1;
        next = next1;
    }

    // Constructor with only data as a
    // parameter, sets next to nullptr
    Node(int data1) {
        data = data1;
        next = nullptr;
    }
};

// Function to reverse a singly
// linked list using a recursion

Node* reverseLinkedList(Node* head) {
    // Base case:
    // If the linked list is empty or has only one node,
    // return the head as it is already reversed.
    if (head == NULL || head->next == NULL) {
        return head;
    }
    
    // Recursive step:
    // Reverse the linked list starting 
    // from the second node (head->next).
    Node* newHead = reverseLinkedList(head->next);
    
    // Save a reference to the node following
    // the current 'head' node.
    Node* front = head->next;
    
    // Make the 'front' node point to the current
    // 'head' node in the reversed order.
    front->next = head;
    
    // Break the link from the current 'head' node
    // to the 'front' node to avoid cycles.
    head->next = NULL;
    
    // Return the 'newHead,' which is the new
    // head of the reversed linked list.
    return newHead;
}


// Function to print the linked list
void printLinkedList(Node* head) {
    Node* temp = head;
    while (temp != nullptr) {
        cout << temp->data << " ";
        temp = temp->next;
    }
    cout << endl;
}

int main() {
    // Create a linked list with
    // values 1, 3, 2, and 4
    Node* head = new Node(1);
    head->next = new Node(3);
    head->next->next = new Node(2);
    head->next->next->next = new Node(4);

    // Print the original linked list
    cout << "Original Linked List: ";
    printLinkedList(head);

    // Reverse the linked list
    head = reverseLinkedList(head);

    // Print the reversed linked list
    cout << "Reversed Linked List: ";
    printLinkedList(head);

    return 0;
}

// Output
Original Linked List: 1 3 2 4 
Reversed Linked List: 4 2 3 1 

Complexity Analysis:

• Time Complexity: O(n)
  • Linear, where n is the number of nodes.
• Space Complexity: O(n)
  • Linear, due to the recursive call stack.