When Prefix Sum Falls Short: Enter the Fenwick Tree

When solving problem involving array sums, the prefix sum technique is often the first tool we reach for.  It's simple, intuitive, and works perfectly in scenarios where we need to calculate the sum of elements from the start of the array up to a specific index. Bu what happens when the problem involves updates to the array? Here, the prefix sum struggles, and this is where the Fenwick Tree (Binary Indexed Tree) becomes a game-changer.

The Prefix Sum Approach

Let's start with a common scenario where prefix sum excel:

Problem Statement:

Given an array arrof size n, answer multiple queries of the form:

• Find the sum of elements from index 1to i(1-based index).

Solution Using Prefix Sum:

We precompute the prefix sums in an auxiliary array prefix, where:

prefix[i] = arr[1] + arr[2] + ... + arr[i]

Using this array, the sum of elements from index 1 to i can be computed in O(1) as:

prefix[i]

:

prefix[i] = arr[1] + arr[2] + ... + arr[i]

Using this array, the sum of elements from index 1to ican be computed in O(1) as:

prefix[i]

Example:

      +-----+-----+-----+-----+-----+
arr = |  1  |  2  |  3  |  4  |  5  |
      +-----+-----+-----+-----+-----+
         0     1     2     3     4
                 +-----+-----+-----+-----+-----+
precomputation = |  1  |  3  |  6  | 10  | 15  |
                 +-----+-----+-----+-----+-----+
                    0     1     2    3      4

We can now easily find the sum of any range using the precomputation array:
Suppose we need to find the sum of subarray from 1 to 3
sum(L, R) = precomputation[R] - precomputation[L - 1]
It would be precomputation[3] - precomputation[0]
10 - 1 = 9;

Efficiency:

• Precomputing the prefix sum array takes O(n).
• Answering each query takes O(1).

This is fast and efficient for static arrays where the values don’t change. But what if the array is dynamic?

When Updates Enter the Picture

Extended Problem Statement:

Now consider the same problem, but with an additional operation:

• Update the value at a specific index.

For example, update arr[k] = x, After this update, any future prefix sum queries must reflect the change.

      +-----+-----+-----+-----+-----+
arr = |  1  |  2  |  3  |  4  |  5  |
      +-----+-----+-----+-----+-----+
         0     1     2     3     4
                 +-----+-----+-----+-----+-----+
precomputation = |  1  |  3  |  6  | 10  | 15  |
                 +-----+-----+-----+-----+-----+
                    0     1     2    3      4
                    
Suppose we are told to update the val at index 2 of arr with 5.
So in this case we need to update the precomputation array from that
particular index and after it.
      +-----+-----+-----+-----+-----+
arr = |  1  |  2  |  5  |  4  |  5  |
      +-----+-----+-----+-----+-----+
         0     1     2     3     4
         
Find out the difference of the old value and new value at index 2.
old value = 3
new value = 5
difference = 5 - 3 = 2
So add this difference at index 2 of precomputation array and all subsequent indexes.
such that it becomes:

                 +-----+-----+-----+-----+-----+
precomputation = |  1  |  3  |  8  | 12  | 17  |
                 +-----+-----+-----+-----+-----+
                    0     1     2    3      4
So if there is updation at index 0, so we have to update whole precomputation prefix array, which takes O(n) time.

So to reduce this O(n) time, we use Fenwick Tree.
Fenwick Tree reduces it to O(log n).

Why Prefix Sum Fails:

If we use the prefix sum array, every update requires re-computing all prefix sums for indices greater than or equal to k. This operation takes O(n), making updates highly inefficient when there are many of them.

Enter the Fenwick Tree:

The Fenwick Tree solves this problem by allowing both prefix sum queries and updates to be performed efficiently in O(log n) time. It achieves this by storing partial sums in a tree-like structure (though it's implemented as a flat array).

Key Operations in Fenwick Tree:

1 Update Operation:

• When you update an element in the array, the Fenwick Tree updates only the necessary partial sums, avoiding the need to recompute the entire prefix sum array.

2 Query Operation:

• To compute the prefix sum, the Fenwick Tree efficiently combines the relevant partial sums.

Efficiency:

• Both updates and prefix sum queries take O(log n) time.

Example: Solving the Problem with Fenwick Tree

Let's revisit the earlier problem and solve it using a Fenwick Tree.

Problem:

Given an array arrof size n, perform the following operations:

1. Update the value at index ito x.
2. Query the sum of elements from index 1to i.

Fenwick Tree Solution:

We use an auxiliary array bit[](Binary Indexed Tree) of size n+1(1-based indexing) to store partial sums.

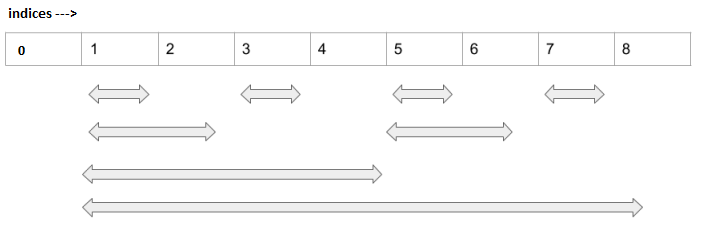
Step 1: Initialization

Initialize the bitarray to 0. We will update it as we process the array.

Step 2: Update Operation

To update the value at index iby delta(difference between the new and old values), we:

• Add deltato bit[i].

• Propagate the change to subsequent indices using the formula:

  i = i + (i & -i)

Step 3: Query Operation

To find the prefix sum from index 1to i, we:

• Sum up the values in bit[i]and move to the parent index using the formula:

  i = i - (i & -i)

Let's illustrate this with an example:

Input: arr = [0, 5, 3, 7, 9, 6] (1-based index)

1 Build the Fenwick Tree:

Initially, it would be initialized to 0.

bit = [0, 0, 0, 0, 0, 0]

• For arr[1] = 5, update bit.
• Repeat for all elements

2 Query and Update:

• Query: Find the sum from 1to 4. The result is computed using bitvalues.
• Update: Change arr[3]from 7to 10. Update the bitarray to reflect this change.

Step by Step Understanding

Fenwick Tree (or Binary Indexed Tree) is a data structure that efficiently supports prefix sum queries and updates on an array. It's widely used for scenarios where frequent cumulative sum queries and updates are needed.

Key Concepts:

• Purpose: Quickly compute the prefix sum (sum of elements from the start to a given index) and update individual elements in an array.
• Efficiency: Both operations (query and update) have a time complexity of O(log n).

Structure

The Fenwick Tree is based on the binary representation of indices. Each node in the tree stores a cumulative sum of elements in a specific range, determined by the position of the least significant bit (LSB) of the index.

Operations

1. Building the Tree: Initialize all elements of the tree to 0 and update it for each array element.
2. Update: Modify the value of an element and propagate the changes to relevant nodes.
3. Query: Compute the prefix sum by traversing the tree from the given index toward the root.

Code for Fenwick Tree

#include <iostream>
#include <vector>
using namespace std;

class FenwickTree {
private:
    vector<int> BIT; // Fenwick Tree array
    int n;           // Size of the array

public:
    FenwickTree(int size) {
        n = size;
        BIT.resize(n + 1, 0); // Initialize with 0
    }

    // Point Update: Add 'value' to index 'i'
    void update(int i, int value) {
        while (i <= n) {
            BIT[i] += value;
            i += (i & -i); // Move to the next index
        }
    }

    // Query: Get the sum from 1 to 'i'
    int query(int i) {
        int sum = 0;
        while (i > 0) {
            sum += BIT[i];
            i -= (i & -i); // Move to the parent index
        }
        return sum;
    }

    // Range Query: Get the sum from 'l' to 'r'
    int rangeQuery(int l, int r) {
        return query(r) - query(l - 1);
    }
};

int main() {
    int n = 10; // Example array size
    FenwickTree ft(n);

    // Example: Update array values
    ft.update(1, 3);  // Add 3 to index 1
    ft.update(4, 5);  // Add 5 to index 4
    ft.update(7, 2);  // Add 2 to index 7

    // Example: Query
    cout << "Sum from 1 to 5: " << ft.query(5) << endl;    // Output: 8
    cout << "Sum from 1 to 10: " << ft.query(10) << endl;  // Output: 10

    // Range Query
    cout << "Sum from 4 to 7: " << ft.rangeQuery(4, 7) << endl; // Output: 7

    return 0;
}

Uses:

Fenwick Tree is used for following problems:

1. Range Sum = You have to find the sum of elements in the range
2. Range Max Query = You have to find the max element in the range
3. Range Min Query = You have to find the min element in the range
4. Range XOR = You have to do XOR operations in a range