Problem Statement

Given a string s, write a program to return all possible permutations of the characters in the string. Each permutation should be a distinct arrangement of the characters in s. If the string contains duplicate characters, ensure that the output does not contain duplicate permutations.

Constraints:

1. The input string s may contain duplicate characters.
2. The output should include only unique permutations.

Input:

• A string s consisting of lowercase/uppercase English letters or digits.

Output:

• A list of strings containing all unique permutations of the characters in s.

Examples

Example 1:

Input: "abc"
Output: [
         "abc",
         "acb",
         "bac",
         "bca",
         "cab",
         "cba"
        ]

Explanation:
 +---+---+---+
 |   |   |   |
 +---+---+---+

In First block, we can place all three characters.
In Second block, we only have two choices.
In Third block, we only have one left choice.

So total outcomes = 3 * 2 * 1 = 3!
                  = n! (where n is input.size())
                  = 3! = 3*2 = 6

Example 2:

Input: "0, 1"
Output: [
         "0, 1",
         "1, 0"
        ]

Example 3:

Input: "aab"
Output: [
         "aab",
         "aba",
         "baa"
        ]

Explanation:
There are only 3 unique permutations since repeating "a"s produce some duplicate arrangements.
Total Permutation (for duplicates) = (number of character)! / (number of repeated character)!
                                   = 3! / 2!
                                   = 3

Different Approaches

Well If the string contains duplicates, how do we handle it:

1. Generate all the permutation, remove the repeated using any data structure like set. However it has the drawback that we did complete work without optimization and used the secondary data structure like set, which do increase the space complexity.
2. The Other way we can use to remove the duplicate from the string and the generate the permutations.
3. The third way is while you are building the recursive tree (generating permutations), when you encounter the same choice in subsequent calls then just crop that branch (don't execute, it is redundant). It is called as controlled recursion.

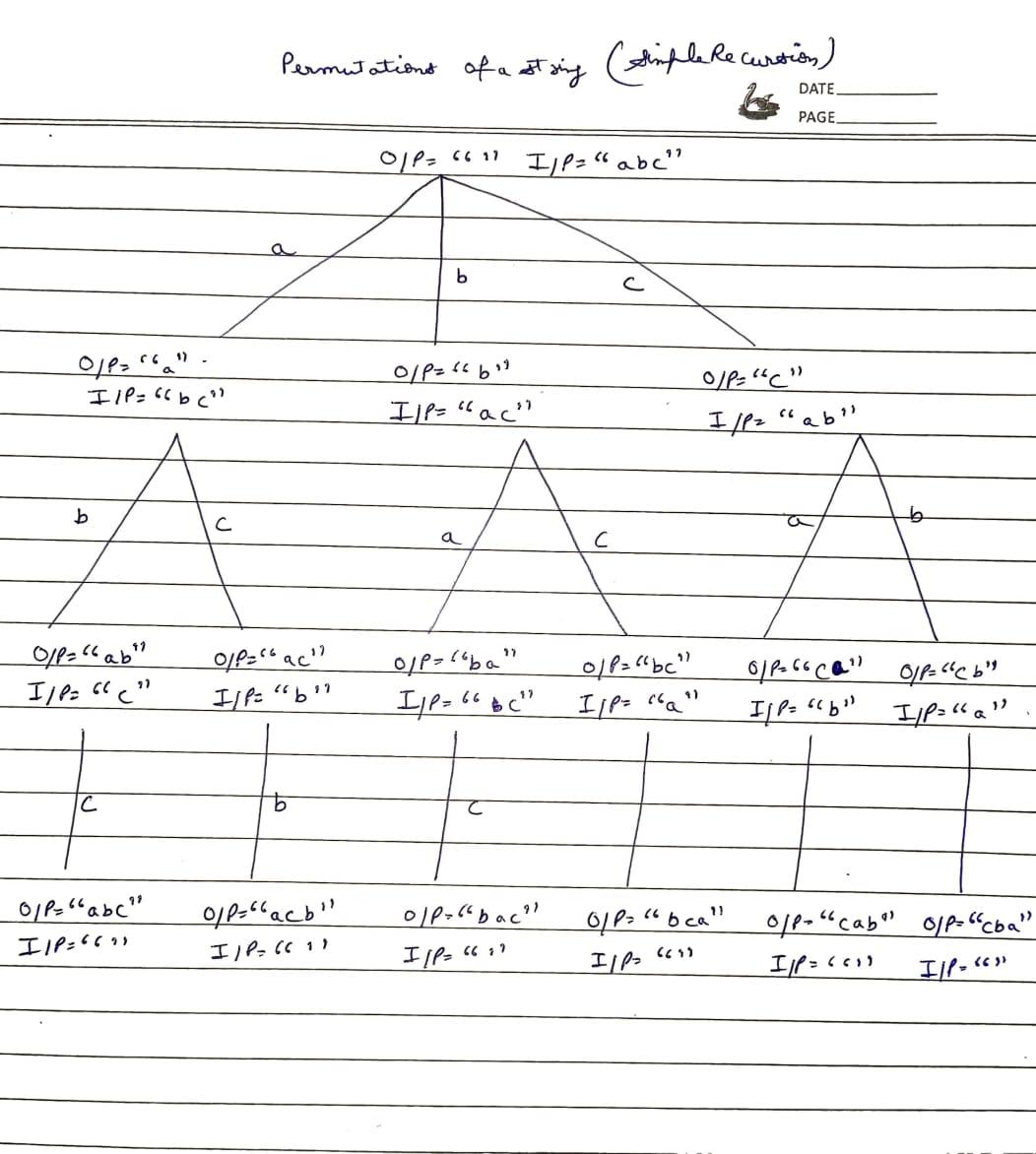
1️⃣ Simple Recursion with Visited Array

Intuition:

We can use a boolean array to track which elements have been used. This approach works well for generating permutations without modifying the original array.

Steps:

1. Create a visited array to track which elements are already included in the current permutation.
2. Recursively add each unused element to the current permutation.
3. After each recursive call, mark the element as unused (backtracking).

Code Which doesn't handle Duplicates:

If there are duplicate elements in nums, the below code will produce duplicate permutations because it treats each element in nums as unique due to lack of a condition to skip duplicates.

#include <iostream>
#include <vector>

using namespace std;


class Solution {
public:
    // Helper function for generating permutations
    void permute(vector<vector<int>>& result, vector<int> &arr, vector<int> &current, vector<bool> &visited) {
        // Base case: if the current permutation has the same size as arr, add it to the result
        if (current.size() == arr.size()) {
            result.push_back(current);
            return;
        }
        // Recursive case: iterate through each element in arr
        for (int i = 0; i < arr.size(); i++) {
            // Check if this element has been visited
            if (!visited[i]) {
                visited[i] = true;              // Mark the element as visited
                current.push_back(arr[i]);      // Add the element to the current permutation
                permute(result, arr, current, visited);  // Recurse with this element added
                current.pop_back();             // Backtrack: remove the last element added
                visited[i] = false;             // Reset the visited status for the element
            }
        }
    }

    // Main function to be called for generating permutations
    vector<vector<int>> permute(vector<int>& nums) {
        vector<vector<int>> result;           // Store all permutations
        vector<int> output;                   // Track current permutation
        vector<bool> visited(nums.size(), false);  // Track visited elements
        permute(result, nums, output, visited);    // Start the recursive permutation generation
        return result;                        // Return all permutations generated
    }
};

Dry Run:

Initialization:

nums = {1, 2, 3}

• We start by calling permute(nums).
• In permute, we initialize:
  • result as an empty vector to store all permutations.
  • output as an empty vector to build each permutation step-by-step.
  • visited as a boolean vector {false, false, false} to track visited elements.
• We call the helper function permute(result, nums, output, visited).

First Call to permute(result, nums, output, visited):

Current State:
    output = {}
    visited = {false, false, false}

Since output.size() != nums.size(), we enter the loop.

Iteration 1 (i = 0)
    visited[0] = true (mark 1 as visited)
    output.push_back(1); output becomes {1}
    Recursive Call: permute(result, nums, output, visited).
    Second Call to permute(result, nums, output, visited):
        Current State:
            output = {1}
            visited = {true, false, false}
        
        We enter the loop since output.size() != nums.size()
        
        Iteration 1 (i = 0):
            visited[1] = true, so we skip to the next iteration.
        Iteration 2 (i = 1):
            visited[1] = true (mark 2 as visited).
            output.push_back(2); output becomes {1, 2}.
            Recursive Call: permute(result, nums, output, visited).
            
            Third Call to permute(result, nums, output, visited):
                Current State:
                    output = {1, 2}
                    visited = {true, true, false}
                We enter the loop since output.size() != nums.size()
                Iteration 1 (i = 0) and Iteration 2 (i = 1):
                    Both visited[0] and visited[1] are true, so we skip to the next iteration.
                Iteration 3 (i = 2):
                    visited[2] = true (mark 3 as visited).
                    output.push_back(3); output becomes {1, 2, 3}.
                    Recursive Call: permute(result, nums, output, visited).
                
                    Fourth Call to permute(result, nums, output, visited)
                    Current State:
                        output = {1, 2, 3}
                        visited = [true, true, true}
                    
                        Now output.size() == nums.size(), so we have a complete permutation.
                        result.push_back(output) adds {1, 2, 3} to result.
                    Backtracking:
                        output.pop_back() removes 3, making output = {1, 2}
                        visited[2] = false (unmark 3 as visited.)
                    Return to the previous call.
            
                Back to Third Call:
                    State after Backtracking:
                        output = {1, 2}
                        visited = {true, true, false}
                    The loop completes, so we backtrack further:
                        output.pop_back() removes 2, making output = {1}.
                        visited[1] = false (unmark 2 as visited).
                
        Back to Second Call:
        Iteration 3 (i = 2)
            visited[2] = true (mark 3 as visited).
            output.push_back(3); output becomes {1, 3}.
            Recursive Call: permute(result, nums, output, visited).
            
            ... and so on.

Code which Handles the Duplicates:

To handle the duplicates, you can sort the array first and then add a condition to skip duplicate elements during the permutation generation.

1. Sort the input array: This ensures that duplicates are adjacent, making it easier to skip them.
2. Skip Duplicates: Add a check to skip an element if it's the same as the previous one and the previous element was not used in the current recursive path.

class Solution {
public:
    // Helper function to generate permutations while skipping duplicates
    void permute(vector<vector<int>>& result, vector<int> &arr, vector<int> &current, vector<bool> &visited) {
        if (current.size() == arr.size()) {
            result.push_back(current);
            return;
        }
        for (int i = 0; i < arr.size(); i++) {
            // Skip if element is already used or if it is a duplicate of the previous element
            // that hasn't been used in this recursive path
            if (visited[i] || (i > 0 && arr[i] == arr[i - 1] && !visited[i - 1])) {
                continue;
            }
            visited[i] = true;                // Mark as visited
            current.push_back(arr[i]);        // Add element to current permutation
            permute(result, arr, current, visited); // Recurse
            current.pop_back();               // Backtrack
            visited[i] = false;               // Unmark as visited
        }
    }

    vector<vector<int>> permuteUnique(vector<int>& nums) {
        vector<vector<int>> result;
        vector<int> output;
        vector<bool> visited(nums.size(), false);

        // Sort to handle duplicates by positioning them adjacent
        sort(nums.begin(), nums.end());
        permute(result, nums, output, visited);
        return result;
    }
};

Dry Run:

Initialization:

nums = {1, 1, 2}

Call permuteUnique(nums).
Inside permuteUnique:
    Sort nums, which remains {1, 1, 2} (already sorted).
    Initialize result as an empty vector to store unique permutations.
    output as an empty vector for the current permutation.
    visited as {false, false, false} to track visited elements.
    Call the helper function permute(result, nums, output, visited).

First Call to permute(result, nums, output, visited)

Current State:
    nums = {1, 1, 2}
    output = {}
    visited = {false, false, false}

Since output.size() != nums.size(), we enter the loop.

Iteration 1 (i = 0)
    visited[0] = true (mark the first 1 as visited).
    output.push_back(1); output becomes {1}.
    Recursive Call: permute(result, nums, output, visited).
    
    Second Call to permute(result, nums, output, visited)
        Current State:
            nums = {1, 1, 2}
            output = {1}
            visited = {true, false, false}
        
        We enter the loop since output.size() != nums.size().
        
        Iteration 1 (i = 0)
            visited[0] is true, so we skip this iteration.
        Iteration 2 (i = 1)
            visited[1] = (mark the second 1 as visited).
            output.push_back(1); output becomes {1, 1}.
            Recursive Call: permute(result, nums, output, visited).
            
            Third Call to permute(result, nums, output, visited)
                Current State:
                    nums = {1, 1, 2}
                    output = {1, 1}
                    visited = {true, true, false}
                We enter the loop.
                Iteration 1 (i = 0) and Iteration 2 (i = 1)
                    Both visited[0] and visited[1] are true, so we skip these iterations.
                Iteration 2 (i = 2)
                    visited[2] = true (mark 2 as visited).
                    output.push_back(2); output becomes {1, 1, 2}.
                    Recursive Call: permute(result, nums, output, visited).
                    
                    Fourth Call to permute(result, nums, output, visited)
                        Current State:
                            nums  = {1, 1, 2}
                            output = {1, 1, 2}
                            visited = {true, true, true}
                        Now output.size() == nums.size(), so we add {1, 1, 2} to result.
                        
                        Backtrack:
                            Remove 2 from output, output = {1, 1}.
                            Set visited[2] = false (unmark 2 as visited).
                        Return to previous call.
            Back to Third Call:
                State after Backtracking:
                    output = {1, 1}
                    visited = {true, true, false}
                Loop is complete. We backtrack further:
                    Remove the last 1 from output, making output = {1}
                    Set visited[1] = false

        Iteration 3 (i = 2):
            visited[2] = true (mark 2 as visited).
            output.push_back(2); output becomes {1, 2}
            Recursive Call: permute(reuslt, nums, output, visited)
            
            Fifth Call to permute:
                Current State:
                    nums = {1, 1, 2}
                    output = {1, 2}
                    visited = {true, false, true}
                We enter the loop.
                Iteration 1 (i = 0):
                    Since visited[0] is true, we skip the iteration.
                Iteration 2 (i = 1):
                    visited[1] = true (mark the second 1 as visited).
                    output.push_back(1); output becomes {1, 2, 1}
                    Recursive Call: permute(result, nums, output, visited).
                    
                    Sixth Call to permute:
                        Current State:
                            output: {1, 2, 1}
                            visited: {true, true, true}
                        Now, output.size() == nums.size(), so we add {1, 2, 1} tp result.
                        Backtrack:
                            Remove 1 from output, making output = {1, 2}.
                            Set visited[1] = false.
                Back to Fifth Call and Backtrack furhter:
                    Remove 2 from output, making output = {1}.
                    Set visited[2] = false.
                    Completed the loop, then backtrack to output = {} and visited = {false, false, false}.
                    
                    ... and so on.

Complexity Analysis:

• Time Complexity: O(n * n!)
• Space Complexity: O(n!)

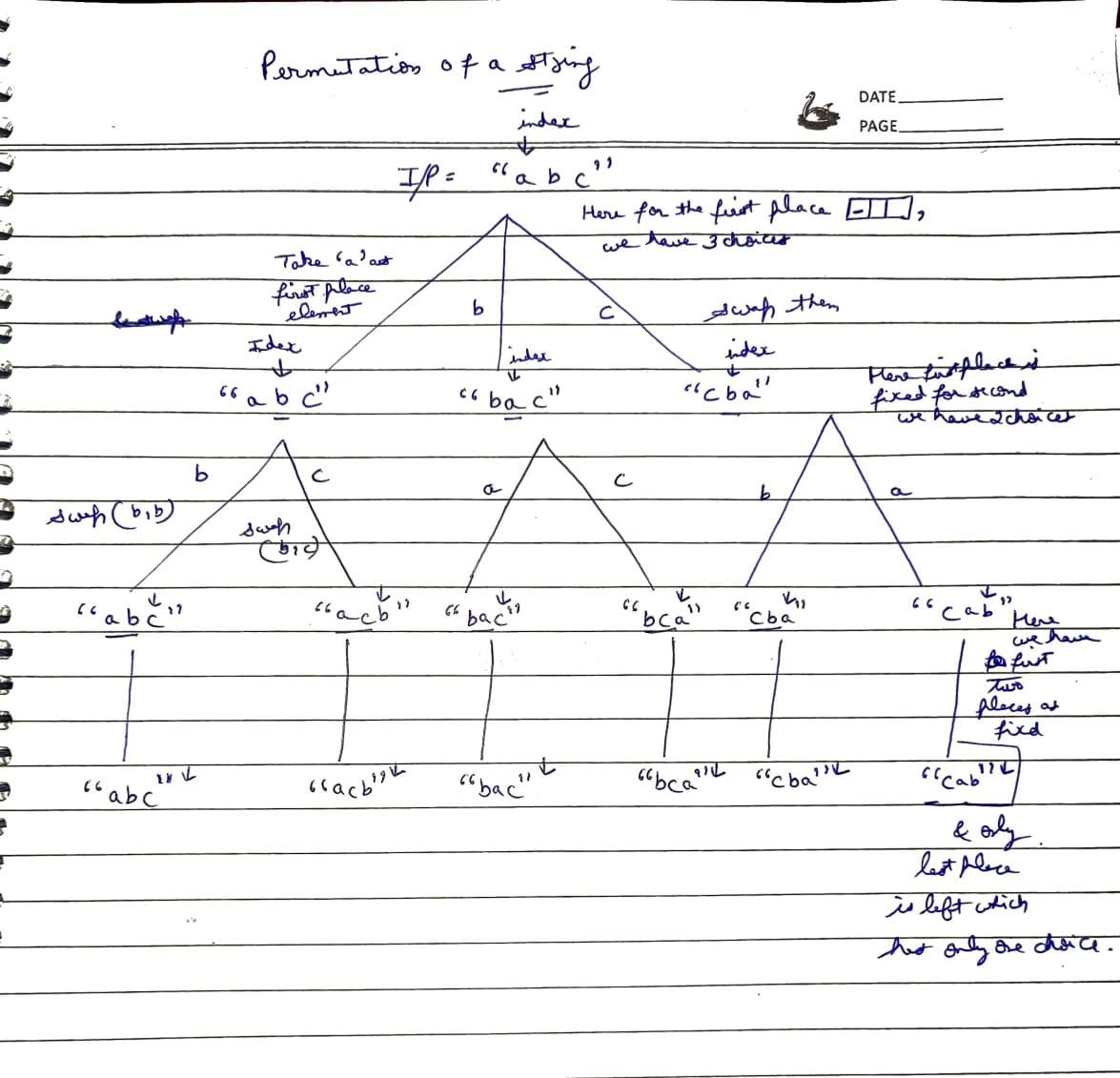
2️⃣ Backtracking (Swap-Based) Approach

This is the most straightforward approach to generating permutations, which involves swapping elements recursively.

Steps:

1. At each recursive level, swap each element with the current position.
2. Recurse to generate permutations for the remaining part of the array.
3. After each recursive call, swap back to restore the original order (backtracking).

Code which Doesn't Handles Duplicates:

#include <iostream>
#include <vector>

class Solution {
public:
    // Main function to generate permutations
    vector<vector<int>> permute(vector<int>& nums) {
        vector<vector<int>> result;             // Stores all permutations
        permuteRec(nums, 0, result);            // Helper function for recursion
        return result;                          // Return the result with all permutations
    }

    // Helper function to generate permutations recursively
    void permuteRec(vector<int>& nums, int currentIndex, vector<vector<int>>& result) {
        // Base case: if the currentIndex is at the last position
        // then nums holds a complete permutation
        if (currentIndex == nums.size() - 1) {
            result.push_back(nums);             // Add current permutation to result
            return;
        }

        //Recurise Case: Loop to iterate through each element and swap it to currentIndex
        for (int index = currentIndex; index < nums.size(); index++) {
            swap(nums[currentIndex], nums[index]);  // Swap to put the current element in position
            permuteRec(nums, currentIndex + 1, result);  // Recurse with the next index element
            swap(nums[currentIndex], nums[index]);  // Backtrack to restore the original order.
        }
    }
};

Code which Handles the Duplicates:

To ensure only unique permutations are generated when duplicates are present, you can use a set to avoid duplicating the same permutation during the swapping process. An alternative approach is to sort the array initially and skip over duplicates by checking if the element has been swapped in the current iteration.

class Solution {
public:
    vector<vector<int>> permuteUnique(vector<int>& nums) {
        vector<vector<int>> result;
        sort(nums.begin(), nums.end());      // Sort to make duplicate checking easier
        permuteRec(nums, 0, result);
        return result;
    }

    void permuteRec(vector<int>& nums, int currentIndex, vector<vector<int>>& result) {
        if (currentIndex == nums.size() - 1) {
            result.push_back(nums);
            return;
        }

        for (int index = currentIndex; index < nums.size(); index++) {
            // Skip duplicates by ensuring the same element isn't used more than once per position
            if (index != currentIndex && nums[index] == nums[currentIndex]) continue;

            swap(nums[currentIndex], nums[index]);           // Swap elements
            permuteRec(nums, currentIndex + 1, result);      // Recurse to the next position
            swap(nums[currentIndex], nums[index]);           // Backtrack
        }
    }
};