Problem Statement

Given a binary tree, the task is to find its maximum depth of the tree. In other words, we need to determine the length of the longest path from the root node to any leaf node in the tree.

Examples

Example 1:

Consider the following binary tree:

     1
    / \
   2   3
      / \
     4   5

The maximum depth of this tree is 3.

Example 2:

         5
        / \
       3   7
      / \
     1   4
        /
       2

The maximum depth of this tree is 4.

Theory

Depth: of a tree refers to the length of the longest path from the root node to a leaf node.

Maximum Depth: of a tree data structure is the length of the longest path from the root node to a leaf node. It represents the furthest distance between the root and any leaf node in the tree.

• The maximum depth of a binary tree is essentially the height of the tree.

Different Approach

1️⃣ Recursive Approach:

Intuition:

To find the maximum height of a binary tree a possible solution is using a recursive approach to divide the tree into smaller sub-trees. By finding the depth of these sub-trees and combining them, determine the depth of the entire tree. For each node in the tree, find the maximum depth of the left and right subtree, take the larger of these two depths, and add one (for the current node).

One of the simplest approaches is to use recursion. We recursively traverse the left and right subtrees, calculating the depth of each subtree and returning the maximum depth among them.

Function maxDepth(root):
    If root is null:
        Return 0
    Else:
        Return 1 + max(maxDepth(root->left), maxDepth(root->right))

Explanation:

• Base Case: If the root node is null (indicating an empty subtree), then the depth of this subtree is 0. We return 0.
• Recursive Case: If the root node is not null, then we compute the depth of the left subtree and the depth of the right subtree recursively. The depth of the current subtree is the maximum depth among these two subtrees plus 1 (to account for the current node). We return this value.

Code:

#include <iostream>
#include <algorithm>

// Definition for a binary tree node.
struct TreeNode {
    int val;
    TreeNode* left;
    TreeNode* right;
    TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
};

// Recursive function to find the maximum depth of the binary tree
int maxDepthRecursive(TreeNode* root) {
    // Base case: If the root is null, the depth is 0
    if (root == nullptr)
        return 0;
    
    // Recursively calculate the depth of the left and right subtrees
    int leftDepth = maxDepthRecursive(root->left);
    int rightDepth = maxDepthRecursive(root->right);
    
    // Return the maximum depth among the left and right subtrees, plus 1 for the current node
    return 1 + std::max(leftDepth, rightDepth);
}

int main() {
    // Example binary tree creation
    TreeNode* root = new TreeNode(1);
    root->left = new TreeNode(2);
    root->right = new TreeNode(3);
    root->right->left = new TreeNode(4);
    root->right->right = new TreeNode(5);

    // Call the recursive function to find the maximum depth
    std::cout << "Maximum Depth of the Binary Tree (Recursive Approach): " << maxDepthRecursive(root) << std::endl;

    return 0;
}

• In the recursive function:
  • We first check if the root is null. If it is, we return 0, indicating that the depth of the subtree rooted at this node is 0.
  • Otherwise, we recursively calculate the maximum depth of the left and right subtrees by calling maxDepthRecursive on the left and right children of the current node.
  • We then return the maximum depth among the left and right subtrees, plus 1 for the current node.

Complexity Analysis:

• Time Complexity: O(N)
  • In the worst-case scenario, where the binary tree is completely unbalanced (skewed), the time complexity of the recursive approach is O(N), where N is the number of nodes in the tree. This is because the algorithm visits each node exactly once.
  • In the average case or when the tree is balanced, the time complexity is still O(N), where N is the number of nodes.
• Space Complexity: O(h), where h is the height of the tree.
  • The space complexity of the recursive approach is determined by the recursive calls on the call stack. In the worst-case scenario, the depth of the call stack can be equal to the height of the binary tree.
  • In a balanced binary tree, the height of the tree is approximately log(N), where N is the number of nodes. Therefore, the space complexity is O(log N).
  • In an unbalanced binary tree, the height of the tree can be equal to N, leading to a space complexity of O(N).

2️⃣ Iterative Approach:

Intuition:

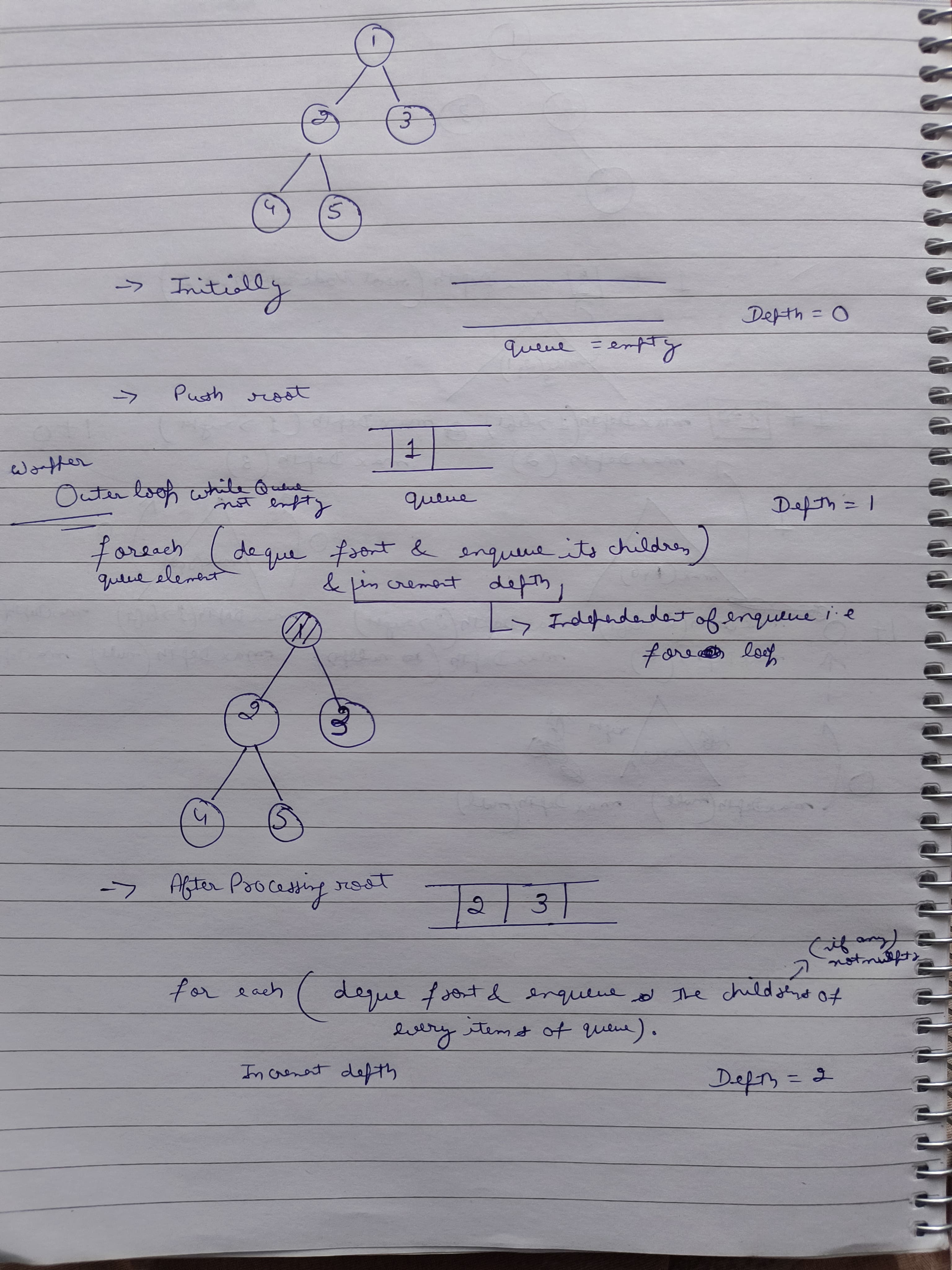
To determine the maximum depth of a binary tree using level order traversal, envision the process as a breadth-first exploration. Begin by initializing a queue and placing the root node into it. As each level of the tree is traversed, keep track of the depth by counting the number of levels visited. At each level, remove nodes from the queue and add their left and right children. Increment the depth counter as the level progresses. This exploration continues until there are no more levels to visit, at which point the depth counter will indicate the maximum depth of the tree.

We can also use iterative techniques such as level-order traversal (Breadth-First Search) to find the maximum depth of the binary tree.

Function maxDepth(root):
    If root is null:
        Return 0
    
    Initialize a queue
    Enqueue root into the queue
    Initialize depth to 0
    
    While the queue is not empty:
        Increment depth by 1
        Get the size of the queue (to process one level at a time)
        
        Loop over the nodes in the current level:
            Dequeue a node from the queue
            If the dequeued node has a left child, enqueue it
            If the dequeued node has a right child, enqueue it
            
    Return depth

Approach:

1. Begin by setting up a queue for level order traversal and a variable called depth to keep track of the tree's depth. If the root is null, return 0, indicating that the tree is empty. Otherwise, add the root node to the queue and initialize depth to 0.
2. Continue processing as long as the queue is not empty: Increment depth by 1 to advance to the next level. For each node at the current level (based on the number of elements in the queue), remove the node from the front of the queue and enqueue its left and right children if they are present.
3. Once the loop completes, return depth, which indicates the maximum depth of the tree.

Explanation:

1. Base Case: If the root node is null, the tree is empty, and its depth is 0. We return 0.
2. Initialization: We initialize a queue to perform level-order traversal. We enqueue the root node and initialize the depth of the tree to 0.
3. Level-Order Traversal: We perform a loop until the queue is empty, representing each level of the tree. In each iteration:
   1. We increment the depth by 1 to indicate that we are moving to the next level.
   2. We get the size of the queue, representing the number of nodes at the current level.
   3. We loop over each node in the current level:
      1. Dequeue a node from the queue.
      2. If the dequeued node has a left child, we enqueue it.
      3. If the dequeued node has a right child, we enqueue it.
4. Return Depth: After traversing all levels of the tree, we return the final depth, representing the maximum depth of the binary tree.

Code:

#include <iostream>
#include <queue>

struct TreeNode {
    int val;
    TreeNode* left;
    TreeNode* right;
    TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
};

int maxDepthIterative(TreeNode* root) {
    // If the root is null, the tree is empty, so the depth is 0
    if (root == nullptr)
        return 0;

    // Initialize a queue for level-order traversal and enqueue the root node
    std::queue<TreeNode*> q;
    q.push(root);

    // Initialize depth to 0
    int depth = 0;

    // Loop until all levels of the tree have been traversed
    while (!q.empty()) {
        // Get the number of nodes at the current level
        int levelSize = q.size();

        // Process all nodes at the current level
        for (int i = 0; i < levelSize; ++i) {
            // Dequeue the current node
            TreeNode* node = q.front();
            q.pop();

            // Enqueue the left child if it exists
            if (node->left)
                q.push(node->left);

            // Enqueue the right child if it exists
            if (node->right)
                q.push(node->right);
        }

        // Increment depth after processing all nodes at the current level
        depth++;
    }

    // Return the final depth after traversing all levels
    return depth;
}

int main() {
    // Example binary tree creation
    TreeNode* root = new TreeNode(1);
    root->left = new TreeNode(2);
    root->right = new TreeNode(3);
    root->right->left = new TreeNode(4);
    root->right->right = new TreeNode(5);

    // Call the iterative function to find the maximum depth
    std::cout << "Maximum Depth of the Binary Tree (Iterative Approach): " << maxDepthIterative(root) << std::endl;

    return 0;
}

Explanation:

1. We start by checking if the root is null. If it is, the tree is empty, so the depth is 0.
2. We initialize a queue for level-order traversal and enqueue the root node.
3. We initialize the depth counter to 0 to keep track of the current depth.
4. We enter a while loop that continues until all levels of the tree have been traversed (i.e., the queue becomes empty).
5. Inside the loop, we get the number of nodes at the current level by getting the size of the queue.
6. We iterate through all nodes at the current level using a for loop.
7. For each node, we dequeue it from the queue and enqueue its children (if they exist).
8. After processing all nodes at the current level, we increment the depth counter to move to the next level.
9. Finally, we return the depth after traversing all levels of the tree.

Complexity Analysis:

• Time Complexity: O(N)
  • The iterative approach, using level-order traversal, visits each node exactly once, resulting in a time complexity of O(N), where N is the number of nodes in the tree.
• Space Complexity: O(w), where w is the maximum width of the tree.
  • The space complexity of the iterative approach depends on the maximum number of nodes at any level of the binary tree, which corresponds to the maximum number of nodes in a level. In the worst-case scenario, the maximum number of nodes at any level is (N/2), where N is the number of nodes in the last level.
  • Therefore, the space complexity of the iterative approach is O(N) in the worst-case scenario.
  • In the average case or when the tree is balanced, the space complexity is typically less than O(N), but it can still be considered O(N) due to the need for storing nodes at each level.