Problem Statement

Given an array arr of size n containing elements, find the next greater element for each element in the array in the order of their appearance.

The next greater element of an element in the array is the nearest element on the right that is greater than the current element.

If there does not exist a next greater element for the current element, then the next greater element for that element is -1.

Examples

Example 1:

Input: arr = [1, 3, 2, 4]
Output: [3, 4, 4, -1]

Explanation: In the array, the next larger element to 1 is 3, 3 is 4, 2 is 4, and for 4 is -1, since it does not exist.

Example 2:

Input: arr = [6, 8, 0, 1, 3]
Output: [8, -1, 1, 3, -1]

Explanation: In the array, the next larger element to 6 is 8, for 8 there is no larger elements hence it is -1, for 0 it is 1, for 1 it is 3 and then for 3 there is no larger element on the right and hence -1.

Different Approaches

1️⃣ Brute Force Approach

Intuition:

A naive approach to solve this question will be to use a loop to pick up an element of the array, and then find its next greater element using a nested loop. In case there is no larger element found on the right of the current element, the next greater element will be set to -1.

Approach:

1. Initialize an array answer to store the next greater elements for the given array with all elements initially set to -1.
2. Traverse the array using a for loop to select the current element for which the next greater element must be found.
3. Use a nested for loop to traverse the right side of the array (from the current element) to find the next greater element. If found, store the answer in the answer array and break from the inner loop.
4. Once the outer for loop ends, the answer array storing the result can be returned.

Dry Run:

      +-----+-----+-----+-----+
arr = |  1  |  3  |  2  |  4  |
      +-----+-----+-----+-----+
         0     1     2     3

      +-----+-----+-----+-----+
ans = | -1  | -1  | -1  | -1  |
      +-----+-----+-----+-----+
         0     1     2     3

Iteration i = 0, j = 1:

      +-----+-----+-----+-----+
arr = |  1  |  3  |  2  |  4  |
      +-----+-----+-----+-----+
         0     1     2     3
         ^     ^
         |     |
         i     j

      +-----+-----+-----+-----+
ans = | -1  | -1  | -1  | -1  |
      +-----+-----+-----+-----+
         0     1     2     3

Code:

#include <bits/stdc++.h>
using namespace std;

class Solution {
public:

    /* Function to find the next greater 
    element for each element in the array */
    vector<int> nextLargerElement(vector<int> arr) {
        
        int n = arr.size(); // size of array
        
        // To store the next greater elements
        vector<int> ans(n, -1);
        
        for(int i=0; i < n; i++) {
            
            // Get the current element+
            int currEle = arr[i];
            
            /* Nested loop to get the 
            next greater element */
            for(int j=i+1; j < n; j++) {
                
                // If the next greater element is found
                if(arr[j] > currEle) {
                    
                    // Store the next greater element
                    ans[i] = arr[j];
                    
                    // Break from the loop
                    break;
                }    
            }
        }
        
        // Return the answer
        return ans;
    }
};

int main() {
    int n = 4;
    vector<int> arr = {1, 3, 2, 4};

    /* Creating an instance of 
    Solution class */
    Solution sol; 
    
    /* Function call to find the next greater element
    for each element in the circular array */
    vector<int> ans = sol.nextLargerElement(arr);
    
    cout << "The next greater elements are: ";
    for(int i=0; i < n; i++) {
        cout << ans[i] << " ";
    }
    
    return 0;
}

Complexity Analysis:

• Time Complexity: O(N^2) (where N is the size of given array)
  • Using two nested for loops to find the next greater elements.
• Space Complexity: O(N) The space required to store the answer is O(N).

2️⃣ Optimal Approach

Intuition:

In order to obtain the next greater element (which will always be on the right side) for a particular element, if we traverse the array from the beginning to the end, it is impossible to know the right elements beforehand as they will be unvisited. But if the traversal is done from the end to the beginning of array, it will be easier to find the next greater element cause all the right elements will be already visited(known) to us. Thus, we will start the traversal from back and the whole discussion will be based on the same.

Now since, we are traversing from the back, the question is now to find the last greatest element. Hence, no matter how many greater elements we encounter, the only greater element we must consider first is the last greater element that was seen. This gives an idea of using stack data structure because it stores elements in the Last In First Out fashion. Now, comes the question of how to store the elements in the stack?

Understanding:

Since, we are considered about the greater elements only, it makes sense to store(push) the elements in the stack in a decreasing order (smaller elements are on the top and larger elements on the bottom). So that for every element that we found, the stack already contains greater elements (potentially).

But it is not always guaranteed that the top of the stack will be greater than the current element (for which the next greater element is to be found). In such scenarios, we can pop elements from the stack till we get a greater element. If a greater element is found, it can be stored as the answer otherwise -1 can be stored as answer. Once the answer is stored, the current element can be stored in the stack maintaining the decreasing order of elements.

Approach:

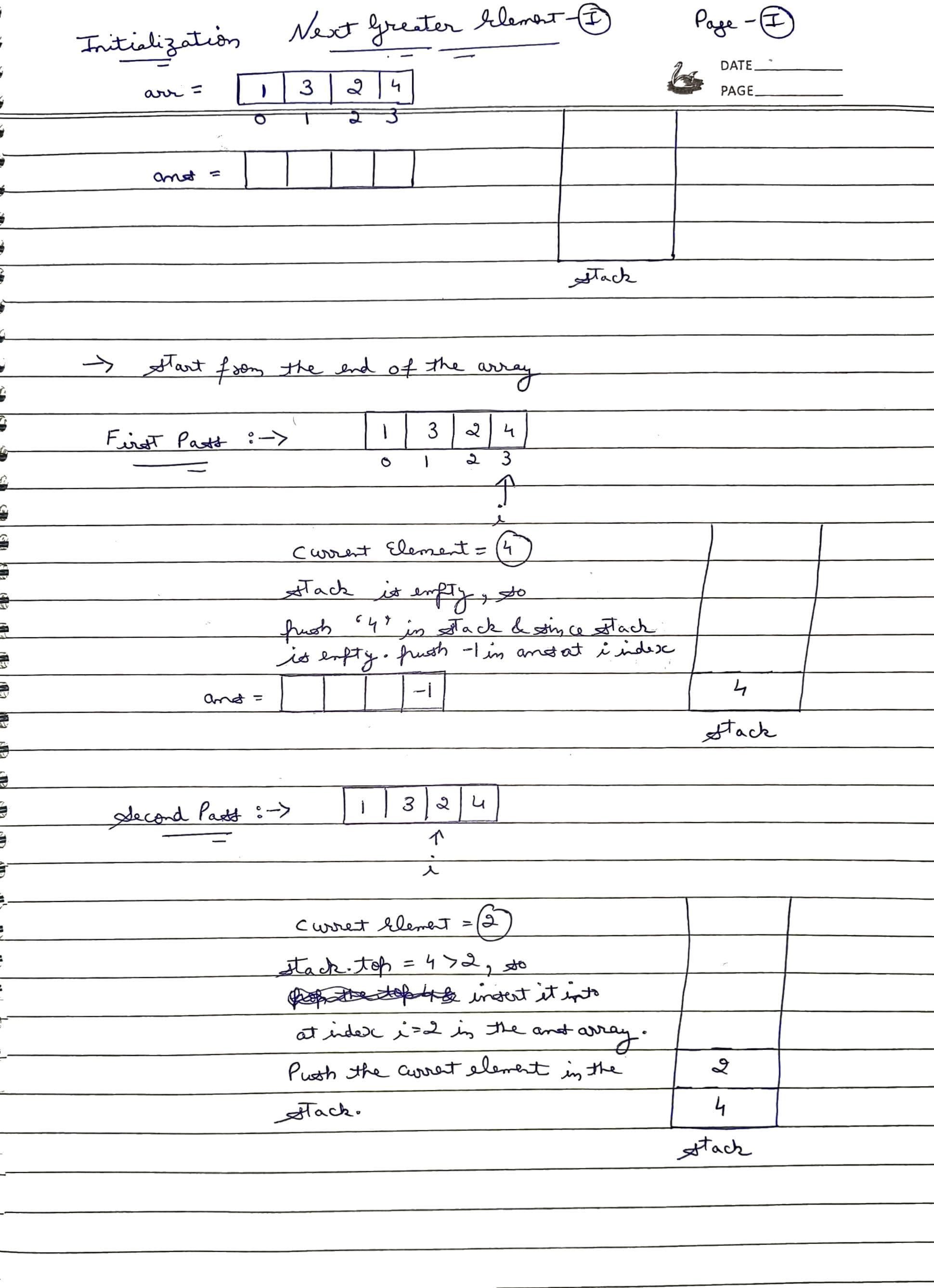
1. Initialize an answer array to store the next greater elements for the given array. Declare a stack data structure.
2. Start traversing the array from back. For current element, pop the elements from stack till the top is less than or equal to the current element.
3. If a greater element is found, store it in the answer array, otherwise store -1. Push the current element in the stack maintaining decreasing order.
4. Once the traversal on array is complete, the answer array stores the result.

Dry Run:

Code:

#include <bits/stdc++.h>
using namespace std;

class Solution {
public:

    /* Function to find the next greater 
    element for each element in the array */
    vector<int> nextLargerElement(vector<int> arr) {
        
        int n = arr.size(); //size of array
        
        // To store the next greater elements
        vector<int> ans(n);
        
        // Stack to get elements in LIFO fashion
        stack<int> st;
        
        // Start traversing from the back
        for(int i=n-1; i >= 0; i--) {
            
            // Get the current element
            int currEle = arr[i];
            
            /* Pop the elements in the stack until 
            the stack is not empty and the top 
            element is not the greater element */
            while(!st.empty() && st.top() <= currEle) {
                st.pop();
            }
            
            /* If the greater element is not 
            found, stack will be empty */
            if(st.empty()) 
                ans[i] = -1;
                
            // Else store the answer
            else 
                ans[i] = st.top();
            
            /* Push the current element in the stack 
            maintaining the decreasing order */
            st.push(currEle);
        }
        
        // Return the result
        return ans;
    }
};

int main() {
    int n = 4;
    vector<int> arr = {1, 3, 2, 4};
    
    /* Creating an instance of 
    Solution class */
    Solution sol; 
    
    /* Function call to find the next greater 
    element for each element in the array */
    vector<int> ans = sol.nextLargerElement(arr);
    
    cout << "The next greater elements are: ";
    for(int i=0; i < n; i++) {
        cout << ans[i] << " ";
    }
    
    return 0;
}

Complexity Analysis:

• Time Complexity: O(N) (where N is the size of the array)
  • Traversing on the hypothetical array takes O(2N) time and traversing the stack will take overall O(2N) time as all the elements are pushed in the stack once.
• Space Complexity: O(N)
  • The answer array takes O(N) space and the space used by stack will be O(N) in the worst case.