Problem Statement
Given an array arr where arr[i] represents the price of a given stock on the ith day. Additionally, you are given an integer fee representing a transaction fee for each trade. The task is to determine the maximum profit you can achieve such that you need to pay a transaction fee for each buy and sell transaction. The Transaction Fee is applied when you sell a stock.
You may complete as many transactions. You may not engage in multiple transactions simultaneously (i.e., you must sell the stock before buying again).
Examples
Example 1:
Input: arr = [1, 3, 4, 0, 2], fee = 1
Output: 3
Explanation:
Buy at day 1, sell at day 3, then, buy at day 4, sell at day 5.
Profit calculation: ((4 - 1) - 1) + ((2 - 0) - 1) = 2 + 1 = 3.Example 2:
Input: arr = [1, 3, 2, 8, 4, 9], fee = 2
Output: 8
Explanation:
Buy at day 1 (price = 1), sell at day 4 (price = 8), then Buy at day 5 (price = 4), sell at day 6 (price = 9),
Profit calculation: ((9 - 4) - 2) + ((8 - 1) - 2)= 8.Different Approaches
1️⃣ Recursive Approach
Upon observation, we find that every day, there will be two choices, either to do nothing and move to the next day or to buy/sell (based on the last transaction and the number of transactions left) and find out the profit. Therefore we need to generate all the choices in order to compare the profit. As all possible choices needs to be generated, we will use recursion.
Steps to form the recursive solution:
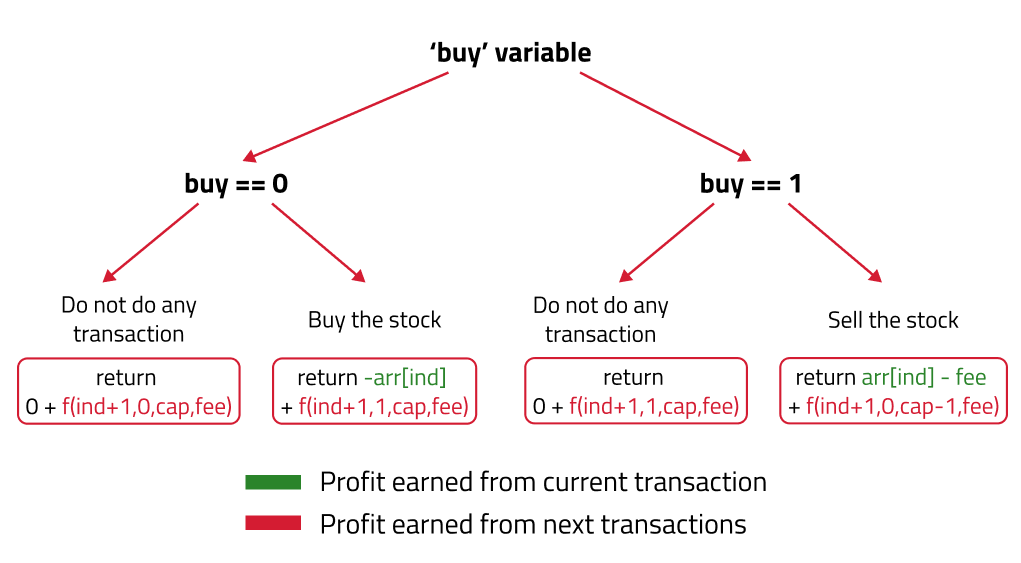
- Express the problem in terms of indexes: We need to think in the terms of the number of days, therefore one variable will be the array index( say ind). Next, we need to consider the condition that a stock can't be bought again, that is we need to first sell a stock, and then we can buy that again. Therefore a second variable ‘buy’ is needed, which tells, on a particular day whether we can buy or sell the stock. Next, there is a fee applied on every complete transaction. So in order to keep track of this, one more variable will be needed (say 'fee').
- f(ind, buy, fee) will give the maximum profit that can be generated from day 'ind' to day (n-1), where 'buy' tells that whether we need to buy or sell the stock at day 'ind' and 'fee' tells the fee incurred at every complete transaction.
- Try out all possible choices at a given index: Every day, there will be two choices, either to buy/sell the stock(based on the buy variable’s value) or to do nothing and move on to the next day. As we need to generate all the choices, use the pick/non-pick technique to the same.
- Case 1: When buy == 0, the stock can be bought. If we can buy the stock on a particular day, there will be two options:
- Option 1: To do no transaction and move to the next day. In this case, the net profit earned will be 0 from the current transaction, and to calculate the maximum profit starting from the next day, we will recursively call f(ind+1, 0, fee). As we have not bought the stock, the ‘buy’ variable value will still remain 0, indicating that stock can be bought on next day.
- Option 2: The other option is to buy the stock on the current day. In this case, the net profit earned from the current transaction will be -Arr[i]. As we are buying the stock, we are giving money out of our pocket, therefore the profit we earn is negative. To calculate the maximum profit starting from the next day, recursively call f(ind+1,1, fee). As the stock has been bought, the ‘buy’ variable value will change to 1, indicating that we can’t buy and only sell the stock the next day.
- Case 2: When buy == 1, we can sell the stock. If we can sell the stock on a particular day, we will have two options:
- Option 1: To do no transaction and move to the next day. In this case, the net profit earned will be 0 from the current transaction, and to calculate the maximum profit starting from the next day, we will recursively call f(ind+1,1, fee). As we have not bought the stock, the ‘buy’ variable value will still remain at 1, indicating that we can’t buy and only sell the stock the next day.
- Option 2: The other option is to sell the stock on the current day. In this case, the net profit earned from the current transaction will be +Arr[i]. As we are selling the stock, we are putting the money into our pocket, therefore the profit we earn is positive. Next, as we have bought and sold the stock, one complete transaction has been made. Hence the transaction fees will be incurred. So subtract that from the profit earned. To calculate the maximum profit starting from the next day, we will recursively call f(ind+1, 0, fee). As we have sold the stock, the ‘buy’ variable value will change to 0, indicating that we can buy the stock the next day.
- Case 1: When buy == 0, the stock can be bought. If we can buy the stock on a particular day, there will be two options:
Note: Buying and selling a stock together counts as one complete transaction. Therefore the fee will be deducted once after selling every stock.
/*It is pseudocode and it is not tied to
any specific programming language*/
f(ind, buy, fee){
//Base case woulbe be here
if(buy == 0){
// we can buy
// Do nothing, and proceed to the next index
// price for buying.
op1 = 0 + f(ind + 1, 0, fee)
// Buy at current price and proceed to the next
// index price for selling.
op2 = -arr[ind] + f(ind + 1, 1, fee)
}
if(buy == 1){
// We already bought, here to sell.
//
Do nothing, and proceed to the next index
// price for selling
op1 = 0 + f(ind + 1, 1, fee)
// Sell at current price and proceed to the
// next index price for buying again.
op2 = arr[ind] - fee + f(ind + 1, 0, fee)
}
}- Take the maximum of all choices: As we are looking to maximize the profit earned, return the maximum value in both cases.
/*It is pseudocode and it is not tied to
any specific programming language*/
f(ind, buy, fee){
//Base case woulbe be here
if(buy == 0){
// we can buy
// Do nothing, and proceed to the next index
// price for buying.
op1 = 0 + f(ind + 1, 0, fee)
// Buy at current price and proceed to the next
// index price for selling.
op2 = -arr[ind] + f(ind + 1, 1, fee)
}
if(buy == 1){
// We already bought, here to sell.
//
Do nothing, and proceed to the next index
// price for selling
op1 = 0 + f(ind + 1, 1, fee)
// Sell at current price and proceed to the
// next index price for buying again.
op2 = arr[ind] - fee + f(ind + 1, 0, fee)
}
return max(op1, op2);
}- Base cases:
- There be will only one base case, when ind==n, it means we have finished trading on all days, and no more profit can be made, therefore simply return 0.
Code:
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
class Solution {
public:
// Recursive function to calculate max profit
int maxProfit(int day, bool canBuy, vector<int>& prices, int fee) {
// Base case: If all days are processed
if (day == prices.size()) return 0;
// If we can buy (canBuy == true)
if (canBuy) {
// Either skip the day or buy the stock
return max(maxProfit(day + 1, true, prices, fee), // Skip buying
-prices[day] + maxProfit(day + 1, false, prices, fee)); // Buy stock
}
// If we cannot buy (canBuy == false), we can sell the stock
else {
// Either skip the day or sell the stock and pay the fee
return max(maxProfit(day + 1, false, prices, fee), // Skip selling
prices[day] - fee + maxProfit(day + 1, true, prices, fee)); // Sell stock
}
}
// Public function to start the recursive calls
int maxProfit(vector<int>& prices, int fee) {
return maxProfit(0, true, prices, fee); // Start from day 0, with the option to buy
}
};
int main() {
vector<int> prices = {1, 3, 2, 8, 4, 9}; // Stock prices
int fee = 2; // Transaction fee
// Create an instance of Solution class
Solution solution;
// Call the maxProfit function and print the result
cout << "The maximum profit with transaction fee is "
<< solution.maxProfit(prices, fee) << endl;
return 0;
}
Complexity Analysis:
- Time Complexity:
O(2^(N)), whereNis the number of row. As, for each index, ther are two possible options. - Space Complexity:
O(N), at maximum the depth of the recursive stack can go up-toN.
