Understanding the Problem

Tree traversal involves visiting and processing each node in a tree data structure. Pre-order traversal specially follows the order: Root, Left, Right. This means that you visit the root node first, then recursively traverse the left subtree, and finally, traverse the right subtree.

Consider the following binary tree:

        1
       / \
      2   3
     / \
    4   5

The pre-order traversal of this tree would be 1, 2, 4, 5, 3.

Different Approaches

1️⃣ Recursive Approach

Intuition:

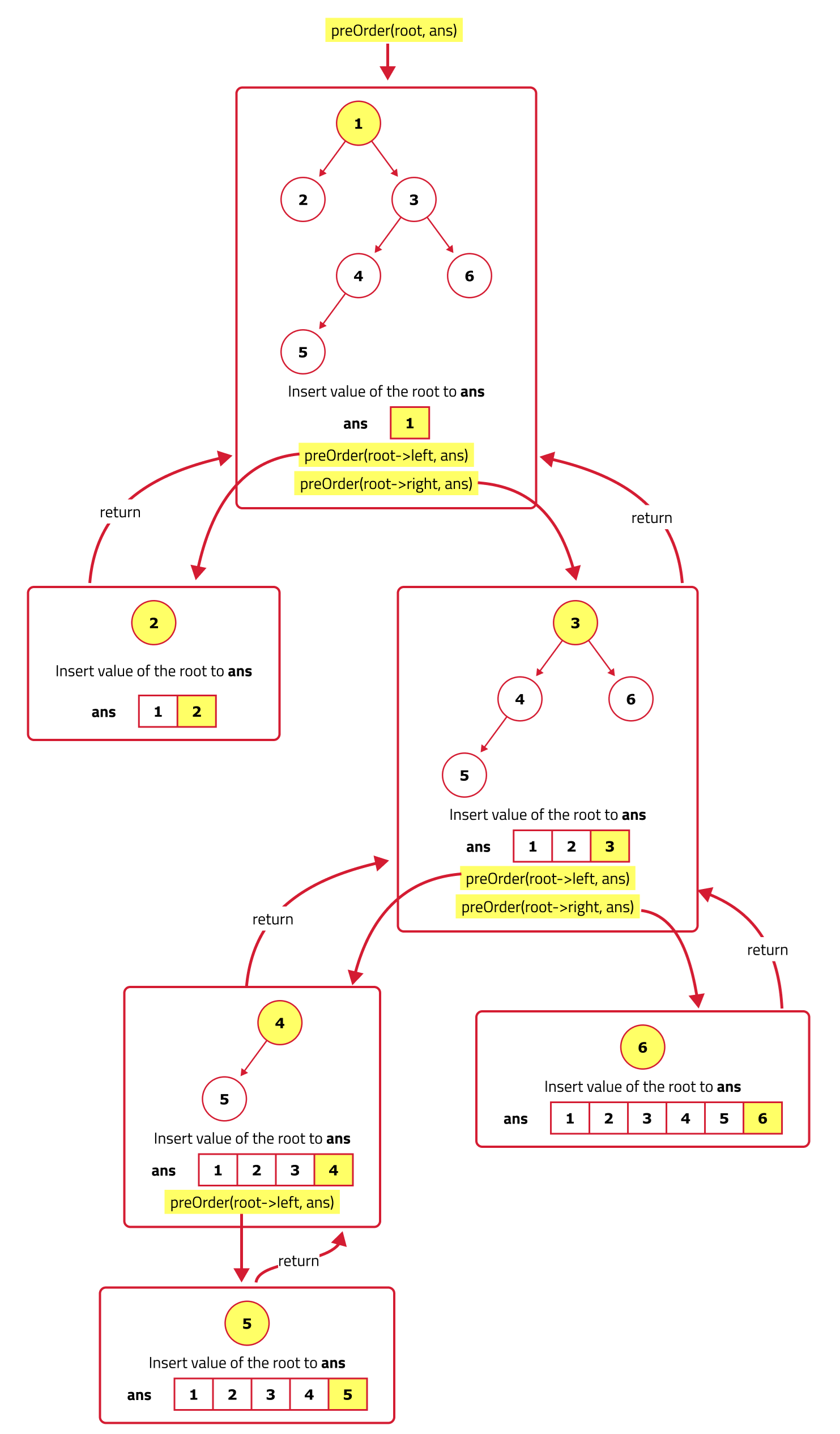
Preorder traversal is one of the depth-first traversal methods used to explore nodes in a binary tree. The algorithm first visits the root node, then in the preorder traversal, we visit (i.e., add to the array) the current node by accessing its value, then we recursively traverse the left subtree in the same manner. We repeat these steps for the left subtree, then when we return to the current node, we recursively travel to the right subtree in a preorder manner as well. The sequence of steps in preorder traversal follows: Root, Left, Right.

The recursive approach is the most straightforward method for pre-order traversal. The algorithm follows these steps:

1. Visit the root node.
2. Recursively perform a pre-order traversal on the left subtree.
3. Recursively perform a pre-order traversal on the right subtree.

Approach:

1. Base Case: If the current node is null, it means we have reached the end of a subtree and there are no further nodes to explore. Hence the recursive function stops and we return from that particular recursive call.
2. Recursive Function:
   1. Process Current Node: The recursive function begins by processing i.e., adding to the array or printing the current node.
   2. Traverse Left Subtree: Recursively traverse the left subtree by invoking the preorder function on the left child of the current node. This step continues the exploration of nodes in a depth-first manner.
   3. Traverse Right Subtree: After traversing the entire left subtree, we traverse the right subtree recursively. We once again invoke the preorder function, but this time on the right child of the current node.

Dry Run:

Code:

#include <bits/stdc++.h>
using namespace std;

// Definition for a binary tree node
struct TreeNode {
    int data;
    TreeNode* left;
    TreeNode* right;

    // Constructor to initialize a node with a value
    TreeNode(int val) : data(val), left(nullptr), right(nullptr) {}
};

class Solution {
public:
    // Helper function to perform preorder traversal
    void func(TreeNode* node, vector<int>& ans) {
        // If the current node is null, return (base case for recursion)
        if (node == nullptr) {
            return;
        }

        // Append the current node's value to the list
        ans.push_back(node->data);
        // Recursively traverse the left subtree
        func(node->left, ans);
        // Recursively traverse the right subtree
        func(node->right, ans);
    }

    // Function to initiate preorder traversal and return the resulting vector
    vector<int> preorder(TreeNode* root) {
        // Create an empty vector to store preorder traversal values
        vector<int> ans;
        // Call the helper function with the root node and the vector
        func(root, ans);
        // Return the resulting vector containing preorder traversal values
        return ans;
    }
};

// Main function to test the preorder traversal
int main() {
    // Creating a sample binary tree
    TreeNode* root = new TreeNode(1);
    root->left = new TreeNode(2);
    root->right = new TreeNode(3);
    root->left->left = new TreeNode(4);
    root->left->right = new TreeNode(5);

    // Create an instance of the Solution class
    Solution solution;
    // Getting preorder traversal
    vector<int> result = solution.preorder(root);

    // Displaying the preorder traversal result
    cout << "Preorder Traversal: ";
    for (int val : result) {
        cout << val << " ";
    }
    cout << endl;

    return 0;
}

Complexity Analysis

• Time Complexity: O(N) - where N is the number of nodes in the tree.
  • As each node of the binary tree is visited exactly once.
• Space Complexity: O(N), where N is the number of nodes in the binary tree, as an additional space for the array is allocated to store the values of all N nodes of the binary tree.

2️⃣ Iterative Approach using Stack:

An iterative approach using a stack can also be employed for pre-order traversal. The algorithm involves pushing nodes onto the stack. If the left subtree is exhausted, the algorithm pops node from the stack and traverse their right subtrees.

Approach:

1. Initially, the root node is pushed into the stack. While the stack is not empty, we continuously pop nodes from the stack and for each popped node, we add its value to the resultant traversal vector, push its right child onto the stack followed by its left child.
2. This sequence ensures that the left child, which should be processed first in the preorder traversal, is visited before the right child due to the Last In, First Out behavior of the stack. This process continues until all nodes are processed.

Dry Run:

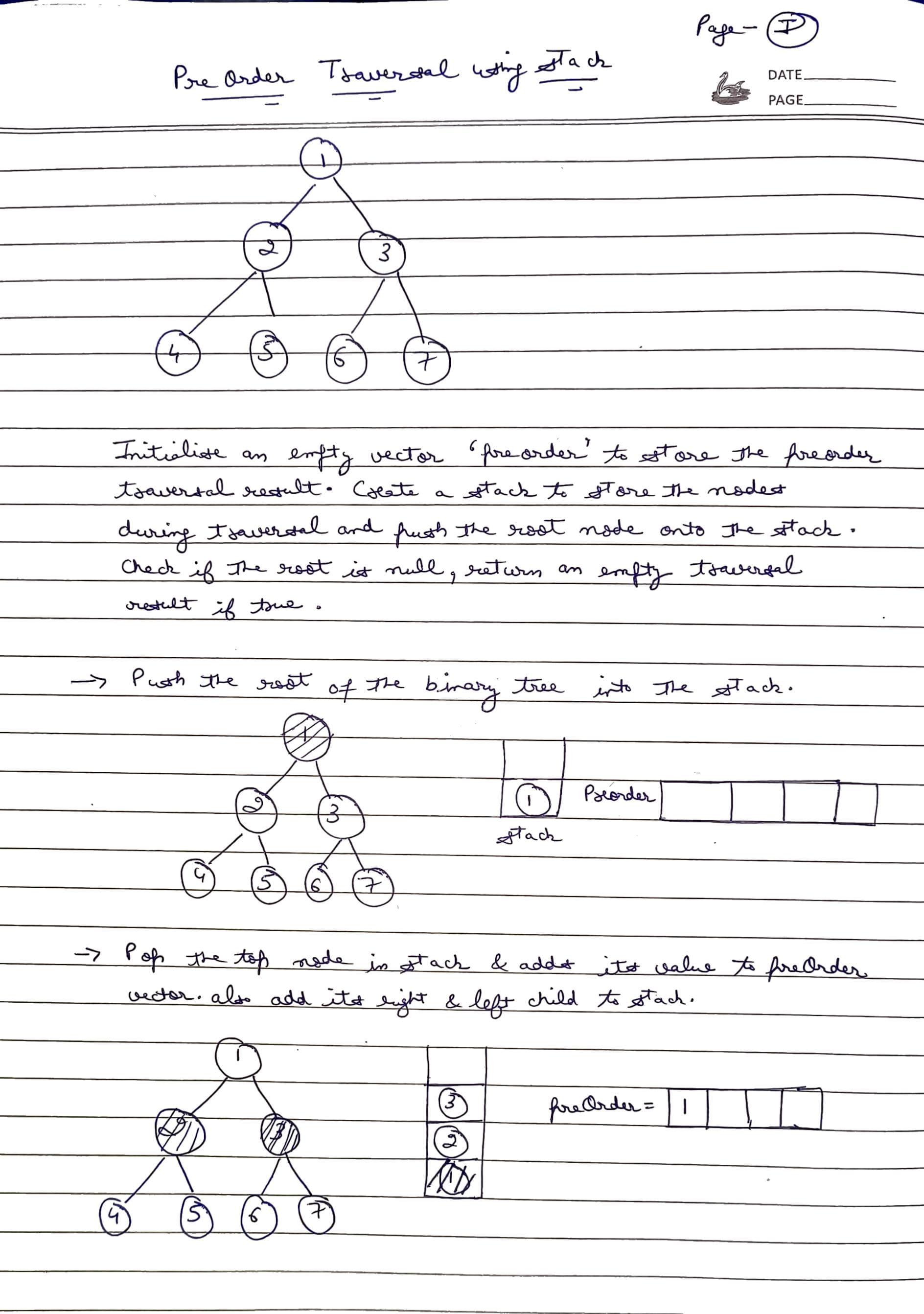
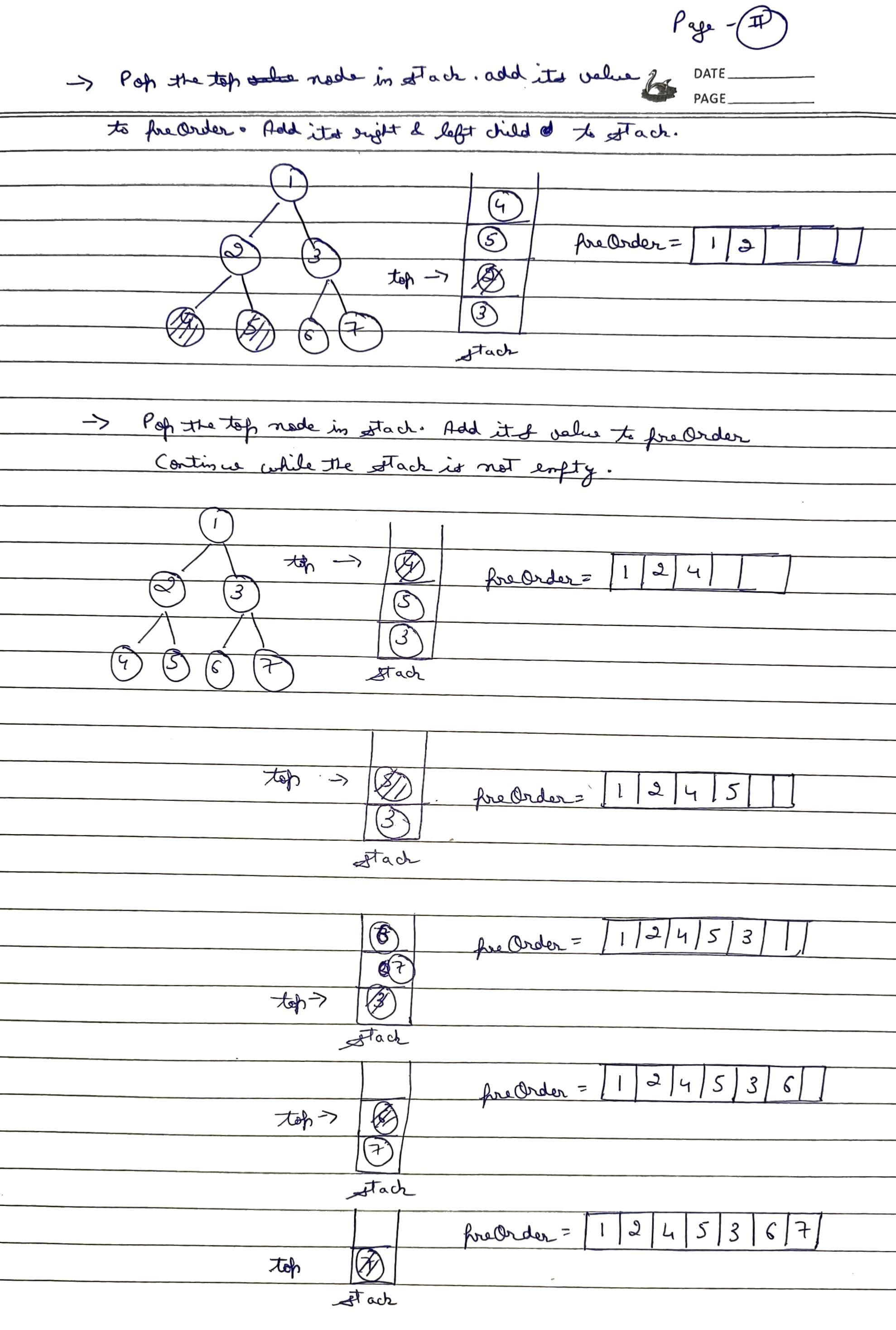
Code:

#include <iostrean>
#include <vector>
#include <stack>

using namespace std;

// Define the TreeNode structure
struct TreeNode {
    int data;
    TreeNode* left;
    TreeNode* right;
    TreeNode(int x) : data(x), left(nullptr), right(nullptr) {}
};

class Solution {
public:
    // Function to perform preorder traversal
    // of a binary tree iteratively
    vector<int> preorder(TreeNode* root) {
        // Initialize vector to store
        // the preorder traversal result
        vector<int> preorder;
        
        // If the root is null, return
        // an empty traversal result
        if(root == nullptr) {
            return preorder;
        }
        
        // Create a stack to store
        // nodes during traversal
        stack<TreeNode*> st;
        // Push the root node
        // onto the stack
        st.push(root);
        
        // Perform iterative preorder traversal
        while(!st.empty()) {
            // Get the current node
            // from the top of the stack
            root = st.top();
            // Remove the node
            // from the stack
            st.pop();
            
            // Add the node's value to
            // the preorder traversal result
            preorder.push_back(root->data);
            
            // Push the right child
            // onto the stack if exists
            if(root->right != nullptr) {
                st.push(root->right);
            }
            
            // Push the left child onto
            // the stack if exists
            if(root->left != nullptr) {
                st.push(root->left);
            }
        }
        
        // Return the preorder
        // traversal result
        return preorder;
    }
};

int main() {
    // Creating a binary tree
    TreeNode* root = new TreeNode(1);
    root->left = new TreeNode(2);
    root->right = new TreeNode(3);
    root->left->left = new TreeNode(4);
    root->left->right = new TreeNode(5);

    // Initializing the Solution class
    Solution sol;

    // Getting the preorder traversal
    vector<int> result = sol.preorder(root);

    // Displaying the preorder traversal result
    cout << "Preorder Traversal: ";
    for (int val : result) {
        cout << val << " ";
    }
    cout << endl;

    return 0;
}

Complexity Analysis:

• Time Complexity: O(N) where N is the number of nodes in the binary tree. Every node of the binary tree is visited exactly once, and for each node, the operations performed (pushing and popping from the stack, accessing node values, etc.) are constant time operations.
• Space Complexity: O(N) where N is the number of nodes in the binary tree. This is because the stack can potentially hold all nodes in the tree when dealing with a skewed tree (all nodes have only one child), consuming space proportional to the number of nodes. In the average case or for a balanced tree, the maximum number of nodes that could be in the stack at any given time would be roughly the height of the tree, hence O(log2N).

In both cases, the space complexity is determined by the height of the tree. For a balanced tree, the height is logarithmic in the number of nodes, making the space complexity O(log N). However, for a skewed tree, the height is equal to the number of nodes, resulting in a space complexity of O(N).