Problem Statement

A frog wants to climb a staircase with n steps. Given an integer array heights, where heights[i] contains the height of the ith step.

To jump from the ith step to the jth step, the frog requires abs(heights[i] - heights[j]) energy, where abs() denotes the absolute difference. The frog can jump from any step either one or two steps, provided it exists. Return the minimum amount of energy required by the frog to go from the 0th step to the (n-1)th step.

Given:

heights[]: an array where heights[i] represents the height of the i-th step.
The frog can either jump from step i to step i+1 or from step i to step i+2.
The energy cost for a jump from step i to step j is calculated as abs(heights[i] - heights[j]).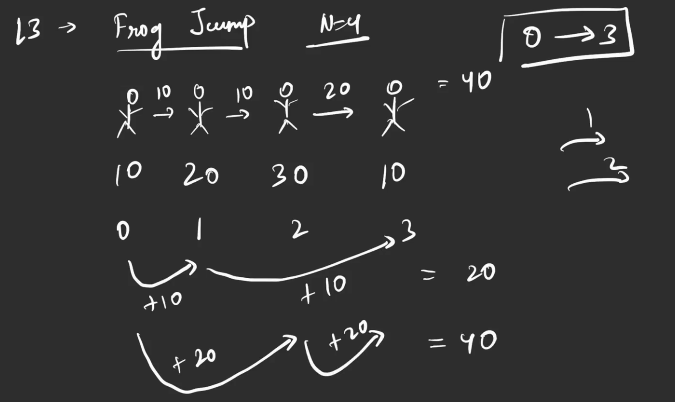

Examples

Example 1:

Input: heights = [2, 1, 3, 5, 4]
Output: 2

Explanation: One possible route can be,
0th step -> 2nd Step = abs(2 - 3) = 1
2nd step -> 4th step = abs(3 - 4) = 1
Total = 1 + 1 = 2.

Example 2:

Input: heights = [7, 5, 1, 2, 6]
Output: 9

Explanation: One possible route can be,
0th step -> 1st Step = abs(7 - 5) = 2
1st step -> 3rd step = abs(5 - 2) = 3
3rd step -> 4th step = abs(2 - 6) = 4
Total = 2 + 3 + 4 = 9.

Different Approach

1️⃣ Recursion

Why Greedy Doesn't Work:

In the greedy approach, the frog makes a locally optimal choice at each step, always jumping to the stone with the least immediate cost. However, this can lead to suboptimal solutions because a sequence of cheaper initial jumps may trap the frog into making costly jumps later. The problem is that the greedy algorithm doesn't account for the future consequences of the current choices, so it doesn't guarantee the minimum overall cost.

For example:

• If the cost of jumping to the next stone is lower than jumping two stones ahead, the frog might choose to jump to the next stone. But this local choice could lead to higher cumulative energy due to future high costs.

Thus, dynamic programming is needed to evaluate all possible paths and determine the overall minimum cost.

Greedy Approach:

            +-----+-----+-----+-----+-----+-----+
heights  =  | 30  | 10  | 60  | 10  | 60  | 50  |
            +-----+-----+-----+-----+-----+-----+
stairs|index   0     1     2     3     4     5
               |    ^ |         ^ |          ^
               |    | |         | |          |
                ----   ---------   ----------
                 20        0           40
                 
          => 20 + 0 + 40 = 60

Non-Greedy | Recursion Approach:

            +-----+-----+-----+-----+-----+-----+
heights  =  | 30  | 10  | 60  | 10  | 60  | 50  |
            +-----+-----+-----+-----+-----+-----+
stairs|index   0     1     2     3     4     5
               |          ^ |         ^ |    ^
               |          | |         | |    |
                ----------   ---------   ----
                    30           0         10
          
          => 30 + 0 + 10 = 40

Approach:

1. Define the problem in terms of indices. The array indexes [0, 1, 2, ..., n-1] represent the stairs. The function f(n-1) represents the minimum energy needed to jump from stair 0 to stair n-1. The base case is f(0) = 0.
2. Explore all possible choices to reach the target stair. The frog can jump either one step or two steps. The cost of each jump is derived from the height array, and the remaining cost is obtained through recursive calls.
3. Return the minimum energy from the possible choices in Step 2. Since the goal is to minimize the total energy, the function should return the lesser of the two computed energies. At index 1, only one recursive call is possible, as the second choice is not feasible. The base case for this scenario is reaching the 0th stair.

Code:

#include<bits/stdc++.h>
using namespace std;

class Solution {
public:
    int frogJump(vector<int>& heights, int ind) {
        // Base case: if the frog is at the first step
        if (ind == 0) return 0;
        
        // Recursively calculate the energy required to
       // jump to the current step from the previous step
        int jumpOne = frogJump(heights, ind - 1) + abs(heights[ind] - heights[ind - 1]);
        
        // Initialize jumpTwo to a large value
        int jumpTwo = INT_MAX;
        
        // If possible, recursively calculate the energy required to
       //  jump to the current step from two steps back
        if (ind > 1) {
            jumpTwo = frogJump(heights, ind - 2) + abs(heights[ind] - heights[ind - 2]);
        }
        
        // Return the minimum energy required to reach the current step
        return min(jumpOne, jumpTwo);
    }

    int frogJump(vector<int>& heights) {
        int n = heights.size();
        return frogJump(heights, n - 1);
    }
};

int main() {
    Solution sol;
    vector<int> heights = {2, 1, 3, 5, 4};
    int result = sol.frogJump(heights);
    cout << "Minimum energy required: " << result << endl;
    return 0;
}

Complexity Analysis:

• Time Complexity: O(N), where n is the number of stairs.
• Space Complexity: O(N) due to the recursion stack and the storage of intermediate results.

2️⃣ Memoization:

Intuition:

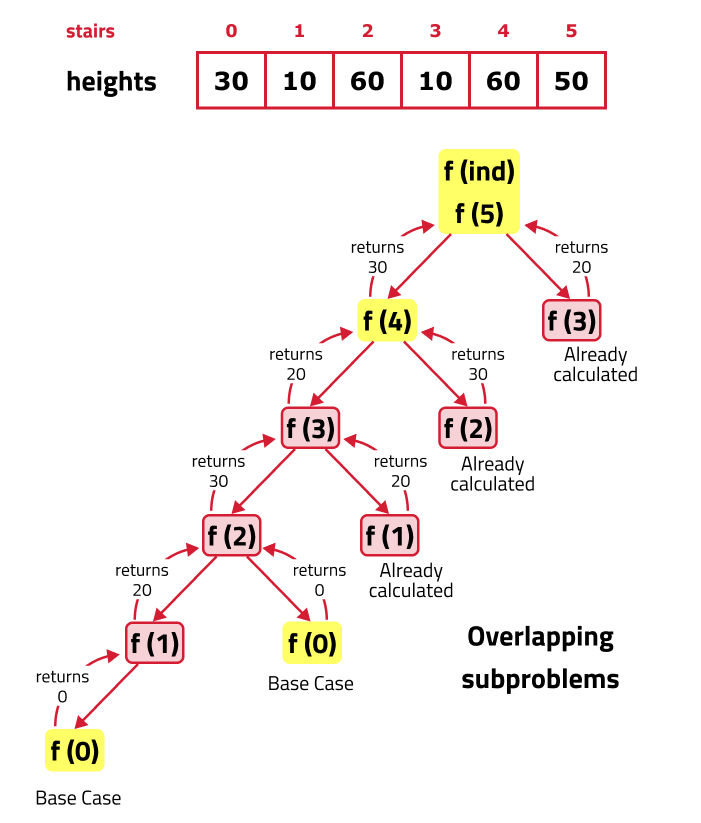
To optimize the recursive solution for finding the minimum energy required for a frog to jump between stairs, the memoization approach can be employed. This technique involves storing intermediate results to prevent redundant calculations and enhance efficiency. The thought process is as follows: First, initialize an array to store the results of previously computed steps. Before calculating the energy required for a specific stair, check if it has already been computed. If so, use the stored value, thereby saving time. If not, compute the value as usual and store it in the array before returning it. This approach ensures that each unique computation is performed only once, significantly reducing the overall time complexity.

Memoization Approach:

The steps to convert the recursive solution to a memoized one are as follows:

• Create an array dp[n] initialized to -1 to store intermediate results.
• Before calculating the result for a particular stair, check if it has already been computed by verifying if dp[n] is not -1. If it has been computed, return the stored value.
• If the result has not been computed, calculate it using the recursive relation. Before returning the result, store it in the dp array to avoid redundant calculations in the future.

Recursion Tree:

Code:

#include<bits/stdc++.h>
using namespace std;

class Solution {
public:
    int solve(int ind, vector<int>& heights, vector<int>& dp) {
        // Base case
        if (ind == 0) return 0; 
        // Memoized result
        if (dp[ind] != -1) return dp[ind]; 

        int jumpOne = solve(ind - 1, heights, dp) + abs(heights[ind] - heights[ind - 1]);
        int jumpTwo = INT_MAX;
        if (ind > 1)
            jumpTwo = solve(ind - 2, heights, dp) + abs(heights[ind] - heights[ind - 2]);
        // Store and return result
        return dp[ind] = min(jumpOne, jumpTwo); 
    }

    int frogJump(vector<int>& heights) {
        int n = heights.size();
        vector<int> dp(n, -1);
        // Start solving from the last stair
        return solve(n - 1, heights, dp); 
    }
};

int main() {
    vector<int> heights = {30, 10, 60, 10, 60, 50};
    Solution sol;
    // Output the result
    cout << sol.frogJump(heights) << endl; 
    return 0;
}

Complexity Analysis:

• Time Complexity: O(n) due to the recursion with memoization and the linear loop for initialization.
  • Initialization of dp takes n time as it initializes all n elements to -1.
  • The recursion makes at most two calls, but memoization ensures no redundant computation so, there are total n recursive calls, which takes O(n).
  • Overall Time Complexity: O(n) + O(n) = O(n)
• Space Complexity:O(n) for the memoization array used to store intermediate results.
  • The dp vector stores n values, initialized to -1, so it has space complexity of O(n)
  • In the worst-case scenario, the recursion depth is n, thus O(n) for the recursion stack.
  • Overall Space Complexity: O(n) + O(n) = O(n)

3️⃣ Tabulation

Intuition:

To determine the minimum energy required for a frog to jump from the first to the last stair using the tabulation approach, the process involves constructing a table (or array) to store the minimum energy needed to reach each stair. This dynamic programming technique iteratively fills the table based on previously computed values, ensuring that each step is optimally calculated.

The tabulation approach begins by defining an array, dp, where each element represents the minimum energy required to reach the corresponding stair. By iterating through the array and calculating the energy for each jump, the solution can be efficiently derived.

Approach:

• Step 1: Declare a dp array of size n, where n is the number of stairs.
• Step 2: Initialize the base condition: dp[0] = 0, since no energy is required to stay on the first stair.
• Step 3: Set up an iterative loop to traverse the array from index 1 to n-1:
  • For each index i, calculate the energy required for a one-step jump (jumpOne) and a two-step jump (jumpTwo).
  • Update dp[i] with the minimum energy of the two possible jumps: dp[i] = min(jumpOne, jumpTwo).

Code:

#include<bits/stdc++.h>
using namespace std;

class Solution {
public:
    int frogJump(vector<int>& heights) {
        int n = heights.size();
        vector<int> dp(n, -1);
        dp[0] = 0; // Base case

        // Iterative calculation
        for (int ind = 1; ind < n; ind++) {
            int jumpOne = dp[ind - 1] + abs(heights[ind] - heights[ind - 1]);
            int jumpTwo = INT_MAX;
            // Store minimum energy for this stair
            if (ind > 1)
                jumpTwo = dp[ind - 2] + abs(heights[ind] - heights[ind - 2]);
            dp[ind] = min(jumpOne, jumpTwo); 
        }
        // Return the minimum energy required to reach the last stair
        return dp[n - 1]; 
    }
};

int main() {
    vector<int> heights = {30, 10, 60, 10, 60, 50};
    Solution sol;
    cout << sol.frogJump(heights) << endl; // Output the result
    return 0;
}

Complexity Analysis:

• Time Complexity: O(n), where n is the number of stairs.
• Space Complexity: O(n), due to the storage required for the dp array.

4️⃣ Space Optimized

Intuition:

To solve the problem of finding the minimum energy required for a frog to jump from the first to the last stair using a space-optimized approach, the key is to recognize that only the last two computed values are needed at any iteration. This realization allows the solution to avoid maintaining an entire array, thus saving space.

In this approach, instead of storing all computed energy values in an array, the focus is on keeping track of only the most recent two values. Specifically, the energy required to reach the current stair is determined using the energy values from the previous two stairs. This approach simplifies memory usage while maintaining the correctness of the solution. By iteratively updating two variables that represent the energy values of the last two stairs, the minimum energy can be computed efficiently.

Approach:

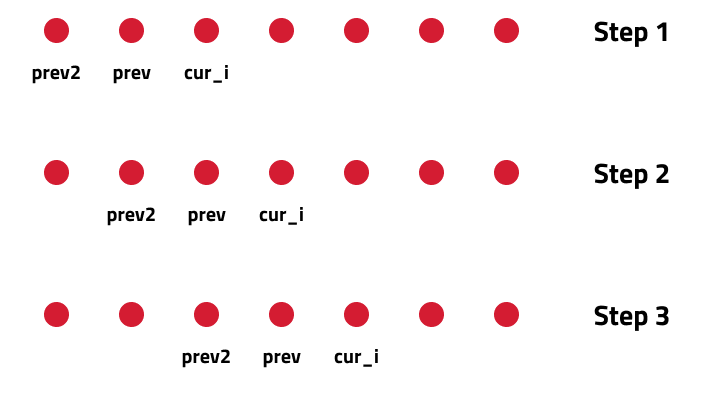
• Initialize Variables:
  • prev: Represents the energy required to reach the previous stair.
  • prev2: Represents the energy required to reach the stair before the previous one.
• Iterative Calculation:
  • For each stair from the second to the last, compute the energy required based on the values of prev and prev2.
  • Update prev and prev2 for the next iteration.

Code:

#include<bits/stdc++.h>
using namespace std;

class Solution {
public:
    int frogJump(vector<int>& heights) {
        int n = heights.size();
        int prev = 0, prev2 = 0; // Initialize for base cases

        // Iterative calculation
        for (int i = 1; i < n; i++) {
            int jumpOne = prev + abs(heights[i] - heights[i - 1]);
            int jumpTwo = INT_MAX;
            if (i > 1)
                jumpTwo = prev2 + abs(heights[i] - heights[i - 2]);
            // Minimum energy for current stair    
            int cur_i = min(jumpOne, jumpTwo); 
            // Update previous values
            prev2 = prev; 
            prev = cur_i;
        }
        // Return the minimum energy required to reach the last stair
        return prev; 
    }
};

int main() {
    vector<int> heights = {30, 10, 60, 10, 60, 50};
    Solution sol;
    cout << sol.frogJump(heights) << endl; // Output the result
    return 0;
}

Complexity Analysis:

• Time Complexity: O(n), where n is the number of stairs.
• Space Complexity: O(1), as only two variables are used to store the last two energy values.