Problem Statement

We are given two non-empty linked list representing two non-negative integers. The digits are stored in reverse order, and each node contains a single digit. We need to add the two numbers and return the sum as a linked list.

Examples

Example 1:

Input: List1 = [2, 4, 3], List2 = [5, 6, 4]
Result: sum = 807; List = [7, 0, 8]

Explanation: Since the digits are stored in reverse order, reverse the number first to get the original number and then add them as 342 + 465 = 807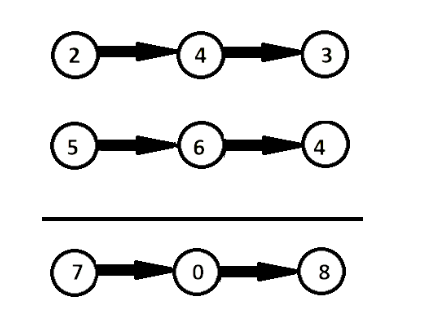

Different Approaches

1️⃣ Elementary Math

Keep track of the carry using a variable and simulate digits-by-digits sum starting from the head of the list, which contains the least significant digit.

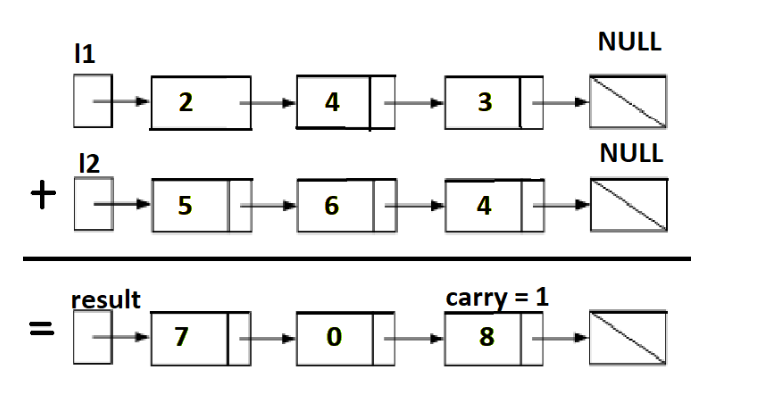
Algorithm:

• Create a dummy node which is the head of new linked list.
• Create a node temp, initialize it with dummy.
• Initialize carry to 0.
• Loop through lists l1 and l2 until you reach both ends, and until carry is present.
  • Set sum = l1.val + l2.val
  • Update carry = sum/10
  • Create a new node with the digit value of (sum%10) and set it to temp node's next, then advance temp node to next.
  • Advance both l1 and l2.
• Return dummy's next node.

Code:

#include <iostream>
using namespace std;

// Definition of the ListNode structure
struct ListNode {
    int val;                // Value of the node
    ListNode *next;         // Pointer to the next node in the list
    // Constructor to initialize a node with a value
    ListNode(int x) : val(x), next(nullptr) {}
};

// Function to add two numbers represented as linked lists
ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {
    // Create a dummy node to simplify list construction
    ListNode* dummy = new ListNode(0);
    ListNode* current = dummy; // Pointer to track the current position in the result list
    int carry = 0;             // To handle carry-over during addition

    // Loop until both lists are fully traversed and there's no carry left
    while (l1 || l2 || carry) {
        int sum = carry;       // Start with the carry from the previous step
        
        // Add the value of the current node of l1 if it exists
        if (l1) {
            sum += l1->val;
            l1 = l1->next;     // Move to the next node in l1
        }
        
        // Add the value of the current node of l2 if it exists
        if (l2) {
            sum += l2->val;
            l2 = l2->next;     // Move to the next node in l2
        }
        
        carry = sum / 10;      // Compute the carry for the next digit
        current->next = new ListNode(sum % 10); // Create a new node for the current digit of the sum
        current = current->next;               // Move to the next position in the result list
    }

    return dummy->next;        // Return the head of the resulting list (skipping the dummy node)
}

// Utility function to print a linked list
void printList(ListNode* head) {
    while (head) {
        cout << head->val << " ";  // Print the value of the current node
        head = head->next;         // Move to the next node
    }
    cout << endl;
}

int main() {
    // Creating the first linked list: 2 -> 4 -> 3 (represents the number 342)
    ListNode* l1 = new ListNode(2);
    l1->next = new ListNode(4);
    l1->next->next = new ListNode(3);

    // Creating the second linked list: 5 -> 6 -> 4 (represents the number 465)
    ListNode* l2 = new ListNode(5);
    l2->next = new ListNode(6);
    l2->next->next = new ListNode(4);

    // Printing the input lists
    cout << "List 1: ";
    printList(l1);
    cout << "List 2: ";
    printList(l2);

    // Adding the two numbers represented by the linked lists
    ListNode* sumList = addTwoNumbers(l1, l2);

    // Printing the resulting sum list
    cout << "Sum: ";
    printList(sumList);

    return 0;
}

// Output
List 1: 2 4 3 
List 2: 5 6 4 
Sum: 7 0 8 

Complexity Analysis:

• Time Complexity: O(max (m,n))
  • m and n represent the length of l1 and l2 respectively.
• Space Complexity: O(max(m, n))
  • The length of the new lists is at most max(m, n) +1