Problem Statement
Given the root node of a binary search (BST) and a value val to insert into the tree. Return the root node of the BST after the insertion.
It is guaranteed that the new value does not exist in the original BST. Note that the compiler output shows true if the node is added correctly, else false.
Examples
Example 1:
Input: root = [4, 2, 7, 1, 3], val = 5
Output: [4, 2, 7, 1, 3, 5]
Explanation: Below is the image of the BST after insertion of node.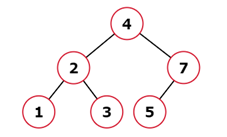
There is another way to insert the given value node as shown in the pic below:
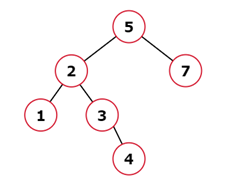
Example 2:
Input: root = [40, 20, 60, 10, 30, 50, 70], val = 25
Output: [40, 20, 60, 10, 25, 50, 70, null, null, null, 30]
Explanation: The BST is given below after insertion.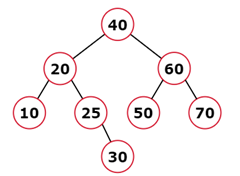
Different Approaches
1️⃣ Iterative
Code:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int data;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int val) : data(val), left(nullptr), right(nullptr) {}
* };
**/
class Solution {
public:
TreeNode* insertIntoBST(TreeNode* root, int valueToInsert) {
// Step 1: If the tree is empty, create a new node and return it as the root
if (root == nullptr) {
return new TreeNode(valueToInsert);
}
// Step 2: Start from the root and find the correct position to insert the new node
TreeNode* current = root;
while (true) {
if (valueToInsert > current->data) {
// Step 3a: Go to the right subtree if value is greater than current node
if (current->right == nullptr) {
// Step 3b: If right child is empty, insert here
current->right = new TreeNode(valueToInsert);
break;
} else {
// Continue traversing right
current = current->right;
}
} else {
// Step 4a: Go to the left subtree if value is less than or equal to current node
if (current->left == nullptr) {
// Step 4b: If left child is empty, insert here
current->left = new TreeNode(valueToInsert);
break;
} else {
// Continue traversing left
current = current->left;
}
}
}
// Step 5: Return the original root after insertion
return root;
}
};
2️⃣ Recursive Approach
Intuition:
The goal is to insert a new value into a Binary Search Tree (BST) while ensuring that the fundamental properties of the BST are preserved. A BST is organized in such a way that for any given node, all values in its left subtree are smaller than the node's value, and all values in the right subtree are larger. The insertion process requires identifying the correct location for the new value, ensuring that the tree remains correctly ordered. This involves traversing the tree, making comparisons at each node, and ultimately finding an appropriate null child position where the new node can be inserted, thereby maintaining the structure and properties of the BST.
Approach:
- Initiate a traversal of the tree to locate the correct insertion point by comparing the value to be inserted with the value of the current node.
- If the value to be inserted is less than the value of the current node, proceed to explore the left subtree.
- If the value to be inserted is greater than the value of the current node, proceed to explore the right subtree.
- Continue this comparison and traversal process until a potential leaf position (a null child) is identified in the relevant subtree.
- To insert the new value, create a new node containing the given value, and attach this new node as a child of the parent node at the empty position found in the previous step. If the value is less than the parent's node value, the new node should be attached as the left child; otherwise, it should be attached as the right child.
- Return the updated Binary Search Tree, now including the newly inserted value while maintaining its properties.
Code:
#include <bits/stdc++.h>
using namespace std;
// Definition for a binary tree node.
class TreeNode {
public:
int data;
TreeNode* left;
TreeNode* right;
TreeNode(int val) : data(val), left(nullptr), right(nullptr) {}
};
class Solution {
private:
// Recursive function to insert a value into the BST
TreeNode* solve(TreeNode* node, int val) {
// If the current node is NULL, create a new TreeNode with the given value
if (node == nullptr) {
return new TreeNode(val);
}
// Traverse the tree to find the correct insertion point
if (val < node->data) {
// Move to the left subtree
node->left = solve(node->left, val);
} else if (val > node->data) {
// Move to the right subtree
node->right = solve(node->right, val);
}
// Return the (potentially modified) node
return node;
}
public:
// Public method to start the insertion process
TreeNode* insertIntoBST(TreeNode* root, int val) {
return solve(root, val);
}
// Helper function to print the tree in-order
void printInOrder(TreeNode* root) {
if (root == nullptr) return;
printInOrder(root->left);
cout << root->data << " ";
printInOrder(root->right);
}
};
// Main function for testing
int main() {
Solution solution;
// Create a sample BST: [4, 2, 7, 1, 3]
TreeNode* root = new TreeNode(4);
root->left = new TreeNode(2);
root->right = new TreeNode(7);
root->left->left = new TreeNode(1);
root->left->right = new TreeNode(3);
int val = 5;
// Insert the value into the BST
TreeNode* newRoot = solution.insertIntoBST(root, val);
// Print the BST in-order to verify the insertion
solution.printInOrder(newRoot); // Output should be: 1 2 3 4 5 7
cout << endl;
// Clean up memory (optional, but recommended for large trees)
// In practice, you would need a function to delete all nodes to avoid memory leaks
return 0;
}
Complexity Analysis:
- Time Complexity:
O(H), where H is the height of the tree, which in the worst case can be N (for a skewed tree), but for a balanced BST, it will be log(N). - Space Complexity:
O(1)Only a constant amount of space is used to store the current node and the new node, regardless of the size of the input tree.
