Problem Statement:

You are given a 2D integer array image representing an image, and three integers sr, sc, and newColor. The integer sr represents the row index, and sc represents the column index of the starting pixel. The task is to flood fill the image starting from the pixel at (sr, sc) by replacing the pixel’s color, and all connected pixels (horizontally or vertically) of the same color, with the given newColor.

Input:

• A 2D array image representing the image where image[i][j] is the pixel value.
• Two integers sr and sc representing the starting row and column of the flood fill.
• An integer newColor representing the color to be applied.

Output:

• Return the modified 2D array after performing the flood fill.

Constraints:

• The number of rows and columns in the image is within the range [1, 50].
• The pixel values of the image are within the range [0, 65535].
• 0 <= sr < image.length.
• 0 <= sc < image[0].length.

Examples

Example 1:

Input: image = [
                [1, 1, 1],
                [1, 1, 0],
                [1, 0, 1]
               ]
       sr = 1, sc = 1, newColor = 2
       
Output: [
         [2, 2, 2],
         [2, 2, 0],
         [2, 0, 1]
        ]

Explanation:
The pixel at position (1,1) has value 1. All 4-directionally connected pixels with the same value 1 are filled with 2.

Example 2:

Input: image = [
                [0, 1, 0],
                [1, 1, 0],
                [0, 0, 1]
               ]
       sr = 2, sc = 2, newColor = 3
       
Output: [
         [0, 1, 0],
         [1, 1, 0],
         [1, 0, 3]
        ]

Explanation:
Starting from the pixel at position (2, 2) (i.e., the blue pixel), we flood fill all adjacent pixels that have the same color as the starting pixel. In this case, only the pixel at position (2, 2) itself is of the same color. So, only that pixel gets colored with the new color, resulting in the updated image.

Theory

The problem can be visualized as a graph traversal problem where:

• Each pixel is a node.
• Each node is connected 4-directionally (up, down, left, right) to its neighboring pixels if they share the same color.

We are tasked to traverse all nodes connected to the starting node that have the same initial color, and change their color to newColor.

The traversal can be done using either Depth-First Search (DFS) or Breadth-First Search (BFS).

Different Approach

1️⃣ DFS

Intuition:

How to solve this problem using a graph?

Think of all the pixels in the image as nodes or vertices which are connected through each other via 4 edges.

Given the starting pixel, any traversal algorithm can be used to find all the neighbors having similar pixel value. During the traversal, each pixel value can be changed to the new color value to get the flood filled image.

How to traverse the neighbors efficiently?

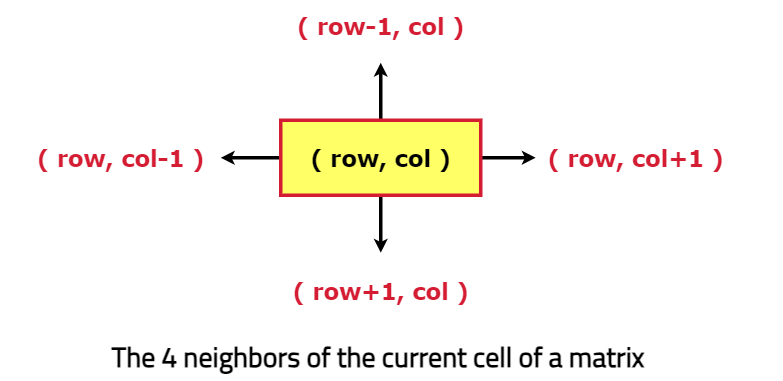
The 4 neighbors of the current cell can be shown like this:

                        +-----------------------+
                        |   (row - 1, column)   |
+-----------------------+-----------------------+-----------------------+
|   (row, column - 1)   |     (row, column)     |   (row, column + 1)   |
+-----------------------+-----------------------+-----------------------+
                        |   (row + 1, column)   |
                        +-----------------------+

The 4 neigbors of the current cell of a matrix.

For efficient traversal of all neighboring pixels, the delRow and delCol arrays can be used where:

• delRow = {-1, 0, 1, 0}
• delCol = {0, 1, 0, -1}

• delRow = {-1, 0, 1, 0}
• delCol = {0, 1, 0, -1}

Approach:

• Initialize a new image to store the image after flood fill. (The given image can be used for the same but it is considered a good practice if the given input is not altered.)
• To navigate to the neighboring pixels, direction vectors are defined for moving up, right, down, and left. A helper function checks if a pixel is within the bounds of the image. This ensures that the traversal does not go out of the image boundary.
• Starting from the given pixel, a recursive DFS traversal is performed during which all the pixels having same initial color are marked with new color in the new image.
• Once the traversal terminates, the new image stores the flood filled image.

Code:

#include <bits/stdc++.h>
using namespace std;

class Solution {
private:
    // DelRow and delCol for neighbors
    vector<int> delRow = {-1, 0, 1, 0};
    vector<int> delCol = {0, 1, 0, -1};
    
    /* Helper Function to check if a 
    pixel is within boundaries */
    bool isValid(int &i, int &j, 
                 int &n, int &m) {
        
        // Return false if pixel is invalid
        if(i < 0 || i >= n) return false;
        if(j < 0 || j >= m) return false;
        
        // Return true if pixel is valid
        return true;
    }
    
    // Function to perform DFS traversal 
    void dfs(int row, int col, vector<vector<int>>&ans,
             vector<vector<int>>& image, int newColor,
             int iniColor) {
                 
        // color with new color
        ans[row][col] = newColor; 
        
        // Getting the dimensions of image
        int n = image.size();
        int m = image[0].size(); 
        
        // Traverse the 4 neighbors
        for(int i=0; i < 4; i++) {
            
            // Coordinates of new pixel
            int nrow = row + delRow[i]; 
            int ncol = col + delCol[i]; 
            
            /* check for valid, unvisited pixels
            having same initial color */
             
            if(isValid(nrow, ncol, n, m) && 
               image[nrow][ncol] == iniColor 
               && ans[nrow][ncol] != newColor) {
                
                // Recursively perform DFS 
                dfs(nrow, ncol, ans, image, 
                   newColor, iniColor); 
            }
        }
    }
    
public:
    // Function to perform flood fill algorithm 
    vector<vector<int>> floodFill(vector<vector<int>> &image,
                                  int sr, int sc, int newColor) {
        
        // Store initial color
        int iniColor = image[sr][sc]; 
        
        // To store the updated image
        vector<vector<int>> ans = image; 
        
        // Start DFS traversal from start cell
        dfs(sr, sc, ans, image, newColor, iniColor); 
        
        // Return the answer image
        return ans; 
    }
};

int main() {
    vector<vector<int>> image = {
	    {1,1,1},
	    {1,1,0},
	    {1,0,1}
	};
    int sr = 1, sc = 1;
    int newColor = 2;
    
    int n = image.size();
    int m = image[0].size();
    
    /* Creating an instance of 
    Solution class */
    Solution sol; 
    
    /* Function call to find the 
    number of islands in given grid*/
    vector<vector<int>> ans = sol.floodFill(image, sr, sc, newColor);
    
    cout << "Image after performing flood fill algorithm: \n\n";
    
    for(int i=0; i < n; i++) {
        for(int j=0; j < m; j++) {
            cout << ans[i][j] << " "; 
        }
        cout << endl;
    }
    
    return 0;
}

Complexity Analysis:

• Time Complexity: O(N*M), (where N and M are the dimensions of image).
  • In the worst case, all the pixel will have same color, DFS call will made for N*M nodes.
  • For every pixel, its four neighbors are traversed, taking O(4*N*M) time.
• Space Complexity: O(N*M)
  • Extra space for the new image takes O(N*M) space.
  • Recursive stack space for DFS calls will take at most O(N*M) space.