Problem Statement
Given a chain of matrices A1, A2, A3,.....An, you have to figure out the most efficient way to multiply these matrices. In other words, determine where to place parentheses to minimize the number of multiplications.
Given an array nums of size n. Dimension of matrix Ai ( 0 < i < n ) is nums[i - 1] x nums[i].Find a minimum number of multiplications needed to multiply the chain.
Examples
Example 1:
Input: nums = [10, 15, 20, 25]
Output : 8000
Explanation : There are two ways to multiply the chain - A1*(A2*A3) or (A1*A2)*A3.
A1 = 10*15
A2 = 15*20
A3 = 20*25
If we multiply in order- A1*(A2*A3), then number of multiplications required are 11250.
If we multiply in order- (A1*A2)*A3, then number of multiplications required are 8000.
Thus minimum number of multiplications required is 8000.Example 2:
Input: nums = [40, 20, 30, 10, 30]
Output: 26000
Explanation: It has four matrices:
A1 = 40*20
A2 = 20*30
A3 = 30*10
A4 = 10*30
Possible ways to multiple matrices:
((A1 * A2) * A3) * A4)Different Approaches
1️⃣ Recursive Approach
Identification:
Whenever we need to find the answer to a large problem such that the problem can be broken into subproblems and the final answer varies due to the order in which the subproblems are solved, we can think in terms of partition DP.
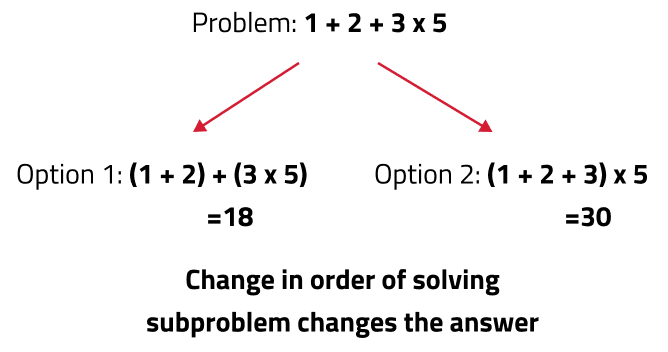
Matrix Chain Multiplication:
Let us first understand the problem of matrix chain multiplication. In order to understand the problem we need to first understand the rules of matrix multiplication:
Two matrices A1 and A2 of dimensions [p x q] and [r x s] can only be multiplied if and only if q=r.
The total number of multiplications required to multiply A1 and A2 are: p*q*s
Understanding:
As this problem of matrix multiplication solves one big problem ( minimum operations to get A1.A2….An) and the answer varies in the order the subproblems are being solved, we can identify this problem of pattern partition DP.
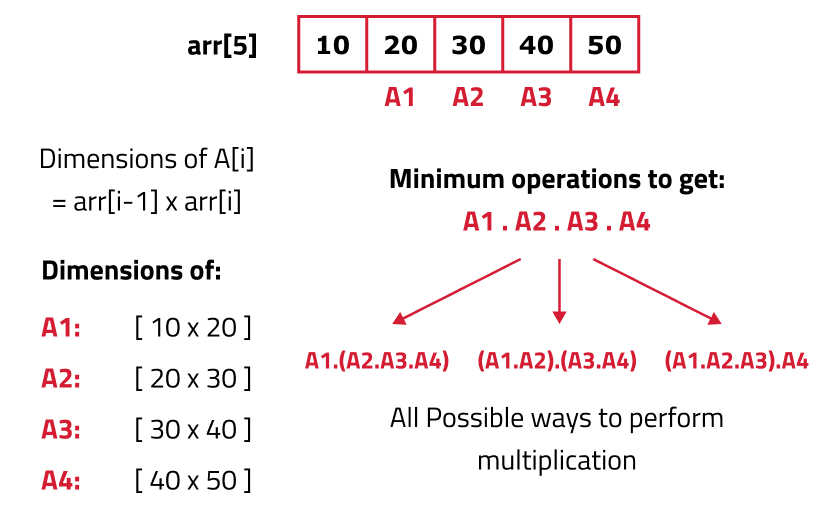
Rules to solve the problem of partition DP:
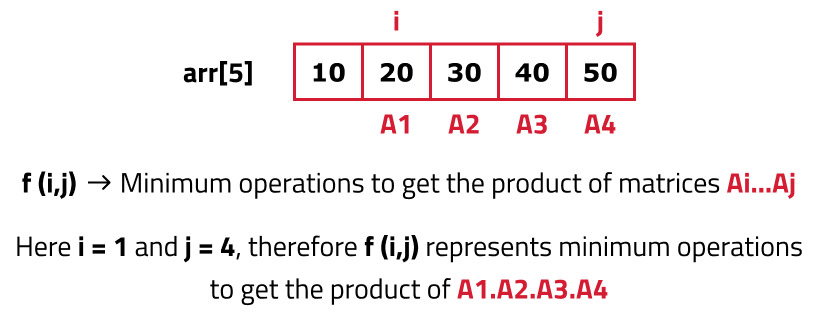
Start with the entire block/array and mark it with i,j: We are given an array, which can be represented by 'i' and 'j' as shown in the image below.
Try out all partitions: Let us first analyze all the partitions that can be made with respect to the indexing.
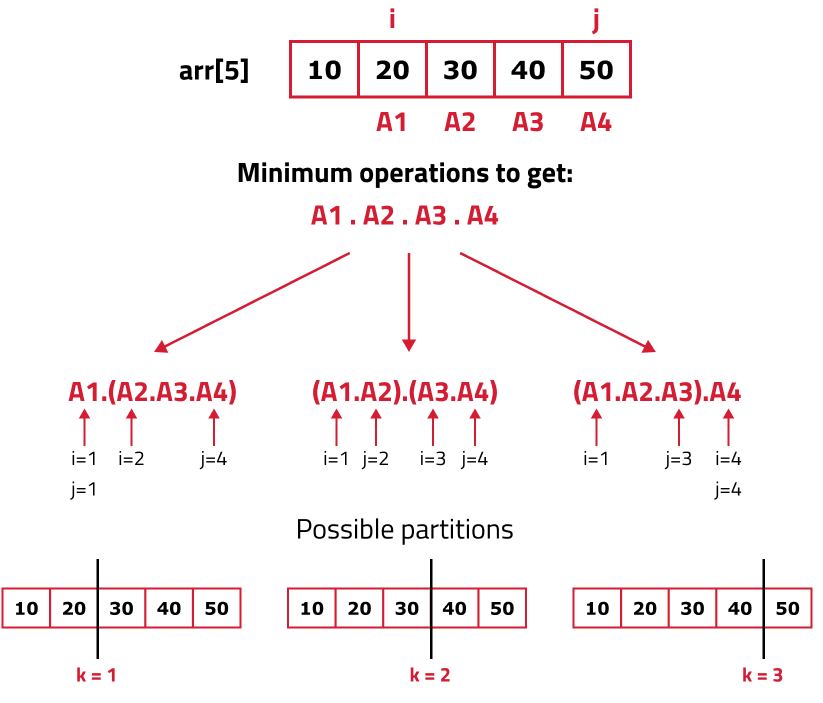
As we can see 3 partitions are possible, to try all three partitions, initialize a for loop starting from 'i' and ending at (j-1), (1 to 3) in this case. The two partitions will be f(i,k) and f(k+1,j).
- Base Case: If i==j, it means we are interested in a single matrix and no operation is required to multiply it so return 0.
Run the best possible answer of the two partitions: Answer that comes after dividing the problem into two subproblems and solving them recursively. Let's understand this by the help of an example.
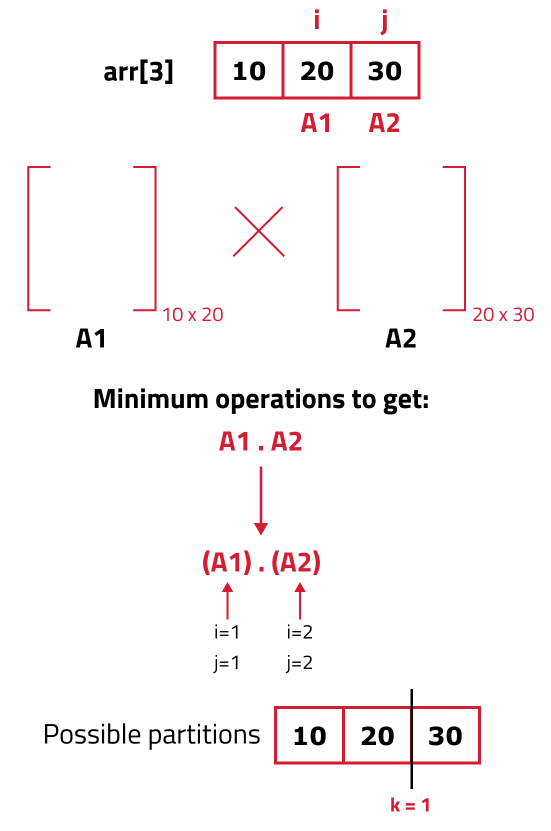
As there are only two matrices, we can say that only one partition is possible at k=1, when we do this partition, we see that the two partitions made are f(1,1) and f(2,2) (by f(i,k) and f(k+1,j) therefore we hit the base condition in both of these subcases which return 0.
Now, we know that the subproblems/partitions give us 0 operations, but we still have some work to do. The partition f(i,k) gives us a resultant matrix of dimensions [i -1 x k] and the partition f(k+1,j) gives us a resultant matrix of dimensions [k,j]. Therefore we need to count the number of operations for our two partitions (k=1) as shown:
Now, this is at one partition, in general, we need to calculate this answer of every partition and return the minimum as the answer.
To summarize:
- Represent the entire array by two indexes i and j. In this question i =1 and j = n. We need to find f(i,j).
- Maintain a 'mini' variable to get the minimum answer.>/li>
- Set a for loop to find the answer( variable k) from i to j-1. In every iteration find the answer, with the formula discussed above and compare it with the 'mini' value.
- Finally, return the 'mini' variable as the answer.
Code:
#include <bits/stdc++.h>
using namespace std;
class Solution{
private:
/* Recursive function to compute the
minimum cost of matrix multiplication*/
int func(vector<int>& arr, int i, int j) {
/* Base case: When there is only one
matrix, no multiplication is needed*/
if (i == j)
return 0;
int mini = INT_MAX;
// Partition the matrices between i and j
for (int k = i; k <= j - 1; k++) {
/* Compute the cost of multiplying matrices
from i to k and from k+1 to j and add cost
of multiplying the two resulting matrices*/
int ans = func(arr, i, k) + func(arr, k + 1, j) + arr[i - 1] * arr[k] * arr[j];
// Update the minimum cost
mini = min(mini, ans);
}
// Return the minimum cost found
return mini;
}
public:
/* Function to set up the parameters
and call the recursive function*/
int matrixMultiplication(vector<int>& nums) {
int N = nums.size();
// Starting index of the matrix chain
int i = 1;
// Ending index of the matrix chain
int j = N - 1;
// Call the recursive function
return func(nums, i, j);
}
};
int main() {
vector<int> arr = {10, 20, 30, 40, 50};
//Create an instance of Solution class
Solution sol;
// Print the result
cout << "The minimum number of operations is " << sol.matrixMultiplication(arr);
return 0;
}
Complexity Analysis:
- Time Complexity: Exponential.
- Space Complexity: O(N), As we are using auxiliary stack space.
2️⃣ Memoization
If we draw the recursion tree, we will see that there are overlapping subproblems. Hence the DP approaches can be applied to the recursive solution.
In order to convert a recursive solution to memoization the following steps will be taken:
- Declare a dp array of size [n][n]: As there are two changing parameters in the recursive solution, 'i' and 'j'. The maximum value 'i' and 'j' can attain is (n), where n is the size of array. Therefore, we need 2D dp array.
- The dp array stores the calculations of subproblems. Initialize dp array with -1, to indicate that no subproblem has been solved yet.
- While encountering an overlapping subproblem: When we come across a subproblem, for which the dp array has value other than -1, it means we have found a subproblem which has been solved before hence it is an overlapping subproblem. No need to calculate it's value again just retrieve the value from dp array and return it.
- Store the value of subproblem: Whenever, a subproblem is encountered and it is not solved yet(the value at this index will be -1 in the dp array), store the calculated value of subproblem in the array.
Code:
#include <bits/stdc++.h>
using namespace std;
class Solution{
private:
/* Recursive function to compute the
minimum cost of matrix multiplication*/
int func(vector<int>& arr, int i, int j, vector<vector<int>>& dp) {
/* Base case: When there is only one
matrix, no multiplication is needed*/
if (i == j)
return 0;
//Check if the subproblem is already calculated
if(dp[i][j]!=-1)
return dp[i][j];
int mini = INT_MAX;
// Partition the matrices between i and j
for (int k = i; k <= j - 1; k++) {
/* Compute the cost of multiplying matrices
from i to k and from k+1 to j and add cost
of multiplying the two resulting matrices*/
int ans = func(arr, i, k, dp) + func(arr, k + 1, j, dp) + arr[i - 1] * arr[k] * arr[j];
// Update the minimum cost
mini = min(mini, ans);
}
// Store and return the minimum cost found
return dp[i][j] = mini;
}
public:
/* Function to set up the parameters
and call the recursive function*/
int matrixMultiplication(vector<int>& nums) {
int N = nums.size();
// Starting index of the matrix chain
int i = 1;
// Ending index of the matrix chain
int j = N - 1;
vector<vector<int>> dp(N,vector<int>(N,-1));
// Call the recursive function
return func(nums, i, j, dp);
}
};
int main() {
vector<int> arr = {10, 20, 30, 40, 50};
//Create an instance of Solution class
Solution sol;
// Print the result
cout << "The minimum number of operations is " << sol.matrixMultiplication(arr);
return 0;
}
Complexity Analysis:
- Time Complexity:
O(N*N*N), There are N*N states and we explicitly run a loop inside the function which will run for N times, therefore at max ‘N*N*N’ new problems will be solved. - Space Complexity:
O(N*N) + O(N). We are using an auxiliary recursion stack space O(N) and a 2D array O(N*N).