Problem Statement

Given the root node of a binary search tree (BST) and a value key. Return the root node of the BST after the deletion of the node with the given key value.

Note: As there can be many correct answers, the compilers returns true if the answer is correct, otherwise false.

Examples

Example 1:

Input: root = [5, 3, 6, 2, 4, null, 7], key = 3
Output: [5, 4, 6, 2, null, null, 7]

Explanation: Below is the image of the original BST followed by the image after deletion.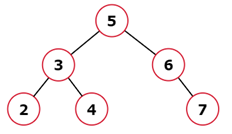

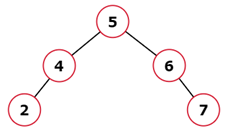
Example 2:

Input: root = [5, 3, 6, 2, 4, null, 7], key = 0
Output: [5, 3, 6, 2, 4, null, 7]

Explanation: The tree does not have the node with value 0.

Different Approaches

1️⃣ 

Intuition:

Deleting a node in a Binary Search Tree (BST) requires addressing various scenarios based on the node's children. If the node has no children, it can be simply removed. If the node has one child, it is replaced by its single child. If the node has two children, the challenge is to maintain the BST properties. The node must be replaced by its in-order successor (the smallest node in the right subtree), which ensures the structure remains valid. The key task is to adjust the pointers of the parent node to reflect these changes, ensuring the integrity of the BST.

Approach:

1. Implement a helper function, connector, to manage the replacement of a node with one or two children.
2. Within the connector function:
   1. If the node has no left child, return the right child. This effectively removes the node while preserving the right subtree.
   2. If the node has no right child, return the left child. This preserves the left subtree while removing the node.
   3. If the node has both left and right children, locate the leftmost node in the right subtree (the in-order successor). Attach the left subtree of the node to be deleted to this leftmost node.
   4. Return the right child of the node to be deleted as the new root of the subtree.
3. Within the deleteNode function:
   1. Handle the case where the tree is empty by returning None.
   2. If the root node matches the key to be deleted, invoke the connector function to handle the replacement.
   3. Traverse the tree to locate the node with the specified key while adhering to BST properties. Adjust pointers accordingly to remove the node and preserve the BST structure.
   4. Apply the connector function to the found node to complete its deletion and return the modified tree.

Code:

#include <bits/stdc++.h>
using namespace std;

// Definition for a binary tree node.
struct TreeNode {
    int data;
    TreeNode *left;
    TreeNode *right;
    TreeNode(int x) : data(x), left(nullptr), right(nullptr) {}
};

class Solution {
public:
    // Helper function to connect subtrees after deleting a node
    TreeNode* connector(TreeNode* root) {
        // Case 1: If the node has no left child,
        // return the right subtree to bypass the node.
        if (!root->left)
            return root->right;
        
        // Case 2: If the node has no right child,
        // return the left subtree to bypass the node.
        else if (!root->right)
            return root->left;

        /* 
        Case 3: If the node has both left and right children:
        1. Save the left subtree in a temporary variable.
        2. Find the leftmost node in the right subtree.
        3. Attach the left subtree to the leftmost node in the right subtree. */
        TreeNode* leftchild = root->left;
        TreeNode* leftmost_child_in_right_subtree = root->right;

        // Traverse to the leftmost node in the right subtree.
        while (leftmost_child_in_right_subtree->left) {
            leftmost_child_in_right_subtree =
                leftmost_child_in_right_subtree->left;
        }

        // Attach the left subtree to the leftmost node in the right subtree.
        leftmost_child_in_right_subtree->left = leftchild;

        // Return the right subtree as the new root of the modified tree.
        return root->right;
    }

    // Function to delete a node with a specific key from the binary search tree
    TreeNode* deleteNode(TreeNode* root, int key) {
        // Base case: if the tree is empty, return NULL.
        if (root == NULL)
            return NULL;

        // If the node to be deleted is the root node,
        // use the connector function to replace the root.
        if (root->data == key) {
            return connector(root);
        }

        // Traverse the tree to find the node to be deleted.
        TreeNode* node = root;
        while (node) {
            // If the key to be deleted is smaller than the current node's data,
            // move to the left subtree.
            if (node->data > key) {
                // If the left child is the node to be deleted,
                // update the left child with the connector function.
                if (node->left && node->left->data == key) {
                    node->left = connector(node->left);
                    break;
                } else {
                    node = node->left; 
                }
            }
            // If the key to be deleted is larger than the current node's data,
            // move to the right subtree.
            else {
                // If the right child is the node to be deleted,
                // update the right child with the connector function.
                if (node->right && node->right->data == key) {
                    node->right = connector(node->right);
                    break;
                } else {
                    node = node->right; 
                }
            }
        }

        // Return the modified tree with the node deleted.
        return root;
    }
};

int main() {
    // Create a sample binary search tree.
    TreeNode* root = new TreeNode(5);
    root->left = new TreeNode(3);
    root->right = new TreeNode(8);
    root->left->left = new TreeNode(2);
    root->left->right = new TreeNode(4);

    Solution sol;
    // Delete node with key 3 from the tree.
    root = sol.deleteNode(root, 3);

    return 0;
}

Complexity Analysis:

• Time Complexity:O(H), explanation is that the time complexity is dependent on the height of the tree.
• Space Complexity:O(H), explanation is that the maximum depth of the recursion call stack is equal to the height of the tree.