Problem Statement
Given an array arr of n integers, partition the array into two subsets such that the absolute difference between their sums is minimized.
Examples
Example 1:
Input: arr = [1, 7, 14, 15]
Output: 1
Explanation: The array can be partitioned as [1, 7, 5] and [14], with an absolute difference of 1.Example 2:
Input: arr = [3, 1, 6, 2, 2]
Output: 0
Explanation: The array can be partitioned as [3, 2, 2] and [6, 1], with an absolute difference of 0.Different Approaches
1️⃣ Recursive Approach
This question is a slight modification of the problem discussed in the Subset Sum equal to target. Before discussing the approach for this question, it is important to understand what we did in the previous question of the Subset Sum equal to the target. There we found whether or not a subset exists in an array with a given target sum.
In this question, we need to partition the array into two subsets( say with sum S1 and S2) and we need to return the minimized absolute difference of S1 and S2. But do not need two variables for it. We can use a variable 'totSum', which stores the sum of all elements of the input array, and then we can simply say S2 = totSum - S1. Therefore we only need one variable S1.
From here try to find a subset in the array with a target as discussed in Subset Sum equal to the target.
Steps to form the recursive solution:
- Express the problem in terms of indexes: The array will have an index but there is one more parameter “target”. So, we can say that initially, we need to find(n-1, target) which means that we need to find whether there exists a subset in the array from index 0 to n-1, whose sum is equal to the target.
- So, f(ind, target) will check whether a subset exists in the array from index 0 to index 'ind' such that the sum of elements is equal to the target.
- Try out all possible choices at a given index: As all the subsets needs to be generated, we will use the pick/non-pick technique.There will be two choices in each function call:
- Do not include the current element in the subset: First try to find a subset without considering the current index element. For this, make a recursive call to f(ind-1,target).
- Include the current element in the subset: Now try to find a subset by considering the current index element as part of subset. As the current element(arr[ind]) is included, the remaining target sum will be target - arr[ind]. Therefore, make a function call of f(ind-1,target-arr[ind]).
Note: Consider the current element in the subset only when the current element is less or equal to the target.
/*It is pseudocode and it is not tied to
any specific programming language*/
f(ind, target){
not pick = f(ind-1, target)
pick = false
if(target <= arr[ind]){
pick = f(ind-1, target - arr[ind])
}
}- Return (pick || not pick): As we are looking for only one subset whose sum of elements is equal to target, if any of the one among 'pick' or 'not pick' returns true, it means the required subset is found so, return true.
/*It is pseudocode and it is not tied to
any specific programming language*/
f(ind, target){
not pick = f(ind-1, target)
pick = false
if(target <= arr[ind]){
pick = f(ind-1, target - arr[ind])
}
return (pick || not pick)
}- Base cases: There will be two base cases.
- First, when target == 0, it means that the subset is already found from the previous steps, so simply return true.
- Another, when ind==0, it means we are at the first element, so return arr[ind]==target. If the element is equal to the target it will return true else false.
Intuition:
The goal is to divide the given array into two subsets such that the absolute difference between their sums is minimized. To achieve this, we leverage the concept of the Subset Sum Problem, where we determine if a subset with a particular sum exists.
- Subset Sum Problem:
Given an array, check if a subset exists with a specific target sum. Here, we compute all subset sums that can be formed by including or excluding elements. - Key Observation:
If the total sum of the array istotalSum, and one subset has a sumsubsetSum, the other subset's sum istotalSum - subsetSum.
Therefore, the absolute difference between the two subsets is: - Minimizing the Difference:
- Generate all possible subset sums (
subsetSum). - For each
subsetSum, compute the corresponding absolute difference. - Track the minimum difference.
- Generate all possible subset sums (
Approach:
- Total Sum Calculation:
- Compute the total sum of all elements in the array:
totalSum.
- Compute the total sum of all elements in the array:
- Subset Sum Check:
- Use a recursive function to determine if a subset with a given
targetSumcan be formed:- Include the current element in the subset (reduce
targetSum). - Exclude the current element and move to the next.
- Include the current element in the subset (reduce
- Use a recursive function to determine if a subset with a given
- Iterate Over Subset Sums:
- Iterate over all possible values of
subsetSumfrom0tototalSum. - For each valid subset sum:
Calculate the difference using the formula:
Difference = |subsetSum - (totalSum - subsetSum)|- Update the minimum difference.
- Iterate over all possible values of
- Return the Result:
- Return the minimum absolute difference encountered.
Dry Run:
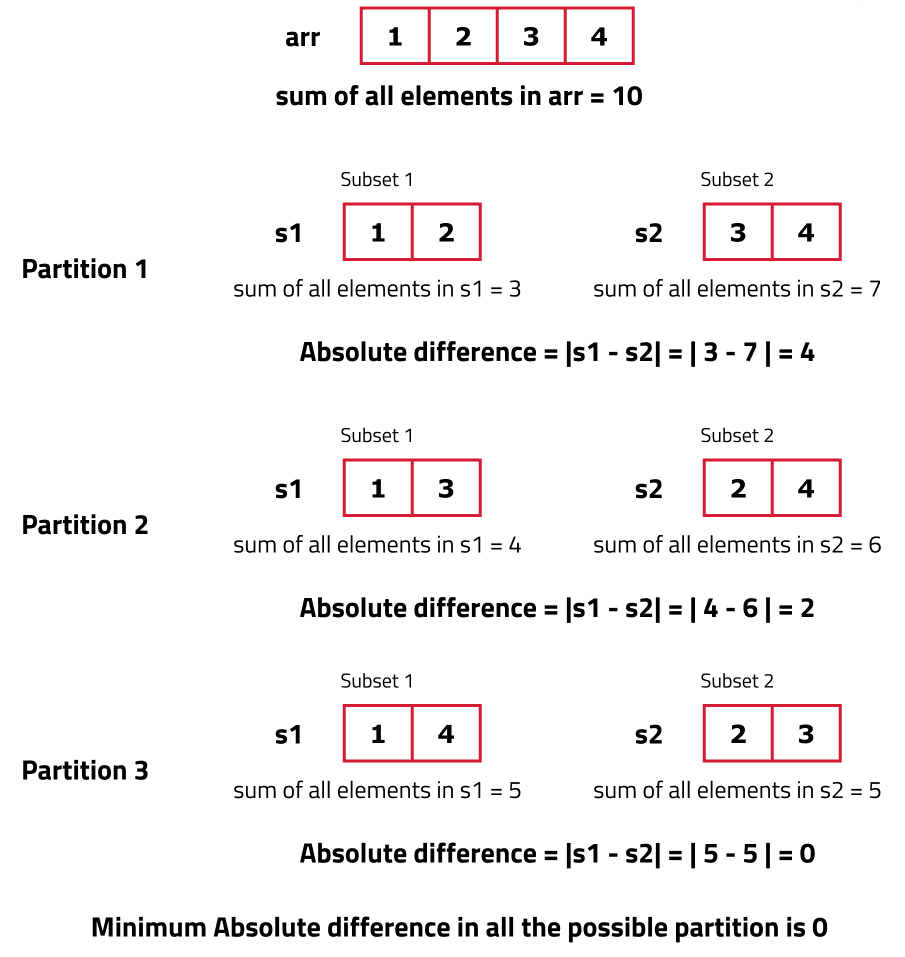
Input:
nums = {1, 2, 3, 4}
Step 1: Total Sum Calculation:
totalSum = 1 + 2 + 3 + 4 = 10
Step 2: Subset Sum Calculation:
- Generate all possible subsets sums using recursion:
0,1,2,3,4,5,6,7,8,9,10.
Step 3: Minimize the Difference
For each valid subsetSum, calculate the absolute difference:
Subset Sum (subsetSum) | Other Subset Sum (totalSum - subsetSum) | Absolute Difference |
|---|---|---|
| 0 | 10 | 10 |
| 1 | 9 | 8 |
| 2 | 8 | 6 |
| 3 | 7 | 4 |
| 4 | 6 | 2 |
| 5 | 5 | 0 |
| 6 | 4 | 2 |
| 7 | 3 | 4 |
| 8 | 2 | 6 |
| 9 | 1 | 8 |
| 10 | 0 | 10 |
Step 4: Minimum Difference
The minimum absolute difference is 0 when:
subsetSum = 5
otherSubsetSum = 5
Code:
#include <bits/stdc++.h>
using namespace std;
class Solution {
private:
// Recursive function to determine if a subset with a given target sum exists
bool isSubsetSumPossible(int index, int targetSum, vector<int>& nums) {
// Base Case 1: If the target sum is achieved, return true
if (targetSum == 0)
return true;
// Base Case 2: If we have reached the first element
if (index == 0)
return (nums[0] == targetSum);
// Option 1: Exclude the current element
bool excludeCurrent = isSubsetSumPossible(index - 1, targetSum, nums);
// Option 2: Include the current element if it does not exceed targetSum
bool includeCurrent = false;
if (nums[index] <= targetSum)
includeCurrent = isSubsetSumPossible(index - 1, targetSum - nums[index], nums);
// Return true if either including or excluding the current element works
return excludeCurrent || includeCurrent;
}
public:
// Function to find the minimum absolute difference between two subset sums
int minSubsetSumDifference(vector<int>& nums, int n) {
int totalSum = 0;
// Step 1: Calculate the total sum of the array
for (int i = 0; i < n; i++) {
totalSum += nums[i];
}
/* Step 2: Check all possible subset sums from 0 to totalSum.
Use a recursive function to determine if a subset with a given sum exists. */
int minimumDifference = INT_MAX;
for (int subsetSum = 0; subsetSum <= totalSum; subsetSum++) {
if (isSubsetSumPossible(n - 1, subsetSum, nums)) {
// Calculate the sum of the other subset
int otherSubsetSum = totalSum - subsetSum;
// Update the minimum difference
int currentDifference = abs(subsetSum - otherSubsetSum);
minimumDifference = min(minimumDifference, currentDifference);
}
}
return minimumDifference;
}
};
int main() {
vector<int> nums = {1, 2, 3, 4};
int n = nums.size();
// Create an instance of the Solution class
Solution solution;
// Call the function and print the result
cout << "The minimum absolute difference is: " << solution.minSubsetSumDifference(nums, n) << endl;
return 0;
}Simple recursive way
class Solution {
public:
// Recursive helper function to explore all subset combinations
int recursive(vector<int>& arr, int index, int currentSum, int totalSum) {
// Base case: all elements have been considered
if (index == arr.size()) {
// The sum of the second subset is totalSum - currentSum
int s2 = totalSum - currentSum;
// Return the absolute difference between the two subset sums
return abs(currentSum - s2);
}
// Include the current element in the subset (add to currentSum)
int include = recursive(arr, index + 1, currentSum + arr[index], totalSum);
// Exclude the current element from the subset (keep currentSum same)
int exclude = recursive(arr, index + 1, currentSum, totalSum);
// Return the minimum difference obtained from both choices
return min(include, exclude);
}
// Main function to be called
int minDifference(vector<int>& arr, int n) {
// Calculate the total sum of all elements
int totalSum = accumulate(arr.begin(), arr.end(), 0);
// Start recursive exploration from index 0 with currentSum 0
return recursive(arr, 0, 0, totalSum);
}
};Explanation:
- Recursive Function (
isSubsetSumPossible):- Determines whether a subset with a given
targetSumcan be formed using elements up to the givenindex. - Uses two choices at each step:
- Exclude the current element.
- Include the current element if it does not exceed the
targetSum.
- Determines whether a subset with a given
minSubsetSumDifferenceFunction:- Iterates over all possible subset sums (
0tototalSum). - For each valid subset sum (where
isSubsetSumPossiblereturnstrue), calculates the absolute difference between two subsets. - Keeps track of the minimum absolute difference.
- Iterates over all possible subset sums (
Complexity Analysis:
- Time Complexity:
- The recursive function
isSubsetSumPossibleexploresO(2^n)possibilities. - Checking all subset sums from
0tototalSumtakesO(totalSum)iterations. - Overall time complexity:
O(2^n * totalSum).
- The recursive function
- Space Complexity:
- The recursion stack consumes O(n) space for depth of recursion.
2️⃣ Memoization:
If we draw the recursion tree, we will see that there are overlapping subproblems. Hence the DP approaches can be applied to the recursive solution.
In order to convert a recursive solution to memoization the following steps will be taken:
- Declare a dp array of size [n][target+1]: As there are two changing parameters in the recursive solution, 'ind' and 'target'. The maximum value 'ind' can attain is (n), where n is the size of array and for 'target' only values between 0 to target. Therefore, we need 2D dp array.
- The dp array stores the calculations of subproblems. Initialize dp array with -1, to indicate that no subproblem has been solved yet.
- While encountering an overlapping subproblem: When we come across a subproblem, for which the dp array has value other than -1, it means we have found a subproblem which has been solved before hence it is an overlapping subproblem. No need to calculate it's value again just retrieve the value from dp array and return it.
- Store the value of subproblem: Whenever, a subproblem is encountered and it is not solved yet(the value at this index will be -1 in the dp array), store the calculated value of subproblem in the array.
Code:
#include <bits/stdc++.h>
using namespace std;
class Solution {
private:
// Recursive function to determine if a subset with a given target sum exists
bool isSubsetSumPossible(int index, int targetSum, vector<int>& nums, vector<vector<int>>& dp) {
// Base Case 1: If the target sum is achieved, return true
if (targetSum == 0) return true;
// Base Case 2: If we have reached the first element
if (index == 0) return (nums[0] == targetSum);
// If the result has already been computed, return it from dp
if (dp[index][targetSum] != -1) return dp[index][targetSum];
// Option 1: Exclude the current element
bool excludeCurrent = isSubsetSumPossible(index - 1, targetSum, nums, dp);
// Option 2: Include the current element if it does not exceed targetSum
bool includeCurrent = false;
if (nums[index] <= targetSum)
includeCurrent = isSubsetSumPossible(index - 1, targetSum - nums[index], nums, dp);
// Store the result in dp
dp[index][targetSum] = (excludeCurrent || includeCurrent);
return dp[index][targetSum];
}
public:
// Function to find the minimum absolute difference between two subset sums
int minSubsetSumDifference(vector<int>& nums, int n) {
int totalSum = 0;
// Step 1: Calculate the total sum of the array
for (int i = 0; i < n; i++) {
totalSum += nums[i];
}
// Step 2: Create a memoization table initialized to -1
vector<vector<int>> dp(n, vector<int>(totalSum + 1, -1));
// Step 3: Check all possible subset sums from 0 to totalSum.
int minimumDifference = INT_MAX;
for (int subsetSum = 0; subsetSum <= totalSum; subsetSum++) {
if (isSubsetSumPossible(n - 1, subsetSum, nums, dp)) {
// Calculate the sum of the other subset
int otherSubsetSum = totalSum - subsetSum;
// Update the minimum difference
int currentDifference = abs(subsetSum - otherSubsetSum);
minimumDifference = min(minimumDifference, currentDifference);
}
}
return minimumDifference;
}
};
int main() {
vector<int> nums = {1, 2, 3, 4};
int n = nums.size();
// Create an instance of the Solution class
Solution solution;
// Call the function and print the result
cout << "The minimum absolute difference is: " << solution.minSubsetSumDifference(nums, n) << endl;
return 0;
}Or the recursive way
class Solution {
public:
// Recursive function with memoization
int recursive(vector<int>& arr, int index, int currentSum, int totalSum, vector<vector<int>>& dp) {
// Base case: all elements considered
if (index == arr.size()) {
int s2 = totalSum - currentSum;
return abs(currentSum - s2);
}
// If this state was already computed, return it
if (dp[index][currentSum] != -1)
return dp[index][currentSum];
// Include current element
int include = recursive(arr, index + 1, currentSum + arr[index], totalSum, dp);
// Exclude current element
int exclude = recursive(arr, index + 1, currentSum, totalSum, dp);
// Store and return the minimum of both choices
return dp[index][currentSum] = min(include, exclude);
}
int minDifference(vector<int>& arr, int n) {
int totalSum = accumulate(arr.begin(), arr.end(), 0);
// Create DP table initialized to -1
vector<vector<int>> dp(n + 1, vector<int>(totalSum + 1, -1));
return recursive(arr, 0, 0, totalSum, dp);
}
};
Complexity Analysis:
- Time Complexity:
- The recursion tree has
O(n * totalSum)nodes (wherenis the number of elements andtotalSumis the sum of all elements). Each node is visited once and the result is stored, so the time complexity becomes O(n * totalSum).
- The recursion tree has
- Space Complexity:
- The space complexity is dominated by the memoization table (
dp), which has a size ofO(n * totalSum). Additionally, the recursion stack has a depth ofO(n). Thus, the overall space complexity is O(n * totalSum).
- The space complexity is dominated by the memoization table (
3️⃣ Tabulation (Bottom-up Approach)
Intuition:
- Let the total sum of all elements be
S. Since
S1 + S2 = S, minimizing|S1 - S2|becomes:|S1 - (S - S1)| = |2 * S1 - S|So we are trying to find a subset
S1such that2*S1is as close possible toS.
The goal is to pick some elements whose sum is al close as possible to half of the total sum.
Because once we fix one subset, the second is implicitly defined.
The best balance between two subsets happens when the difference between their sums is the smallest, ideally 0.
Approach:
- Calculate the total sum
S. - Use DP to find all possible subset sums up to
S/2. - Pick the one
S1with maximum value such thatdp[S1] == true. - Answer is
S - 2*S1.
Code:
class Solution {
public:
int minDifference(vector<int>& arr, int n) {
int totalSum = accumulate(arr.begin(), arr.end(), 0);
int half = totalSum / 2;
// dp[i][j] = true if subset of first i elements has sum j
vector<vector<bool>> dp(n + 1, vector<bool>(half + 1, false));
// Initialize: sum 0 is always possible with 0 elements
for (int i = 0; i <= n; ++i)
dp[i][0] = true;
// Fill the dp table
for (int i = 1; i <= n; ++i) {
for (int j = 1; j <= half; ++j) {
if (arr[i - 1] <= j) {
// Include or exclude the current element
dp[i][j] = dp[i - 1][j] || dp[i - 1][j - arr[i - 1]];
} else {
// Can't include current element
dp[i][j] = dp[i - 1][j];
}
}
}
// Find the largest j <= totalSum/2 that is reachable
int s1 = 0;
for (int j = half; j >= 0; --j) {
if (dp[n][j]) {
s1 = j;
break;
}
}
return totalSum - 2 * s1;
}
};Complexity Analysis:
- Time Complexity:
O(n * sum) - Space Complexity:
O(n * sum)
