Understanding Binary Search

05 Feb, 2025

Binary Search is an efficient search algorithm used to find an element in a sorted array or solve problems by repeatedly dividing the search space in half. It operates in O(log n) time, making it much faster than linear search algorithms for large datasets.

Note: It only works on the sorted array.

Intuition Behind Binary Search

Binary Search works on the "divide and conquer" strategy, continuously narrowing the search range until the target is found or the search space is exhausted. The key requirement is that the array or range must be sorted. It begins by checking the middle element:

If the middle element is equal to the target, the search is over.
If the target is smaller than the middle element, the search continues in the left half of the array.
If the target is larger, the search continues in the right half.

Tips and Tricks for Binary Search

1️⃣ Midpoint Calculation

Traditionally we calculate the mid point using:

int mid = (left + right) / 2;

However it can cause integer overflow, if both left and right are large, close to the maximum integer value.

To prevent this overflow, you can use the alternative formula:

Always calculate the midpoint using:

int mid = left + (right - left) / 2;

This prevents overflow that might occur when left and right are large.

Example:

Imagine left and right are both near INT_MAX, say:

left = INT_MAX - 2
right = INT_MAX

calculating mid:
    right - left = (INT_MAX) - (INT_MAX - 2) = 2
    (right - left) / 2 = 2 / 2 = 1
    mid = left + 1
        = (INT_MAX - 2) + 1
        = INT_MAX - 1

There is another expression, an alternative way to calculate the middle index by using a bitwise right shift operator (>>) instead of division by 2. This approach is based on the fact that shifting right by one is equivalent to dividing by 2 in integer arithmetic.

int mid = (left + high) >> 1

Performance: Bitwise operations like >> can be marginally faster than division. However, modern compilers typically optimize the division by 2 in mid = (left + right) / 2, so the performance difference is usually negligible.
Overflow Risk: This expression does not prevent overflow when calculating index, as it directly adds left and right.
- If left and right are large values close to the maximum integer limit, adding them will still cause overflow. For example, if left = INT_MAX - 2 and right = INT_MAX, left + right would exceed INT_MAX.

So always use:

mid = left + (right - left) / 2

2️⃣ Edge Cases:

Empty array (arr.size() == 0)
Array with one element
All elements are greater or smaller than the target
Duplicate elements (binary search often requires handling first or last occurrence)

3️⃣ Loop Termination:

The condition for continuing the loop should be left <= right and not left < right. This ensures that every possible element is checked.

while (left <= right) // This ensures that there is atleast one element in search space

Why to use Binary Search ❔

Binary search is a divide-and-conquer algorithm. This means that it works by recursively dividing the search space in half until the desired value is found.

The time complexity of binary search is O(log n), where n is the number of elements in the array. This means that the number of comparisons required to find the desired value grows logarithmically as the size of the array grows.

To understand how binary search works, imagine you are looking for a specific word in a dictionary. You could start by opening the dictionary to the middle page and looking for the word there. If the word is on that page, you are done. If the word is not on that page, you can then narrow down your search to either the first half of the dictionary or the second half of the dictionary. You can continue to narrow down your search in this way until you find the word or until you have searched the entire dictionary.

Binary search works in a similar way. It starts by looking at the middle element of
a sorted array. If the element is the value you are looking for, then binary search
terminates. If the element is not the value you are looking for, then binary search
narrows down its search to either the first half or the second half of the array,
depending on whether the value you are looking for is less than or greater than the
middle element. Binary search continues to narrow down its search in this way until
it finds the value you are looking for or until it has searched the entire array.

The main idea behind binary search is that it can reduce the size of the search space by half at each step. This means that the number of steps required to find the value
you are looking for is logarithmic in the size of the array. For example, if the array contains 100 elements, then binary search will only require 7 steps to find the value you are looking for.

In contrast, a linear search would require 100 steps to find the value you are looking for in this case. This is because a linear search would have to look at every element in the array before it could find the value you are looking for.

The reason why binary search is so efficient is because it can take advantage of the fact that the elements in the array are sorted. This allows binary search to quickly narrow down its search space and find the value you are looking for.

Identify Binary Search Problem ❔

1 Monotonic nature of the problem:

Sorted Array: Binary search is often applied to search for an element in a sorted array. Since the array is sorted, you can confidently decide which half to eliminate based on the comparison.
Monotonic Function or Condition: Binary search can also work on problems where the solution space has a monotonic behavior, even if the data itself isn’t a traditional sorted array. This means that as you move in one direction in the solution space, the value of the function either increases or decreases consistently.

2 Constraints of `n ≤ 10^5`:

The constraint on the array size is within reasonable range, it is often less than or equal to 10^5.

3 Question asks to find the the minimum of maximums, maximum of minimums or some minimum / maximum:

What is its Time Complexity ?

Binary Search has a time complexity of O(log n) because it repeatedly divides the search space half at each step.

Process of Binary Search

Initial Search Range: Binary Search starts with the entire range of possible elements. For example, if you are searching in a sorted array of size n, the initial range is [0, n - 1].
Divide in Half: At each step, the middle of the range is chosen as a potential candidate. The algorithm then eliminates half of the remaining elements based on whether the target is smaller or larger than the middle element.
Repeat Until Found or Exhausted: This halving process continues until the search space is reduced to a single element (or is empty if the element is not found).

Halving the Search Space:

In the first step, the algorithm considers n elements.
In the second step, it considers n/2 elements.
In the third step, it considers n/4 elements.
…
After k steps, the search space is reduced to n/2^k elements.

First Step: n, it can also be written as n / 2^0
Second Step: n / 2, it can also be written as n / 2^1
Third Step: n / 4, it can also be written as n / 2^2
...
After k Step: n / 2^k

This process stops when n / 2^k = 1
Thus n = 2^k
Taking the base-2 logarithm of both sides
log2(n) = log(2^k)

We know the property:- log(m^n) = n logm

so, log2(n) = k log2
k = log(n)
Thus the time complexity of binary search is `O(log n)`

Template

/*
Generalized Binary Search:
        0 1 2 3 4 5 6 
arr[] = [1,2,3,5,7,9,12]
        [F,T,T,T,T,T,T]
        [F,F,T,T,T,T,T]
target = 2

LowerBound -> it is the index of the element in the given arr which is greater than or equal to the target
        (element >= target)
        lowerBound(9) = 5
        lowerBound(10) = 6

UpperBound -> it is the index of the element on the given array which is greater than the target
        (element > target)
        upperBound(9) = 6
        upperBound(10) = 6

*/
/*
BinarySearch -> search for the target
    [F,F,F,F,F,F,F,T,F]

LowerBound:
    [F,F,F,F,F,T,T,T,T,T]

UpperBound
    [F,F,F,T,T,T,T,T]

*/

#include<iostream>
#include<vector>

using namespace std;

// GENERIC TEMPLATE
bool condition(int midVal, int target){
    return midVal >= target;
}

int BinarySearch(vector<int>& arr, int target){

    int n = arr.size();
    int left = 0;
    int right = n-1;

    int ans = -1; // if everything is F, then return initialized value

    while (left <= right){

        int mid = left + (right-left)/2;

        if( condition(arr[mid], target) ){
            ans = mid;
            right = mid-1; // left = mid+1
        }
        else {
            left = mid + 1; // right = mid-1;
        }

    }

    return ans;
}

/*
    NOTES:
    1. left=0 and right=n-1
    2. while(left <= right)
    3. left = mid+1 and right = mid-1  
    4. (left = mid || right = mid) -> not allowed
*/

Patterns

1️⃣ Ad hoc patterns

These are those binary search problems where binary search is applied in unconventional or creative ways to solve problems not explicitly about searching sorted arrays.

Simple Binary Search
First and Last Occurrences in Array
Search Insert Position
Sqrt(x)

2️⃣ Find the Pivot First and then Search

The pivot and then search pattern in binary search is often used in problems where you are dealing with a rotated array.

Find Peak Element
Find in Mountain Array
Single Element in a Sorted Array
Search Element in Rotated Sorted Array (I and II)
Min in a Rotated Sorted Array.

3️⃣ Binary Search on Answers

Normally we use binary search when the given input array is sorted. However, in some problems we have given unsorted input array still we can apply binary search on it. This concept is called as binary search on answers.

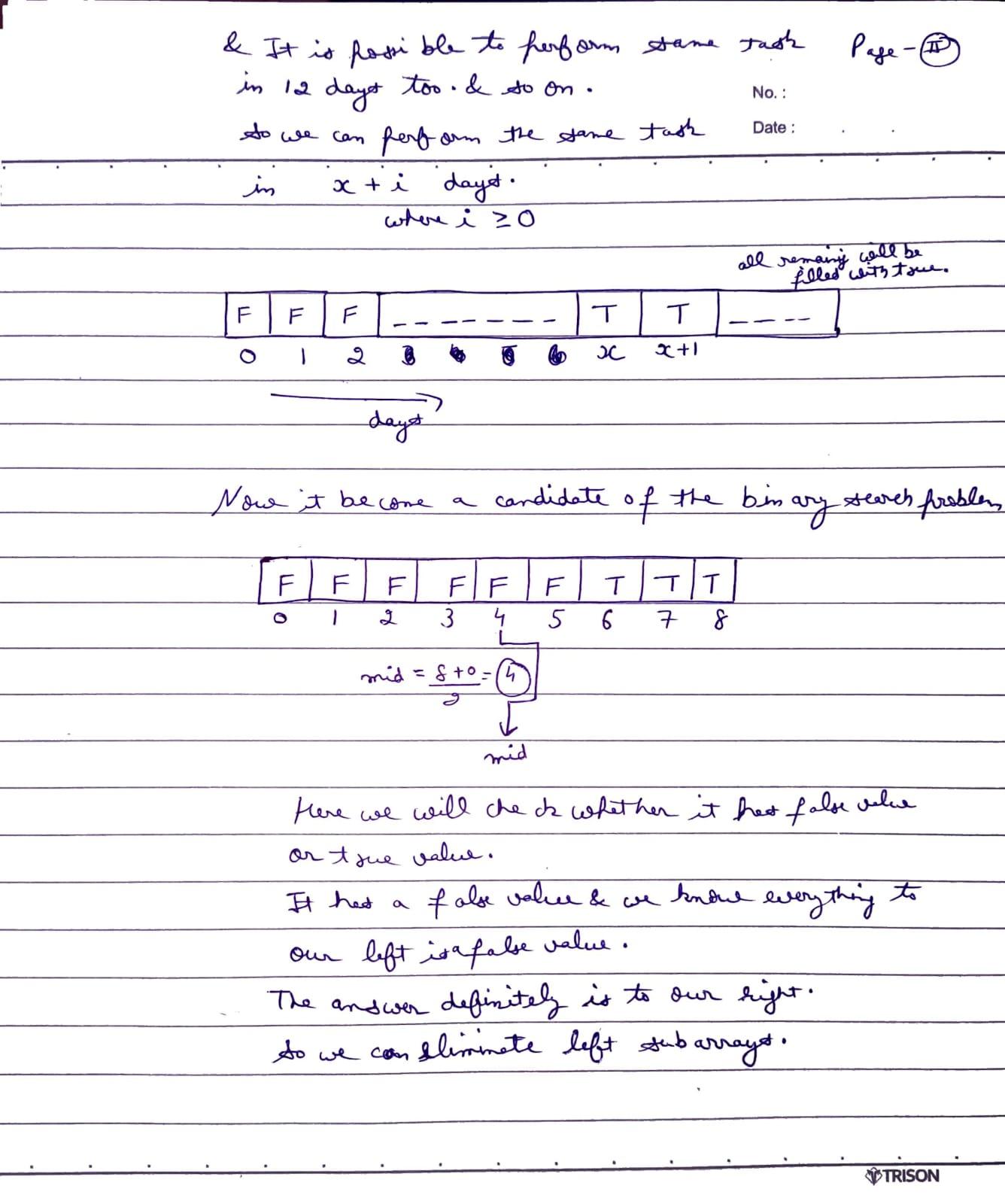
Binary search can be applied on any function that is monotonically increasing or monotonically decreasing. Thus in binary search on an answer such that it will cut the search space in half. This concept generally works on problems that ask to find the maximum or minimum value of some x (which lies in the range from Low to High) for which the predicate function is true. The answer for any x in the search space ([LOW, HIGH]) is decided whether true or false by a function called the Predicate function (Any function which return true or false). It is a boolean function. It returns true if the answer for that x is true and the same for the false. So after each decision, the search space is halved.

It is a technique used in certain types of optimization problems where you need to find the best possible answer from a range of possible solutions. Instead of testing each possible solution sequentially, you apply binary search over the range of possible answers, typically narrowing down the search space by checking if a certain value is feasible or not.

A monotonic predicate function is a function that exhibits a consistent behavior as its input value increases or decreases. Specifically:

Monotonically Increasing Predicate: If the predicate is true for some value x, then it remains true for all value y ≥ x.
Monotonically Decreasing Predicate: If the predicate is true for some value x, then it remains for all values y ≤ x.

There are two types of monotonic predicate functions:

Let's suppose T = true and F = false

Case 1: T T T T F F F - Here we may be asked to find the first false or last true.

We have to find a monotonic function which either return true before any point or false.
T T T T | F F F

Case 2: F F F F T T T - Here we may be asked to find the last false or first true.

According to the question, we have to select the sequence:
predicate_function(low) != predicate_function(high) (The predicate function for extreme ends of the search space needs to be different).

If the predicate is the same for extreme ends then the monotonic sequence looks
like this:
T T T T T T T
F F F F F F F

According to the question. Most of the time, the question asks for a True result:
1. If the question asks for max True in (case: 1), then ans is: low
2. If the question asks for min False in (case: 1), then ans is: high
3. If the question asks for min True in (case: 2), then ans is: high
4. If the question asks for max False in (case: 2), then ans is: low

Tip:

How to identify in these types of problems that its binary search it will be always given to maximize on minimize the answer like finding the largest possible value or least possible value.
And if the answer is monotonous in nature that is its always non-decreasing or always non-increasing.

Intuition:

Template for it:

#include<bits/stdc++.h>
using namespace std;

bool predicate_function(int mid) {

 // if it satisfies the condition then return true
 // else return false
}

int manin() {

 int low, high, mid;

 // Low is the minimum value
 low = Minimum value;
 // High is the maximum value
 high = Maximum value;

 while (high > low + 1) {
  mid = (low + high) / 2;

  if (predicate_function(mid))
   True Part = mid;
  else
   False Part = mid;
 }

 // Ans might be low/high based on the question
 cout << Ans << endl;
}

Problems:

First Bad Version
Koko Eating Bananas
Min days to make M bouquets
Capacity to ship Packages
Aggressive Cows
Painter's Partition Problem
Book Allocation
Splits Array Largest Sum

References for it:

4️⃣ Binary Search on a 2D Array

Search in a 2D Matrix (I & II)
Find the Median in a row-wise sorted matrix

5️⃣ Binary Search on Two Arrays

Median of Two Sorted Arrays
K-th Element of Two Sorted Arrays

STL Functions for it

1️⃣ `std::binary_search`

Determines if a value exists in a sorted range using binary search.

Usage: Return true if the value is found, otherwise returns false.

Complexity: O(log n)

Syntax:

bool binary_search(Iterator first, Iterator last, const T& value);

Example:

#include <iostream>
#include <vector>
#include <algorithm>

int main() {
    std::vector<int> arr = {1, 3, 5, 7, 9, 11};
    bool found = std::binary_search(arr.begin(), arr.end(), 5);
    std::cout << "Found 5: " << (found ? "Yes" : "No") << std::endl;
    return 0;
}

2️⃣ `std::lower_bound≥`

Finds the first element in a sorted range that is not less than (i.e., greater or equal to) a given value.

Usage: Returns an iterator pointing to the first element that is greater than or equal to the target.

Complexity: O(log n)

Syntax:

Iterator lower_bound(Iterator first, Iterator last, const T& value);

first: This is the iterator pointing to the first element of the range.
last: This is the iterator pointing to one position past the last element of the range. This is often referred to as the past-the-end iterator, and it's used to indicate the boundary of the range.

It follows the half-open interval convention: [first, last)

first: The iterator to the first element of the range (inclusive).
last: The iterator to one past the last element of the range (exclusive).
This means:
- The range starts at the element pointed to by first.
- The range ends just before the element pointed to by last.
- The element at last is not included in the range.

Why use `[first, last)` Convention?

Simplicity for Iteration:
- It allows simple without special edge cases.
```
for (auto it = first; it != last; ++it) {
    // Process each element in the range
}
```
- Using [first, last) ensures that the loop terminates naturally when it equals last.
Consistency with STL Algorithms:
1. All STL algorithms, such as std::lower_bound, std::sort, and std::find, use this convention, making it uniform and predictable.
Subranges Are Easy to Specify:
1. With [first, last), it's easy to divide a range into subranges:
  1. Example: If you split [begin, end) into two parts, [begin, mid) and [mid, end), there is no overlap, and the division is clean.
Ease of Handling Empty Ranges:
1. An empty range is naturally represented when first == last.

Example:

#include <iostream>
#include <vector>
#include <algorithm>

int main() {
    std::vector<int> arr = {1, 3, 5, 7, 9, 11};
    auto it = std::lower_bound(arr.begin(), arr.end(), 6);
    std::cout << "Lower bound of 6: " << *it << std::endl;
    return 0;
}

//OR
In

Output:

Lower bound of 6: 7

3️⃣ `std::upper_bound>`

Finds the first element in a sorted range that is greater than the given value.

Usage: Returns a iterator pointing to the first element that is strictly greater than the target.

Complexity: O(log n)

Syntax:

Iterator upper_bound(Iterator first, Iterator last, const T& value);

Example:

#include <iostream>
#include <vector>
#include <algorithm>

int main() {
    std::vector<int> arr = {1, 3, 5, 7, 9, 11};
    auto it = std::upper_bound(arr.begin(), arr.end(), 6);
    std::cout << "Upper bound of 6: " << *it << std::endl;
    return 0;
}

Output:

Upper bound of 6: 7

References:

Templates for Binary Search

These templates are provided by the leetcode, you can check it out here: https://leetcode.com/explore/learn/card/binary-search/

1️⃣ Template 1:

int binarySearch(vector<int>& nums, int target){
  if(nums.size() == 0)
    return -1;

  int left = 0, right = nums.size() - 1;
  while(left <= right){
    // Prevent (left + right) overflow
    int mid = left + (right - left) / 2;
    if(nums[mid] == target){ return mid; }
    else if(nums[mid] < target) { left = mid + 1; }
    else { right = mid - 1; }
  }

  // End Condition: left > right
  return -1;
}

It is the most basic and elementary form of Binary Search.

2️⃣ Template 2:

int binarySearch(vector<int>& nums, int target){
  if(nums.size() == 0)
    return -1;

  int left = 0, right = nums.size() - 1;
  while(left < right){
    // Prevent (left + right) overflow
    int mid = left + (right - left) / 2;
    if(nums[mid] == target){ return mid; }
    else if(nums[mid] < target) { left = mid + 1; }
    else { right = mid; }
  }

  // Post-processing:
  // End Condition: left == right
  if(nums[left] == target) return left;
  return -1;
}

It is an advanced form of Binary Search.

3️⃣ Template 3:

int binarySearch(vector<int>& nums, int target){
    if (nums.size() == 0)
        return -1;

    int left = 0, right = nums.size() - 1;
    while (left + 1 < right){
        // Prevent (left + right) overflow
        int mid = left + (right - left) / 2;
        if (nums[mid] == target) {
            return mid;
        } else if (nums[mid] < target) {
            left = mid;
        } else {
            right = mid;
        }
    }

    // Post-processing:
    // End Condition: left + 1 == right
    if(nums[left] == target) return left;
    if(nums[right] == target) return right;
    return -1;
}

Intuition Behind Binary Search

Tips and Tricks for Binary Search

1️⃣ Midpoint Calculation

Example:

2️⃣ Edge Cases:

3️⃣ Loop Termination:

Why to use Binary Search ❔

Identify Binary Search Problem ❔

1 Monotonic nature of the problem:

2 Constraints of n ≤ 10^5:

3 Question asks to find the the minimum of maximums, maximum of minimums or some minimum / maximum:

What is its Time Complexity ?

Process of Binary Search

Template

Patterns

1️⃣ Ad hoc patterns

2️⃣ Find the Pivot First and then Search

3️⃣ Binary Search on Answers

4️⃣ Binary Search on a 2D Array

5️⃣ Binary Search on Two Arrays

STL Functions for it

1️⃣ std::binary_search

Syntax:

Example:

2️⃣ std::lower_bound≥

Syntax:

Why use [first, last) Convention?

Example:

Output:

3️⃣ std::upper_bound>

Syntax:

Example:

Output:

References:

Templates for Binary Search

1️⃣ Template 1:

2️⃣ Template 2:

3️⃣ Template 3:

AIR POLLUTION

Guess the Output of C++ Program Part 1

Listen to any radio station from any country in your phone.

2 Constraints of `n ≤ 10^5`:

1️⃣ `std::binary_search`

2️⃣ `std::lower_bound≥`

Why use `[first, last)` Convention?

3️⃣ `std::upper_bound>`