Problem Statement
A ninja has planned a n-day training schedule. Each day he has to perform one of three activities - running, stealth training, or fighting practice. The same activity cannot be done on two consecutive days and the ninja earns a specific number of merit points, based on the activity and the given day.
Given a n x 3-sized matrix, where matrix[i][0], matrix[i][1], and matrix[i][2], represent the merit points associated with running, stealth and fighting practice, on the (i+1)th day respectively. Return the maximum possible merit points that the ninja can earn.
Examples
Example 1:
Input: matrix = [[10, 40, 70], [20, 50, 80], [30, 60, 90]]
Output: 210
Explanation:
Day 1: fighting practice = 70
Day 2: stealth training = 50
Day 3: fighting practice = 90
Total = 70 + 50 + 90 = 210
This gives the optimal points.Example 2:
Input: matrix = [[70, 40, 10], [180, 20, 5], [200, 60, 30]]
Output: 290
Explanation:
Day 1: running = 70
Day 2: stealth training = 20
Day 3: running = 200
Total = 70 + 20 + 200 = 290
This gives the optimal points.Different Approaches
Why greedy approach will not work:
As the question asks to maximizing points, the initial approach that comes to mind is the greedy approach. The greedy strategy involves selecting the task with the maximum points each day, ensuring that the same task isn't repeated from the previous day. However, following this approach consistently may result in missing out on tasks that offer higher total points over time.
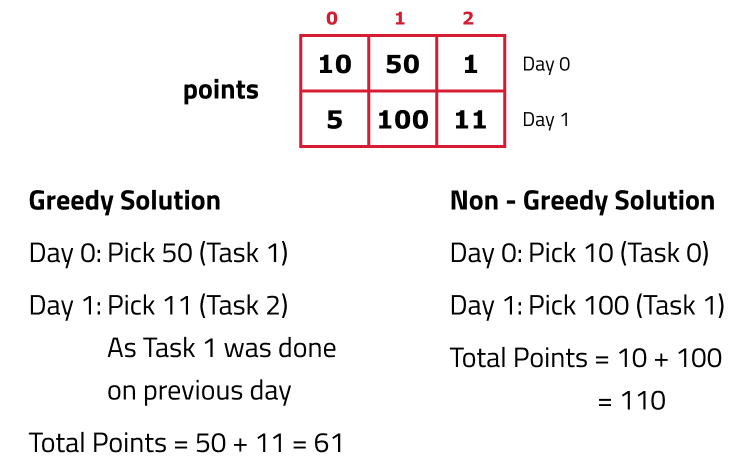
So, we observe that the greedy solution imposes restrictions on our choices, we can lose activity with better points on the next day in the greedy solution. Therefore, it is more advantageous to explore all possible choices as our next solution. We will employ recursion to generate all possible options.
1️⃣ Recursive Approach
Steps to form the recursive solution:
- Express the problem in terms of indexes: On observation we find that the number of days(day0, day1 etc) breaks the problem in different steps. Clearly, we have n days (from 0 to n-1), so one changing parameter which can be expressed in terms of indexes is ‘day’.
Every day we have the option of three activities(say 0,1,2) to be performed. Suppose that we are at a day_i. So we must know the task that was performed on the last day so that we do not repeat it on the present day. It is the ‘last’ choice that we tried out on day_i+1 ( i+1 in case of top-down recursion). Unless we know the last choice we made, we can not decide whether a choice we are making is correct or not.
Now there are three options each day(say 0,1,2) which becomes the ‘last’ of the next day. If we are just starting from the day(n-1), then for this day we can try all three options. We can say ‘last’ for this day is 3, which means any activity can be performed.
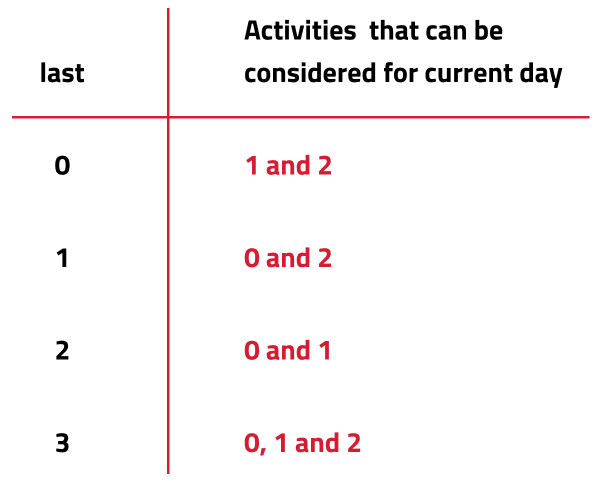
Therefore our function will take two parameters - day and last. f(day, last) will give the maximum points that can be made from day 'day' to day '0', keeping in check that the last activity is not being repeated on consecutive days.
- Try out all possible choices at a given index: We are writing a top-down recursive function. We start from day_n-1 to day_0. Therefore whenever we call the recursive function for the next day we call it for f(day-1, last). Now let’s discuss the second parameter. The choices we have for a current day depend on the ‘last’ variable. If we are at our base case (day=0), we will have the following choices.
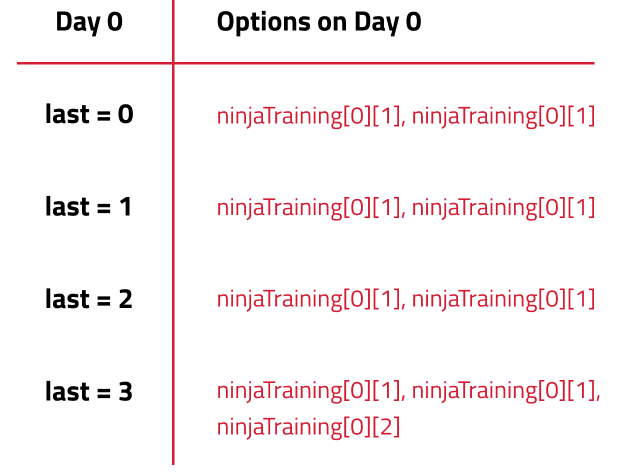
Other than the base case, whenever we perform an activity(i), its merit points will be given by points[day][i] and to get merit points of the remaining days we will let recursion do its job by passing f(d-1, i). We are passing the second parameter as i because the current day’s activity will become the next day’s last.
/*It is pseudocode and it is not tied to
any specific programming language.*/
f(day,last){
if(day == 0){
for(int i = 0; i <= 2; i++){
if(i != last) //code
}
}
for(int i = 0; i <= 2; i++){
if(i != last){
activity = points[day][i] + f(day-1, i)
}
}
}
- Take the maximum of all choices: As the problem statement wants us to find the maximum merit points, take the maximum of all choices.
/*It is pseudocode and it is not tied to
any specific programming language.*/
f(day,last){
if(day == 0){
maxi = 0
for(int i = 0; i <= 2; i++){
if(i != last) maxi = max(maxi,points[0][i]
}
return maxi
}
maxi = 0
for(int i = 0; i <= 2; i++){
if(i != last){
activity = points[day][i] + f(day-1, i)
maxi = max(maxi, activity)
}
}
return maxi
}
- Base condition: when the day is 0, preform the activities according to the 'last' and return the maximum points.
Code:
#include <bits/stdc++.h>
using namespace std;
class Solution {
private:
/* Recursive function to calculate the
maximum points for the ninja training*/
int func(int day, int last, vector<vector<int>> &points) {
// Base case
if (day == 0) {
int maxi = 0;
/* Calculate the maximum points for the first day
by choosing an activity different from last one*/
for (int i = 0; i <= 2; i++) {
if (i != last) maxi = max(maxi, points[0][i]);
}
// Return the maximum points
return maxi;
}
int maxi = 0;
// Iterate through activities for the current day
for (int i = 0; i <= 2; i++) {
if (i != last) {
/* Calculate the points for the current activity
and add it to the maximum points obtained so far */
int activity = points[day][i] + func(day - 1, i, points);
maxi = max(maxi, activity);
}
}
// Return the maximum points
return maxi;
}
public:
int ninjaTraining(vector<vector<int>>& matrix) {
int day = matrix.size()-1;
int last = 3; // any invalid day.
return func(day, last, matrix);
}
};
int main() {
vector<vector<int>> points = {{10, 40, 70},
{20, 50, 80},
{30, 60, 90}};
//Create an instance of Solution class
Solution sol;
cout << sol.ninjaTraining(points);
}Complexity Analysis:
- Time Complexity:
O(3^N), whereNis the given size of 2D array. Exponential time complexity due to the recursive nature where each day can have up to 3 choices. - Space Complexity:
O(N), As the recursion depth is equal to the number of days (days). Therefore, the maximum depth of the recursion stack is O(N).
2️⃣ Memoization
If we draw the recursion tree, we will see that there are overlapping subproblems. Hence DP approaches can be applied on the recursive solution.
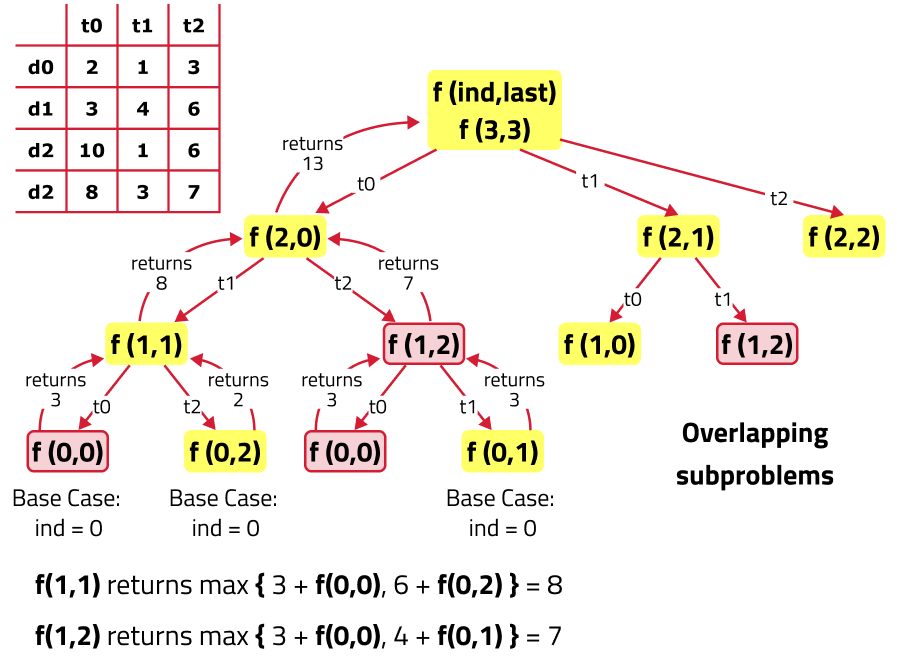

In order to convert a recursive solution to memoization the following steps will be taken:
- Declare a dp array of size [n][4]: As there are two parameters in the recursive solution which are changing, first one is 'day' and the other one is 'last'. There are total ‘n’ days and for every day, there can be 4 choices (0,1,2 and 3). 3 is for no task at all. Therefore we take the dp array as dp[n][4].
It represents the solution to the subproblem for any given index. Initially, fill the array with -1, to indicate that no subproblem has been solved yet.
- While encountering an overlapping subproblem: When we come across a subproblem, for which the dp array has value other than -1, it means we have found a subproblem which has been solved before hence it is an overlapping subproblem. No need to calculate it's value again just retrieve the value from dp array and return it.
- Store the value of subproblem: Whenever, a subproblem is encountered and it is not solved yet(the value at this index will be -1 in the dp array), store the calculated value of subproblem in the array.
Code:
#include <bits/stdc++.h>
using namespace std;
class Solution {
private:
/* Recursive function to calculate the
maximum points for the ninja training*/
int func(int day, int last, vector<vector<int>> &points, vector<vector<int>> &dp) {
/* If the result for this day and last
activity is already calculated, return it*/
if (dp[day][last] != -1) return dp[day][last];
// Base case
if (day == 0) {
int maxi = 0;
/* Calculate the maximum points for the first day
by choosing an activity different from last one*/
for (int i = 0; i <= 2; i++) {
if (i != last) maxi = max(maxi, points[0][i]);
}
// Store the result in dp array and return it
return dp[day][last] = maxi;
}
int maxi = 0;
// Iterate through activities for the current day
for (int i = 0; i <= 2; i++) {
if (i != last) {
/* Calculate the points for the current activity
and add it to the maximum points obtained so far */
int activity = points[day][i] + func(day - 1, i, points, dp);
maxi = max(maxi, activity);
}
}
// Store the result in dp array and return it
return dp[day][last] = maxi;
}
public:
int ninjaTraining(vector<vector<int>>& matrix) {
int day = matrix.size();
/* Create a memoization table
to store intermediate results*/
vector<vector<int>> dp(day, vector<int>(4, -1));
int last = 3;
return func(day-1, last, matrix, dp);
}
};
int main() {
vector<vector<int>> points = {{10, 40, 70},
{20, 50, 80},
{30, 60, 90}};
//Create an instance of Solution class
Solution sol;
cout << sol.ninjaTraining(points);
}Complexity Analysis:
- Time Complexity:
O(N*4*3). There are N*4 states and for every state, we are running a for loop iterating three times. - Space Complexity:
O(N) + O(N*4), We are using a recursion stack space(O(N)) and a 2D array (again O(N*4)). Therefore total space complexity will be O(N) + O(N) ≈ O(N)
3️⃣ Tabulation
In order to convert a recursive code to tabulation code, we try to convert the recursive code to tabulation and here are the steps:
- Declare a dp array of size [n][4]: There are total ‘n’ days and for every day, there can be 4 choices (0,1,2 and 3). Therefore we take the dp array as dp[n][4] and dp[i][j] represents the maximum points at day i, considering the last activity as j.
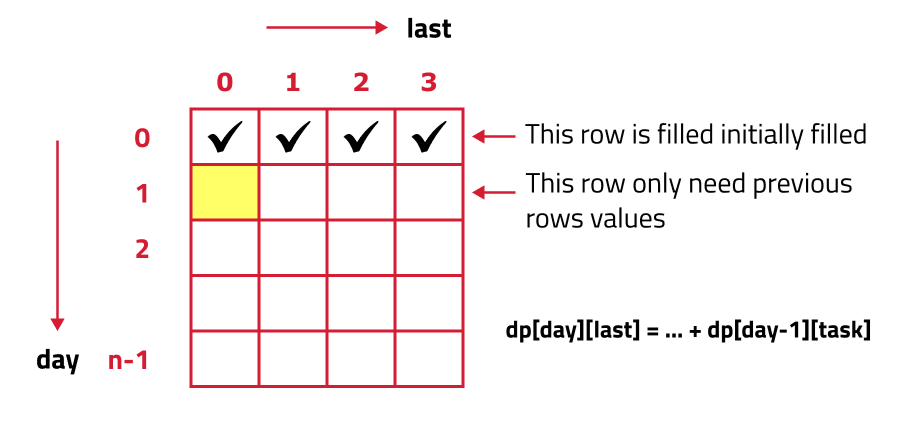
- Setting Base Cases in the Array: In the recursive code, we knew the answer for base case, when 'day' = 0, Therefore, we can say that the following will be the base conditions.
- dp[0][0] = max(points[0][1], points[0][2]), when the last activity is 0.
- dp[0][1] = max(points[0][0], points[0][2]), when the last activity is 1.
- dp[0][2] = max(points[0][0], points[0][1]), when the last activity is 2.
- dp[0][3] = max(points[0][0], points[0][1] and points[0][2]), when the last is 3, it means we are just starting from here and no activity has been performed yet.
- Iterative Computation Using Loops: Set an iterative loop that traverses the array( from index 1 to n-1), for each day iterate through all the 4 choices of the 'last' and then Iterate through the tasks for the current day. Calculate the points for the current activity and add it to the maximum points obtained on the previous day.
- Choosing the maximum: Update dp[day][last] to store the maximum of dp[day][last] and current calculation.
- Returning the last element: The last element of the dp array is returned because it holds the optimal solution to the entire problem after the bottom-up computation has been completed.
Code:
#include <bits/stdc++.h>
using namespace std;
class Solution {
public:
/* Function to calculate the maximum
points for the ninja training*/
int ninjaTraining(vector<vector<int>>& matrix) {
int n = matrix.size();
// Create a 2D DP table to store the maximum points
vector<vector<int>> dp(n, vector<int>(4, 0));
// Initialize the DP table for the first day (day 0)
dp[0][0] = max(matrix[0][1], matrix[0][2]);
dp[0][1] = max(matrix[0][0], matrix[0][2]);
dp[0][2] = max(matrix[0][0], matrix[0][1]);
dp[0][3] = max(matrix[0][0], max(matrix[0][1], matrix[0][2]));
// Iterate through the days starting from day 1
for (int day = 1; day < n; day++) {
for (int last = 0; last < 4; last++) {
dp[day][last] = 0;
// Iterate through the tasks for the current day
for (int task = 0; task <= 2; task++) {
if (task != last) {
/* Calculate the points for the current
activity and add it to the maximum points
obtained on the previous day */
int activity = matrix[day][task] + dp[day - 1][task];
/* Update the maximum points for
the current day and last activity*/
dp[day][last] = max(dp[day][last], activity);
}
}
}
}
/* The maximum points for the last day with
any activity can be found in dp[n-1][3]*/
return dp[n - 1][3];
}
};
int main() {
vector<vector<int>> points = {{10, 40, 70},
{20, 50, 80},
{30, 60, 90}};
//Create an instance of Solution class
Solution sol;
cout << sol.ninjaTraining(points);
}Complexity Analysis:
- Time Complexity:
O(N*4*3). There areN*4states and for every state, we are running a for loop iterating three times. - Space Complexity:
O(N*4), 2D array is being used to store the intermediate calculations.
4️⃣ Space Optimization
If we closely look the relation obtained in the tabulation approach, dp[day][last] = max(dp[day][last],matrix[day][task] + dp[day-1][task])
Here the task can be anything from 0 to 3 and day-1 is the previous stage of recursion. So in order to compute any dp array value, we only require the last row to calculate it.
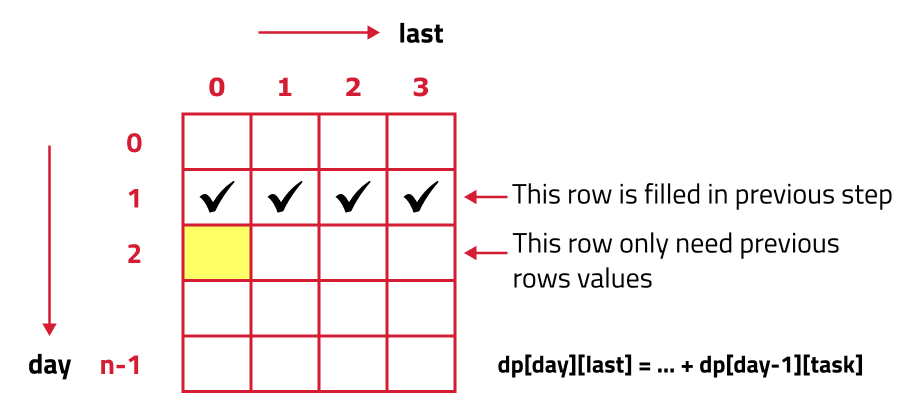
- So rather than storing the entire 2D Array of size N*4, we can just store values of size 4(say prev).
- We can then take a dummy array, again of size 4 (say temp) and calculate the next row’s value using the array we stored in step 1.
- After that whenever we move to the next day, the temp array becomes our prev for the next step.
- At last prev[3] will give us the answer because it will be the last element, storing the maximum points in bottom-up manner.
Code:
#include <bits/stdc++.h>
using namespace std;
class Solution {
public:
/* Function to calculate the maximum
points for the ninja training*/
int ninjaTraining(vector<vector<int>>& matrix) {
int n = matrix.size();
/* Initialize a vector to store the maximum
points for the previous day's activities*/
vector<int> prev(4, 0);
// Initialize the prev array for the first day (day 0)
prev[0] = max(matrix[0][1], matrix[0][2]);
prev[1] = max(matrix[0][0], matrix[0][2]);
prev[2] = max(matrix[0][0], matrix[0][1]);
prev[3] = max(matrix[0][0], max(matrix[0][1], matrix[0][2]));
// Iterate through the days starting from day 1
for (int day = 1; day < n; day++) {
/* Create a temporary vector to store the
maximum points for the current day's activities*/
vector<int> temp(4, 0);
for (int last = 0; last < 4; last++) {
temp[last] = 0;
// Iterate through the tasks for the current day
for (int task = 0; task <= 2; task++) {
if (task != last) {
/* Calculate the points for the current activity
and add it to the maximum points obtained on the
previous day (stored in prev)*/
temp[last] = max(temp[last], matrix[day][task] + prev[task]);
}
}
}
// Update prev with maximum points for the current day
prev = temp;
}
/* The maximum points for the last day with
any activity can be found in prev[3]*/
return prev[3];
}
};
int main() {
vector<vector<int>> points = {{10, 40, 70},
{20, 50, 80},
{30, 60, 90}};
//Create an instance of Solution class
Solution sol;
cout << sol.ninjaTraining(points);
}Complexity Analysis:
- Time Complexity:
O(N*4*3)- There are
N*4states and for every state, we are running a for loop iterating three times.
- There are
- Space Complexity:
O(4), We are using an external array of size ‘4’ to store only one row.
