Problem Statement

Given a 2d integer array named triangle with n rows. Its first row has 1 element and each succeeding row has one more element in it than the row above it. Return the minimum falling path sum from the first row to the last.

Movement is allowed only to the bottom or bottom-right cell from the current cell.

More formally, if you are on index i on the current row, you may move to either index i or index i + 1 on the next row.

Examples

Example 1:

Input: triangle = [[2],[3,4],[6,5,7],[4,1,8,3]]
Output: 11
Explanation: The triangle looks like:
2
3 4
6 5 7
4 1 8 3
The minimum path sum from top to bottom is 2 + 3 + 5 + 1 = 11.

Example 2:

Input: triangle = [[1], [1, 2], [1, 2, 4]]
Output: 3

Explanation: One possible route can be:
Start at 1st row -> bottom -> bottom.

Example 3:

Input: triangle = [[1], [4, 7], [4,10, 50], [-50, 5, 6, -100]]
Output: -42

Explanation: One possible route can be:
Start at 1st row -> bottom-right -> bottom-right -> bottom-right.

Different Approaches

1️⃣ Recursive Approach

Why Greedy Approach will not work:

As the question asks for minimum path sum, the first approach that comes to our mind is to take a greedy approach and always form a path by locally choosing the cheaper option. At every cell, we have two choices, to move to the bottom cell or move to the bottom-right cell. Our ultimate aim is to provide a path that provides us the least path sum. Therefore at every cell, we will make the choice to move which costs us less.

We can clearly see the issue with the greedy solution. When we make local choices, we might select a path that ends up costing us much more later on.

Therefore, the only alternative left to us is to generate all possible paths and determine which path has the minimum path sum. To generate all paths, we will use recursion.

Steps to form the recursive solution:

• Express the problem in terms of indexes: We are given a triangular matrix with the number of rows equal to N. We can define the function with two parameters i and j, where i and j represent the row and column of the matrix.

Now, our ultimate aim is to reach the last row. We can define f(i,j) such that it gives us the minimum path sum from the cell [i][j] to the last row.

• Try out all possible choices at a given index: At every index there are two choices, one to go to the bottom cell(↓) other to the bottom-right cell(↘). To go to the bottom, increase i by 1, and to move towards the bottom-right, increase both i and j by 1.

Now when we get our answer for the recursive call (f(i+1,j) or f(i+1,j+1)), the current cell value also needs to be added to it as we have to include it too for the current path sum

/*It is pseudocode  and it is not tied to 
any specific programming  language*/

f(i,j){
    // Base case here
    
    down =  mat[i][j] + f(i+1, j)
    diagonal = mat[i][j] + f(i+1, j+1)
}

• Take the minimum of all choices: As question asks to find the minimum path sum of all the possible unique paths, return the minimum of the choices(down and diagonal).

/*It is pseudocode  and it is not tied to 
any specific programming  language*/

f(i,j){
    // Base case here
    
    
    down =  mat[i][j] + f(i+1, j)
    diagonal = mat[i][j] + f(i+1, j+1)
    return min(down, diagonal)
}

• Base cases:
  • When i == N-1, that means we have reached the last row, so the minimum path from that cell to the last row will be the value of that cell itself, hence we return mat[i][j].

At every cell, we have two options to move to the bottom cell(↓) or to the bottom-right cell(↘). If we closely observe the triangular grid, at max we can reach the last row from where we return so we will not move out of the index of the grid. Therefore only one base condition is required.

/*It is pseudocode  and it is not tied to 
any specific programming  language*/

f(i,j){
    if(i == N-1)   return mat[i][j]
    
    //code
}

Code:

#include <bits/stdc++.h>
using namespace std;

class Solution {
private:
    /**
     * Recursive function to calculate the minimum path sum
     * for a given cell in the triangle.
     *
     * @param row: Current row index.
     * @param col: Current column index.
     * @param triangle: The input triangle represented as a vector of vectors.
     * @param numRows: Total number of rows in the triangle.
     * @return The minimum path sum starting from (row, col).
     */
    int calculateMinPath(int row, int col, vector<vector<int>> &triangle, int numRows) {
        // Base condition: If we're at the last row, return the value of the current cell
        if (row == numRows - 1)
            return triangle[row][col];
        
        // Recursive calls to calculate the minimum path sum for two possible paths:
        // 1. Downward path (next row, same column)
        int down = triangle[row][col] + calculateMinPath(row + 1, col, triangle, numRows);
        // 2. Diagonal path (next row, next column)
        int diagonal = triangle[row][col] + calculateMinPath(row + 1, col + 1, triangle, numRows);
        
        // Return the minimum of the two possible path sums
        return min(down, diagonal);
    }

public:
    /**
     * Function to calculate the minimum path sum from the top to the bottom of the triangle.
     *
     * @param triangle: The input triangle represented as a vector of vectors.
     * @return The minimum path sum.
     */
    int minTriangleSum(vector<vector<int>> &triangle) {
        int numRows = triangle.size(); // Get the number of rows in the triangle
        
        // Start the recursive calculation from the top of the triangle (row 0, column 0)
        return calculateMinPath(0, 0, triangle, numRows);
    }
};

int main() {
    // Input triangle
    vector<vector<int>> triangle{
        {1},
        {2, 3},
        {3, 6, 7},
        {8, 9, 6, 10}
    };
    
    // Create an instance of the Solution class
    Solution sol;
    
    // Call the minTriangleSum function and print the result
    cout << "Minimum Path Sum: " << sol.minTriangleSum(triangle) << endl;

    return 0;
}

Complexity Analysis:

• Time Complexity: O(2^N), where N is the number of rows. As, each cell has 2 choices and at max the number of subproblems can be N.
• Space Complexity: O(N), The depth of the recursion is proportional to the height of the triangle N. Therefore, the space used by the call stack is O(N).

2️⃣ Memoization

If we draw the recursion tree, we will see that there are overlapping subproblems. Hence the DP approaches can be applied to the recursive solution.

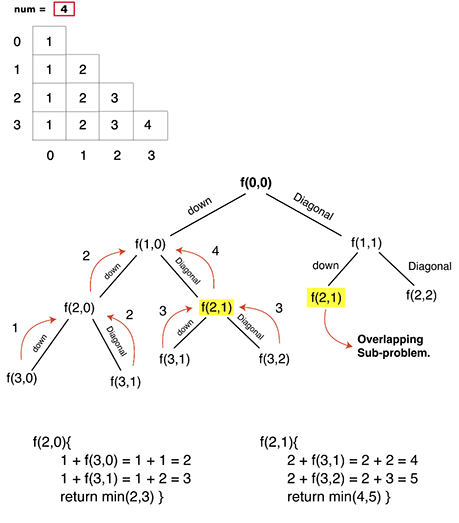
In order to convert a recursive solution to memoization the following steps will be taken:

• Declare a dp[] array of size [n][n]: As there are two changing parameters(i and j) in the recursive solution, and the maximum value they can attain is (n-1) and (n-1), where n is number of rows. So we will require a dp matrix of n*n.
  • The dp array stores the calculations of subproblems, dp[i][j] represents the minimum path sum to reach last row from (i,j). Initially, fill the array with -1, to indicate that no subproblem has been solved yet.
• While encountering an overlapping subproblem: When we come across a subproblem, for which the dp array has value other than -1, it means we have found a subproblem which has been solved before hence it is an overlapping subproblem. No need to calculate it's value again just retrieve the value from dp array and return it.
• Store the value of subproblem: Whenever, a subproblem is enocountered and it is not solved yet(the value at this index will be -1 in the dp array), store the calculated value of subproblem in the array.

Code:

#include <bits/stdc++.h>
using namespace std;

class Solution {
private:
    /**
     * Recursive function to calculate the minimum path sum for a given cell using memoization.
     *
     * @param row: Current row index.
     * @param col: Current column index.
     * @param triangle: The input triangle represented as a vector of vectors.
     * @param numRows: Total number of rows in the triangle.
     * @param memo: Memoization table to store computed results.
     * @return The minimum path sum starting from (row, col).
     */
    int calculateMinPath(int row, int col, vector<vector<int>> &triangle, int numRows, vector<vector<int>> &memo) {
        // If the result for the current cell is already computed, return it from the memo table
        if (memo[row][col] != -1)
            return memo[row][col];
        
        // Base condition: If we're at the last row, return the value of the current cell
        if (row == numRows - 1)
            return triangle[row][col];
        
        // Recursive calls to calculate the minimum path sum for two possible paths:
        // 1. Downward path (next row, same column)
        int downPath = triangle[row][col] + calculateMinPath(row + 1, col, triangle, numRows, memo);
        // 2. Diagonal path (next row, next column)
        int diagonalPath = triangle[row][col] + calculateMinPath(row + 1, col + 1, triangle, numRows, memo);
        
        // Store the minimum path sum for the current cell in the memo table and return it
        return memo[row][col] = min(downPath, diagonalPath);
    }

public:
    /**
     * Function to calculate the minimum path sum from the top to the bottom of the triangle.
     *
     * @param triangle: The input triangle represented as a vector of vectors.
     * @return The minimum path sum.
     */
    int minTriangleSum(vector<vector<int>> &triangle) {
        int numRows = triangle.size(); // Get the number of rows in the triangle
        
        // Initialize a memoization table with -1 to store intermediate results
        vector<vector<int>> memo(numRows, vector<int>(numRows, -1));
        
        // Start the recursive calculation from the top of the triangle (row 0, column 0)
        return calculateMinPath(0, 0, triangle, numRows, memo);
    }
};

int main() {
    // Input triangle
    vector<vector<int>> triangle{
        {1},
        {2, 3},
        {3, 6, 7},
        {8, 9, 6, 10}
    };
    
    // Create an instance of the Solution class
    Solution solution;
    
    // Call the minTriangleSum function and print the result
    cout << "Minimum Path Sum: " << solution.minTriangleSum(triangle) << endl;

    return 0;
}

Complexity Analysis:

• Time Complexity: O(N), where N is the number of rows. As the total number of different subproblems can go up to N.
• Space Complexity: O(N) + O(N*N), We are using a recursion stack space of N and an extra DP array of size N*N.

3️⃣ Tabulation

In order to convert a recursive code to tabulation code, we try to convert the recursive code to tabulation and here are the steps:

• Declare a dp[] array of size [n][n]: As there are two changing parameters(i and j) in the recursive solution, and the maximum value they can attain is (n-1) and (n-1), where n is number of rows. So we will require a dp matrix of n*n. The dp array stores the calculations of subproblems, dp[i][j] represents the minimum path sum to reach (0,0) from (i,j).
• Setting Base Cases in the Array: In the recursive code, we knew that, when i = n-1, it means we have reached the last row and the minimum path to reach the last row from here is the cell value itself. So fill the last row of the dp matrix to the last row of the triangle matrix, dp[n - 1][j] = triangle[n - 1][j].
• Iterative Computation Using Loops: We can use two nested loops to have this traversal. If we see the memoized code, the values required for dp[i][j] are dp[i+1][j] and dp[i+1][j+1]. So the values from the ‘i+1’ row is required only. The last row (i=N-1) is already filled for the base case, so, now move from row ‘N-2’ row and move upwards to find the values correctly.
• Choosing the minimum: As the question asks for minimum path sum, so update dp[i][j] as the minimum of (down and diagonal).
• Returning the first element: The first element dp[0][0] of the dp array is returned because it holds the optimal solution to the entire problem after the top-down computation has been completed.

Code:

 #include <bits/stdc++.h>
using namespace std;

class Solution {
private:
    // Function to find the minimum path sum using tabulation
    int func(vector<vector<int> > &triangle, int n, vector<vector<int> > &dp) {
        /* Initialize the bottom row of dp 
        with the values from the triangle*/
        for (int j = 0; j < n; j++) {
            dp[n - 1][j] = triangle[n - 1][j];
        }

        // Iterate through the triangle rows in reverse order
        for (int i = n - 2; i >= 0; i--) {
            for (int j = i; j >= 0; j--) {
                // Calculate the minimum path sum for current cell
                int down = triangle[i][j] + dp[i + 1][j];
                int diagonal = triangle[i][j] + dp[i + 1][j + 1];

                // Store the minimum of the two possible paths in dp
                dp[i][j] = min(down, diagonal);
            }
        }
        // Top-left cell of dp now contains the minimum path sum
        return dp[0][0];
    }
public:
    //Function to find out the minimum path sum
    int minTriangleSum(vector<vector<int>>& triangle) {
        // Get the number of rows in the triangle
        int n = triangle.size();
        
        /* Initialize a memoization table
        to store computed results*/
        vector<vector<int> > dp(n, vector<int>(n, -1));
    
        //Return the minimum path sum
        return func(triangle, n, dp);
    }
};
int main() {
    vector<vector<int> > triangle{{1},
                                   {2, 3},
                                   {3, 6, 7},
                                   {8, 9, 6, 10}};
    
    //Create an instance of the Solution class
    Solution sol;
    
    // Call the minimumPathSum function and print result
    cout << sol.minTriangleSum(triangle);

    return 0;
}

Complexity Analysis:

• Time Complexity: O(N*N), where N is the number of rows. As the whole triangle is traversed once using two nested loops.
• Space Complexity: O(N*N), As an external DP Array of size ‘N*N’ is used to store the intermediate calculations.

4️⃣ Space Optimization

If we closely look at the relationship obtained in the tabulation approach, dp[i][j] = dp[i+1][j] + dp[i+1][j+1]), We see that the next row is only needed, in order to calculate dp[i][j]. Therefore space optimization can be applied on tabulation approach.

• Initially we can take a dummy row ( say front). It is initialized to the triangle matrix's last row( as done in tabulation).
• Now the current row(say cur) only needs the front row’s value in order to calculate dp[i][j].
   

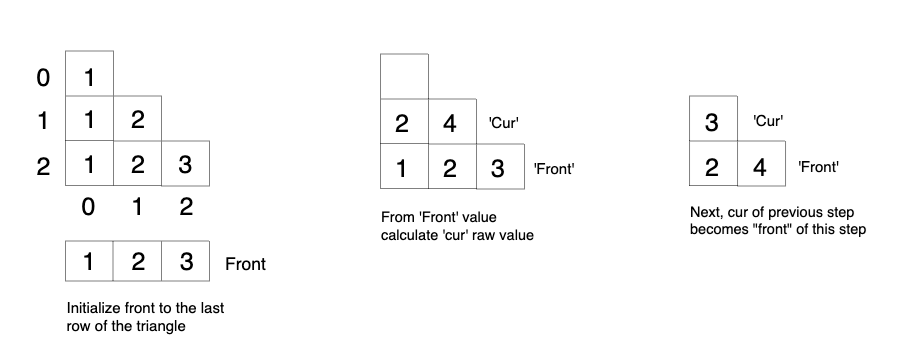
• At the next step, the 'cur' array becomes the 'front' of the next step and using its values we can still calculate the next row’s values.
• At last, front [0] will give us the required answer for bottom-up approach.

Code:

#include <bits/stdc++.h>
using namespace std;

class Solution {
private:
    // Function to find minimum path sum using space optimization
    int func(vector<vector<int> > &triangle, int n) {
        /* Create two arrays to store the
        current and previous row values*/
        
        // Represents the previous row
        vector<int> front(n, 0); 
        
        // Represents the current row
        vector<int> cur(n, 0);   
    
        /* Initialize the front array with values
        from the last row of the triangle*/
        for (int j = 0; j < n; j++) {
            front[j] = triangle[n - 1][j];
        }
    
        // Iterate through triangle rows in reverse order
        for (int i = n - 2; i >= 0; i--) {
            for (int j = i; j >= 0; j--) {
                // Calculate minimum path sum for current cell
                int down = triangle[i][j] + front[j];
                int diagonal = triangle[i][j] + front[j + 1];
            
                /* Store the minimum of the two 
                possible paths in the current row*/
                cur[j] = min(down, diagonal);
            }
            /* Update the front array with
            the values from the current row*/
            front = cur;
        }
    
        /* The front array now contains the minimum path 
        sum from the top to the bottom of the triangle*/
        return front[0];
    }
public:
    //Function to find out the minimum path sum
    int minTriangleSum(vector<vector<int>>& triangle) {
        // Get the number of rows in the triangle
        int n = triangle.size();
    
        //Return the minimum path sum
        return func(triangle, n);
    }
};
int main() {
    vector<vector<int> > triangle{{1},
                                   {2, 3},
                                   {3, 6, 7},
                                   {8, 9, 6, 10}};
    
    //Create an instance of the Solution class
    Solution sol;
    
    // Call the minimumPathSum function and print result
    cout << sol.minTriangleSum(triangle);

    return 0;
}

Complexity Analysis:

• Time Complexity: O(N*N), where N is the number of rows. As the whole triangle is traversed once using two nested loops.
• Space Complexity: O(N)+O(N), As two external array of size ‘N’ is used to store the intermediate calculations of rows.