Problem Statement
A frog wants to climb a staircase with n steps. Given an integer array heights, where heights[i] contains the height of the ith step, and an integer k.
To jump from the ith step to the jth step, the frog requires abs(heights[i] - heights[j]) energy, where abs() denotes the absolute difference. The frog can jump from the ith step to any step in the range [i + 1, i + k], provided it exists. Return the minimum amount of energy required by the frog to go from the 0th step to the (n-1)th step.
Examples
Example 1:
0 1 2 3 4 <- steps
Input: heights = [10, 5, 20, 0, 15], k = 2
Output: 15
Explanation:
Oth step to 2nd step, cost = abs(10 - 20) = 10
2nd step to 4th step, cost = abs(20 - 15) = 5
Total cost = 10 + 5 = 15Example 2:
0 1 2 3 4 <- steps
Input: heights = [15, 4, 1, 14, 15], k = 3
Output: 2
Explanation:
0th step to 3rd step, cost = abs(15 - 14) = 1
3rd step to 4th step, cost = abs(14 - 15) = 1
Total cost = 1 + 1 = 2Different Approaches
1️⃣ Recursion
Intuition:
The problem here is asking for the minimum possible energy and as discussed in the previous problem, this kind of problem can be solved using recursion.
Using the steps described in previous problem, write the recursive solution:
- Express the problem in terms of indexes: This can be easily done as there are array indexes
[0,1,2,..., n-1]. Asf(n-1)signifies the minimum amount of energy required to move from stair0 to stair n-1. Thereforef(0)simply should give us the answer as0(base case). - Try all the choices to reach the goal: As the frog can make jump up to
Ksteps. Therefore, we can set a for loop to run from1 to K, and in each iteration, a function call will be made, corresponding to a step. - Take the minimum of all the choices: As the problem statement asks to find the minimum total energy, return the minimum of all
Kchoices. Also if the index is less than the number of steps, we can’t try the all that step.
/*It is pseudocode and not tied to
any specific programming language.*/
f(ind, height){
if(ind == 0) return 0
mmSteps = INT_MAX
for(int j = 1; j <= K; j++){
if((ind - j) >= 0){
jump = f((ind - j), height) + abs(a[ind] - a[ind-j]);
mmSteps = min(mmSteps, jump);
}
}
return mmSteps;
}- Base case:
- When
n = 0, then we will have only one option to stay at the same place and that would take 0 energy.
- When
Code:
#include <bits/stdc++.h>
using namespace std;
class Solution {
private:
//Helper function for recursion
int func(int ind, vector<int> &heights, int k){
//Base case
if(ind == 0){
return 0;
}
//Initialize mmStep to INT_MAX
int mmStep = INT_MAX;
//Try all possible steps
for(int j = 1; j <= k; j++){
//Check if ind-j is non negative
if(ind-j >= 0){
int jump = func(ind - j, heights, k) + abs(heights[ind] - heights[ind - j]);
//Update the mimimum energy
mmStep = min(jump, mmStep);
}
}
//Return the answer
return mmStep;
}
public:
/* Function to find the mimimum
energy to reach last stair*/
int frogJump(vector<int> &heights, int k) {
int ind = heights.size()-1;
//Return the mimimum energy
return func(ind, heights, k);
}
};
int main() {
vector<int> height{15, 4, 1, 14, 15};
int k = 3;
// Create an instance of Solution class
Solution sol;
// Print the answer
cout << "Minimum energy : " << sol.frogJump(height, k) << endl;
return 0;
}
Complexity Analysis:
- Time Complexity:
O(k ^ n)- The function is called recursively for each index from
n-1down to0, wherenis the length of the heights array. - Total Number of calls:
- At each level of recursion, the number of calls grows by a factor of
k:- At level 0 (base case), there is 1 call.
- At level 1, there are up to
kcalls. - At level 2, there are up to
k^2calls. - ...
- At level
n-1, there are up tok^(n - 1)calls.
- So total number of calls is:
O(k ^ n).
- At each level of recursion, the number of calls grows by a factor of
- The function is called recursively for each index from
- Space Complexity: The space complexity of this recursive approach is
O(n). This is because the maximum depth of the recursion stack can go up to n, due to the linear nature of the stack usage relative to the input sizen.
2️⃣ Memoization
Memoization tends to store the value of subproblems in some map/ table. As, here we have only one parameter in recursive function, so we can create an 1D array to store the values of subproblems.
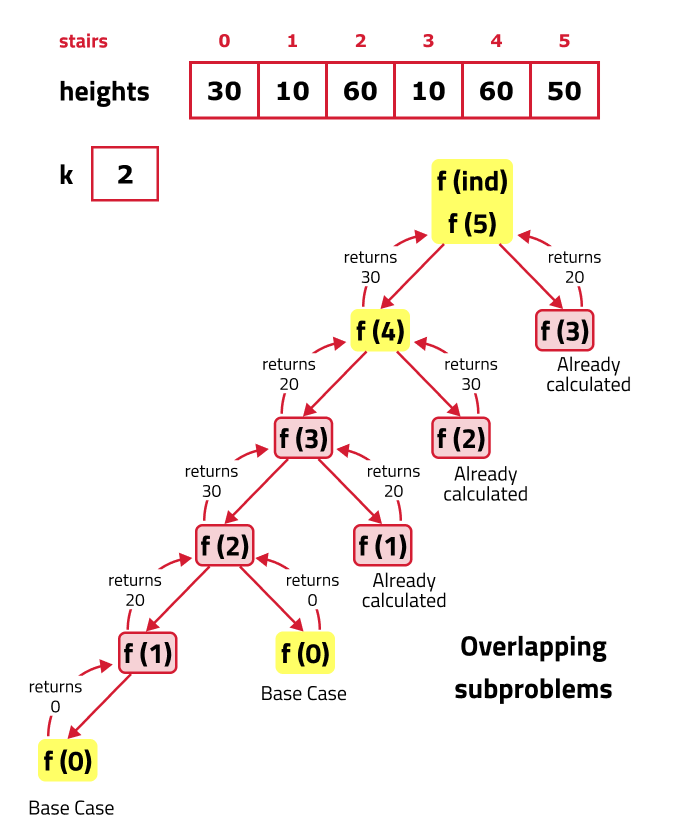
Steps to convert Recursive code to memoization solution:
- Declare an Array dp[] of Size n: Here, n is the parameter or size of the problem, as the highest number of subproblems can be n(including 0 as well). It represents the solution to the subproblem for any given index. Initially, fill the array with -1, to indicate that no subproblem has been solved yet.
- While encountering an overlapping subproblem: When we come across a subproblem, for which the dp array has value other than -1, it means we have found a subproblem which has been solved before hence it is an overlapping subproblem. No need to calculate it's value again just retrieve the value from dp array and return it.
- Store the value of subproblem: Whenever, a subproblem is encountered and it is not solved yet(the value at this index will be -1 in the dp array), store the calculated value of subproblem in the array.
Code:
#include <bits/stdc++.h>
using namespace std;
class Solution {
private:
// Function to recursion with memoization
int func(int ind, vector<int> &heights, int k, vector<int>& dp){
//Base case
if(ind == 0){
return 0;
}
/* If the result for this index has
been previously calculated, return it */
if (dp[ind] != -1) return dp[ind];
//Initialize mmStep to INT_MAX
int mmStep = INT_MAX;
//Try all possible steps
for(int j = 1; j <= k; j++){
//Check if ind-j is non negative
if(ind-j >= 0){
int jump = func(ind-j, heights, k, dp) + abs(heights[ind] - heights[ind-j]);
//Update the mimimum energy
mmStep = min(jump, mmStep);
}
}
//Return the answer
return dp[ind] = mmStep;
}
public:
/* Function to find the mimimum
energy to reach last stair*/
int frogJump(vector<int> &heights, int k) {
int ind = heights.size()-1;
/*Initialize a memoization array
to store calculated results*/
vector<int> dp(ind+1, -1);
//Return the mimimum energy
return func(ind, heights, k, dp);
}
};
int main() {
vector<int> height{15, 4, 1, 14, 15};
int k = 3;
// Create an instance of Solution class
Solution sol;
// Print the answer
cout << "Minimum energy : " << sol.frogJump(height, k) << endl;
return 0;
}Complexity Analysis:
- Time Complexity:
O(k*N),The function is called recursively for each index from N-1 down to 0. For each index, the function explores up to k possible jumps, where N is the length of the heights array. - Space Complexity:
O(N)+O(N), We are using a recursion stack space O(N) and an array (again O(N)). Therefore total space complexity will be O(N) + O(N) ≈ O(N).
3️⃣ Tabulation
In order to convert a recursive code to tabulation code, we try to convert the recursive code to tabulation and here are the steps:
- Bottom-Up Approach in Tabulation: Tabulation involves solving a problem by building a solution from the bottom up. This means start with the smallest subproblems and iteratively compute solutions for larger subproblems until the desired solution has been found.
- Declare an Array dp[] of Size n: Here,
nis the size of the array. It represents the solution to the subproblem for any given index. - Setting Base Cases in the Array: In the recursive code, we knew the answer for base case, when
N = 0, we had only one choice, to stay at0and that takes0energy. Similarly if we are computing in tabulation, we definitely know that the answer fordp[0] = 0. - Iterative Computation Using a Loop: Set an iterative loop that traverses the array( from index
1 to n-1). To compute the solution for larger values, use a loop that iterates from the smallest subproblem up to n. - Explanation of dp[i] Calculation: The current value(dp[i]) represents the subproblem and by the recurrence relation it is obvious that dp[i] is calculated by considering all possible 'k' previous stairs, from where the frog could jump to i.
- Choosing the minimum: Among all the computed energies for each jump(from 1 to k), dp[i] is set to the minimum value. This ensures that dp[i] holds the minimum energy required.
- Returning the last element: The last element of the dp array is returned because it holds the optimal solution to the entire problem after the bottom-up computation has been completed.
Code:
#include <bits/stdc++.h>
using namespace std;
class Solution {
public:
/* Function to find the mimimum
energy to reach last stair*/
int frogJump(vector<int> &heights, int k) {
int ind = heights.size();
/*Initialize a memoization array
to store calculated results*/
vector<int> dp(ind + 1, -1);
dp[0] = 0;
// Loop through the array
for (int i = 1; i < ind; i++) {
int mmSteps = INT_MAX;
// Loop to try all possible jumps from '1' to 'k'
for (int j = 1; j <= k; j++) {
if (i - j >= 0) {
int jump = dp[i - j] + abs(heights[i] - heights[i - j]);
//Update the Minimum energy
mmSteps = min(jump, mmSteps);
}
}
dp[i] = mmSteps;
}
//Result is stored in the last element of dp
return dp[ind - 1];
}
};
int main() {
vector<int> height {15,4,1,14,15};
int k = 3;
// Create an instance of Solution class
Solution sol;
// Print the answer
cout << "Minimum energy : " << sol.frogJump(height, k) << endl;
return 0;
}Complexity Analysis:
- Time Complexity:
O(N*k), whereNis the given size of given array. As for each element of the array, we are considering all possible steps from 1 to k. - Space Complexity:
O(N), an additional array dp of size n is used to store intermediate results. Hence, the space complexity is O(N).
