Problem Statement

Given a m*n binary matrix filled with 0's and 1's, find the largest rectangle containing only 1's and return its area.

Examples

Example 1:

Input: matrix = [
                 [1, 0, 1, 0, 0],
                 [1, 0, 1, 1, 1],
                 [1, 1, 1, 1, 1],
                 [1, 0, 0, 1, 0]
                ]
Output: 6

Explanation: The highlighted part depicts the rectangle with the largest area i.e. 6.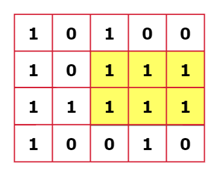

Example 2:

Input: matrix = [[1]]
Output: 1

Explanation: In this case, there is only one rectangle with area 1.

Example 3:

Input: matrix = [
                 [1, 0, 1, 0, 0],
                 [1, 0, 1, 1, 1]
                ]
Output: 3

Different Approaches

1️⃣ Stack

Intuition:

A clever way to approach this problem is by breaking the problem into smaller subproblems using the concept discussed in the problem Largest rectangle in a histogram. The given matrix can be seen from different ground levels. Each ground can be treated as a histogram, and the columns of 1s attached from the ground represent the heights of the bars for the current histogram. This way the problem boils down to finding the largest rectangle in all the histograms.

Now, to find the height of bars for a particular ground level (histogram), traversing the matrix again and again will be inefficient. Instead, the heights of bars can be determined by traversing the matrix only once by using the concept of Prefix Sum.

Understanding:

Since the heights of the bars are the main concern, the prefix sum must be calculated column-wise. This will make sure that while traversing in a column-order fashion, the heights are added up. But if in any place, a zero is found, the height of 1s above it will not be considered as there is no contact of continuous 1s with the ground for that particular histogram.

Approach:

1. Convert the binary matrix into a matrix of histogram heights using the prefix sum technique. Each cell in the histogram matrix represents the height of consecutive 1s ending at that cell.
2. For each column, compute the height of consecutive 1's for each row. If a cell contains a 0, reset the height to 0.
3. For each row in the histogram matrix, treat it as a histogram and compute the largest rectangle area that can be formed using that row. This is achieved using a stack-based approach to find the largest rectangle in a histogram.
4. Track the maximum rectangle area found across all rows and return it as the result.

Code:

class Solution
{
public:
    // Function to find the largest rectangle area in a histogram
    int largestRectangleArea(vector<int> &heights) {

        int n = heights.size();           // Total number of bars in histogram
        stack<int> st;                    // Stack to store indices of bars
        int largestArea = 0;              // To track the maximum area found
        int area;                         // Area of the rectangle at each step
        int nse, pse;                     // Next Smaller Element and Previous Smaller Element indices

        // Traverse all bars in the histogram
        for (int i = 0; i < n; i++) {
            // While current bar is smaller than the top of the stack
            while (!st.empty() && heights[st.top()] >= heights[i]) {
                int ind = st.top();       // Index of the bar being popped
                st.pop();

                // Previous Smaller Element
                pse = st.empty() ? -1 : st.top();

                // Next Smaller Element is current index
                nse = i;

                // Width = nse - pse - 1
                area = heights[ind] * (nse - pse - 1);

                // Update max area if found greater
                largestArea = max(largestArea, area);
            }

            // Push current index to stack
            st.push(i);
        }

        // Process the remaining bars in the stack
        while (!st.empty()) {
            int ind = st.top(); st.pop();

            // Next Smaller Element is end of array
            nse = n;

            // Previous Smaller Element
            pse = st.empty() ? -1 : st.top();

            // Width = nse - pse - 1
            area = heights[ind] * (nse - pse - 1);

            // Update max area if found greater
            largestArea = max(largestArea, area);
        }

        // Return the largest area found
        return largestArea;
    }

    // Function to find the maximal rectangle of all 1s in a binary matrix
    int maximalAreaOfSubMatrixOfAll1(vector<vector<int>> &matrix) {
        int n = matrix.size();         // Number of rows
        int m = matrix[0].size();      // Number of columns

        // Convert the matrix into histogram-style heights
        // Start from the second row and build cumulative column heights
        for (int i = 1; i < n; i++) {
            for (int j = 0; j < m; j++) {
                // If the current cell is 1, add the height from the row above
                if (matrix[i][j] == 1) {
                    matrix[i][j] += matrix[i - 1][j];
                }
            }
        }

        int maxArea = 0;

        // Each row is now a histogram; calculate largest rectangle in each
        for (int i = 0; i < n; i++) {
            maxArea = max(maxArea, largestRectangleArea(matrix[i]));
        }

        // Return the maximum area of all 1s rectangle
        return maxArea;
    }
};

Complexity Analysis:

• Time Complexity:O(N*M) (where N and M are the dimensions of the given matrix)
  • Filling the prefix sum matrix takes O(N*M) time.
  • Every row (of length M) is treated as a histogram for which the largest histogram is found in linear(O(2*M)) time taking overall O(N*M) time.
• Space Complexity:O(N*M)
  • The prefix sum array takes up O(N*M) space.
  • Finding the largest rectangle in each histogram (of length M) takes O(M) space due to stack.