Problem Statement
Given a directed graph with V vertices labeled from 0 to V-1. The graph is represented using an adjacency list where adj[i] lists all nodes adjacent to node i, meaning there is an edge from node i to each node in adj[i]. A node is a terminal node if there are no outgoing edges. A node is a safe node if every possible path starting from that node leads to a terminal node. Return an array containing all the safe nodes of the graph in ascending order.
Examples
Example 1:
Input: V = 7,
adj = [
[1,2],
[2,3],
[5],
[0],
[5],
[],
[]
]
Output: [2, 4, 5, 6]
Explanation:
From node 0: two paths are there 0->2->5 and 0->1->3->0.
The second path does not end at a terminal node. So it is not
a safe node.
From node 1: two paths exist: 1->3->0->1 and 1->2->5.
But the first one does not end at a terminal node. So it is not a safe node.
From node 2: only one path: 2->5 and 5 is a terminal node.
So it is a safe node.
From node 3: two paths: 3->0->1->3 and 3->0->2->5
but the first path does not end at a terminal node.
So it is not a safe node.
From node 4: Only one path: 4->5 and 5 is a terminal node.
So it is also a safe node.
From node 5: It is a terminal node.
So it is a safe node as well.
From node 6: It is a terminal node.
So it is a safe node as well.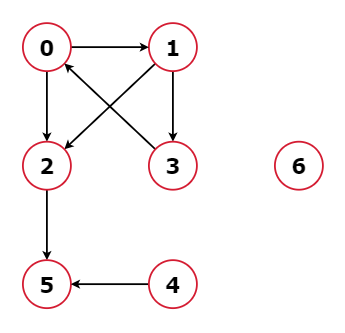
Example 2:
Input: V = 4,
adj =
[
[1],
[2],
[0,3],
[]
]
Output: [3]
Explanation:
Node 3 itself is a terminal node and it is a safe node as well. But all the paths from other nodes do not lead to a terminal node.So they are excluded from the answer.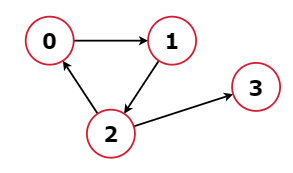
Different Approaches
1️⃣ DFS
Intuition:
It can be observed that all possible paths starting from a node are going to end at some terminal node unless there exists a cycle and the paths return back to themselves.
Understanding:
Consider the below graph:
It is clear that these types of nodes will never be considered safe:
- One is which are occuring in a cycle. Example: Nodes 0, 1 and 3.
- Second is which are leading to a cycle. Example: Node 7.
Except these types of nodes, all other nodes will be considered eventually.
Hence in order to find the safe nodes, the unsafe nodes can be detected by checking if they exist or point to a cycle. Now, a cycle detection technique is already known to us as discussed in detect cycles in a Directed graph (Using DFS).
Approach:
- Color Marking for Nodes:
- Use a visited array where:
- 0: Node is unvisited.
- 1: Node is being visited (part of the current DFS recursion stack).
- 2: Node is safe.
- Use a visited array where:
- Key Idea:
- If a node leads to a cycle, it is not safe.
- If all paths from a node lead to safe nodes, then it is safe.
- DFS Implementation:
- Traverse the graph using DFS.
- Mark the node as 1 (visiting).
- If you visit a node already marked as 1, it’s part of a cycle.
- If all neighbors are safe (2), mark the current node as 2.
Code:
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
class Solution {
public:
bool dfs(int node, vector<vector<int>>& graph, vector<int>& visited) {
if (visited[node] == 1) return false; // Part of a cycle
if (visited[node] == 2) return true; // Already determined as safe
visited[node] = 1; // Mark as visiting
for (int neighbor : graph[node]) {
if (!dfs(neighbor, graph, visited)) {
return false; // If any neighbor is unsafe, this node is unsafe
}
}
visited[node] = 2; // Mark as safe
return true;
}
vector<int> eventualSafeNodes(vector<vector<int>>& graph) {
int n = graph.size();
vector<int> visited(n, 0); // 0 = unvisited, 1 = visiting, 2 = safe
vector<int> safeNodes;
for (int i = 0; i < n; i++) {
if (dfs(i, graph, visited)) {
safeNodes.push_back(i); // Add to safe nodes if DFS confirms safety
}
}
return safeNodes;
}
};
int main() {
Solution sol;
// Example graph: adjacency list representation
vector<vector<int>> graph = {
{1, 2}, // Node 0 -> 1, 2
{2, 3}, // Node 1 -> 2, 3
{5}, // Node 2 -> 5
{0}, // Node 3 -> 0
{5}, // Node 4 -> 5
{}, // Node 5 -> (Terminal node)
};
vector<int> result = sol.eventualSafeNodes(graph);
// Output the result
cout << "Eventual safe nodes: ";
for (int node : result) {
cout << node << " ";
}
cout << endl;
return 0;
}
Complexity Analysis:
- Time Complexity:
O(V+E)(where V and E represents the number of nodes and edges in the given graph)
DFS traversal takes O(V+E) time and adding the safe nodes to the result takes O(V) time. - Space Complexity:
O(V)- The visited array take O(V) space and the recursion stack space will be O(V) in the worst case.
2️⃣ BFS
Intuition:
It can be observed that all possible paths starting from a node are going to end at some terminal node unless there exists a cycle and the paths return back to themselves.
Understanding:
Consider the below graph:
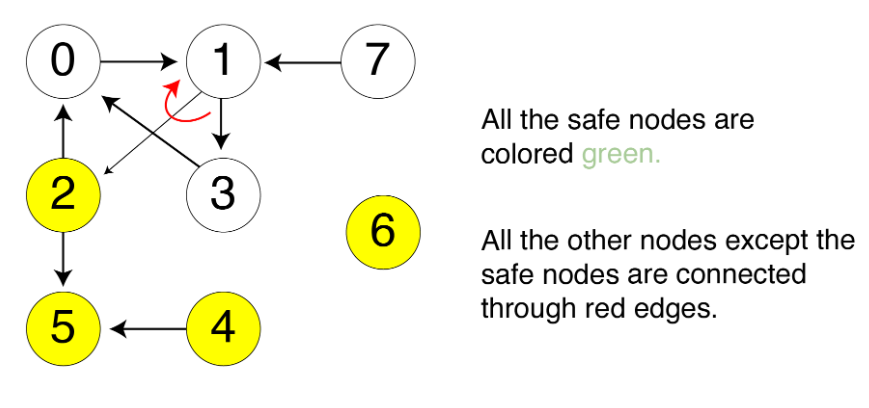
It is clear that these types of nodes will never be considered safe:
- One is which is occurring in a cycle. Example: Nodes 0, 1, and 3.
- Second is which is leading to a cycle. Example: Node 7.
Except these types of nodes, all other nodes will be considered eventually.
Hence in order to find the safe nodes, the unsafe nodes can be detected by checking if they exist or point to a cycle. Now, to solve this using BFS traversal technique, the topological sorting (Kahn's Algorithm) can be used. The topological sort algorithm will automatically exclude the nodes which are either forming a cycle or connected to a cycle.
Transforming the graph:
The node with outdegree 0 is considered as terminal node but the topological sort algorithm deals with the indegrees of the nodes. So, to use the topological sort algorithm, we will reverse every edge of the graph.
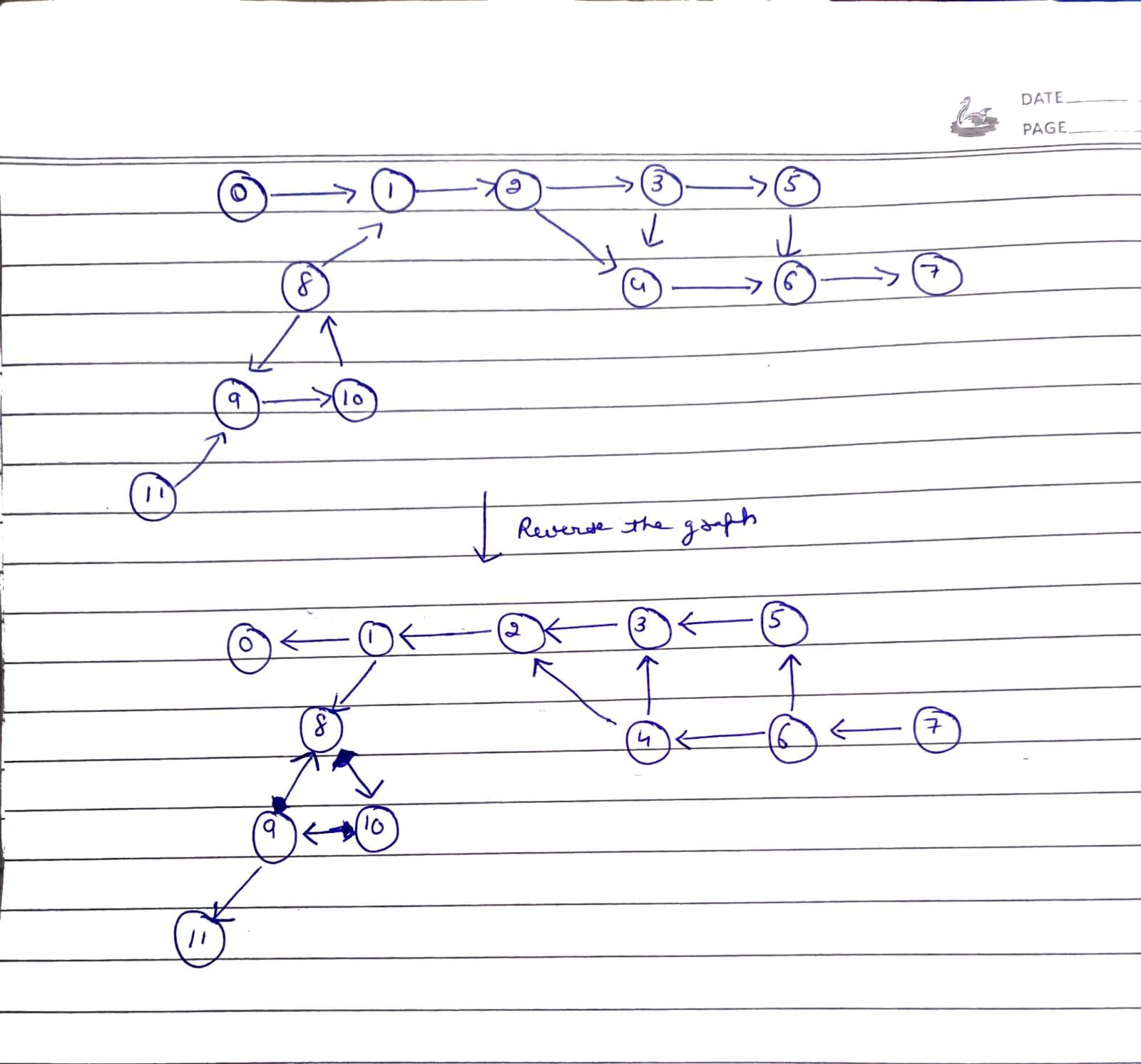
Approach:
- Reverse the edges of the graph reversing the graph.
- Find the topological sort of the reversed graph which will exclude automatically the unsafe nodes.
- Sort the ordering returned by topological sort to obtain the eventually safe nodes in a sorted fashion.
Code:
class Solution {
private:
/* Function to return the topological
sorting of given graph */
vector<int> topoSort(int V, vector<int> adj[]) {
// To store the In-degrees of nodes
vector<int> inDegree(V, 0);
// Update the in-degrees of nodes
for (int i = 0; i < V; i++) {
for(auto it : adj[i]) {
// Update the in-degree
inDegree[it]++;
}
}
// To store the result
vector<int> ans;
// Queue to facilitate BFS
queue<int> q;
// Add the nodes with no in-degree to queue
for(int i=0; i<V; i++) {
if(inDegree[i] == 0) q.push(i);
}
// Until the queue is empty
while(!q.empty()) {
// Get the node
int node = q.front();
// Add it to the answer
ans.push_back(node);
q.pop();
// Traverse the neighbours
for(auto it : adj[node]) {
// Decrement the in-degree
inDegree[it]--;
/* Add the node to queue if
its in-degree becomes zero */
if(inDegree[it] == 0) q.push(it);
}
}
// Return the result
return ans;
}
public:
/* Function to get the
eventually safe nodes */
vector<int> eventualSafeNodes(int V,
vector<int> adj[]) {
// To store the reverse graph
vector<int> adjRev[V];
// Reversing the edges
for (int i = 0; i < V; i++) {
// i -> it, it-> i
for (auto it : adj[i]) {
// Add the edge to reversed graph
adjRev[it].push_back(i);
}
}
/* Return the topological
sort of the given graph */
vector<int> result = topoSort(V, adjRev);
// Sort the result
sort(result.begin(), result.end());
// Return the result
return result;
}
};Complexity Analysis:
- Time Complexity: O(V+E) + O(V*logV) (where V and E represents the number of nodes and edges in the given graph)
- Reversing the graph takes O(E) time.
- Finding topological sort using Kahn's algorithm takes O(V+E) time.
- Sorting the nodes takes O(N*logN) time (where N is the number of safe nodes, which can go up to V in worst-case).
- Space Complexity: O(V+E)
- Storing the reversed graph takes O(E) space.
- Topological sorting algorithm uses extra O(V) space because of in-degrees array and queue data structure.