Problem Statement
Given a string str and a pattern pat, implement a pattern matching function that supports the following special characters:
- '?' Matches any single character.
- '*' Matches any sequence of characters (including the empty sequence).
The pattern must match the entire string.
Examples
Example 1:
Input: str = "xaylmz", pat = "x?y*z"
Output: true
Explanation:
The pattern "x?y*z" matches the string "xaylmz":
- '?' matches 'a'
- '*' matches "lm"
- 'z' matches 'z'Example 2:
Input: str = "xyza", pat = "x*z"
Output: false
Explanation:
The pattern "x*z" does not match the string "xyza" because there is an extra 'a' at the end of the string that is not matched by the pattern.Different Approaches
1️⃣ Recursive Approach
Understanding:
For every index of string S1, we have different options to match that index with string S2. Therefore, we can think in terms of string matching path as we have done already in previous questions.
- Either the characters match already.
- Or, if there is a ‘?’, we can explicitly match a single character.
- For a ‘*’, the following figure explains the scenario end of the string that is not matched by the pattern.
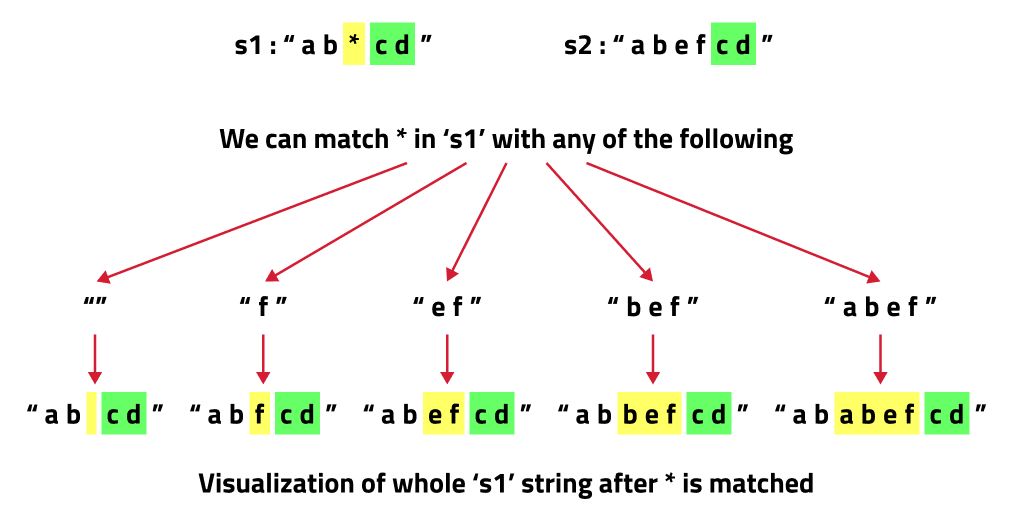
As there is no uniformity in data, there is no other way to find out than to try out all possible ways. To do so we will need to use recursion.
Steps to form the recursive solution:
- Express the problem in terms of indexes: We are given two strings. We can represent them with the help of two indexes i and j. Initially, i=n-1 and j=m-1, where n and m are lengths of strings S1 and S2. Initially, we will call f(n-1,m-1), which means whether string S1[0…n-1] matches with string S2[0…m-1]. f(i, j) returns whether string S1[from index 0 to i] matches S2[from index 0 to j].
- Try out all possible choices at a given index: Now, i and j represent two characters from strings S1 and S2 respectively. There are only two options that make sense: either the characters represented by i and j match or they don’t.
When the characters match: If(
S1[i] == S2[j]), the characters at i and j match, we can simply move to the next characters of both the strings. So we will just decrement both i and j by 1 and recursively find the answer for the remaining string portions. We return f(i-1,j-1). The following figure makes it clear.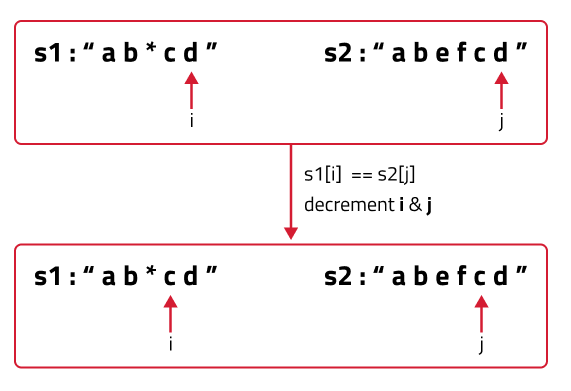
- When the characters don’t match: If the characters don’t match, there are three possible scenarios:
S1[i] == ‘?’: In this case, we can explicitly match ‘?’ at index i of S1 with the corresponding character at index j of S2. And then recursively call f(i-1,j-1) to check for the remaining string.S1[i] == ‘*’: This is an interesting case as now ‘*’ can be replaced with any sequence of characters( of length 0 or more) from S2.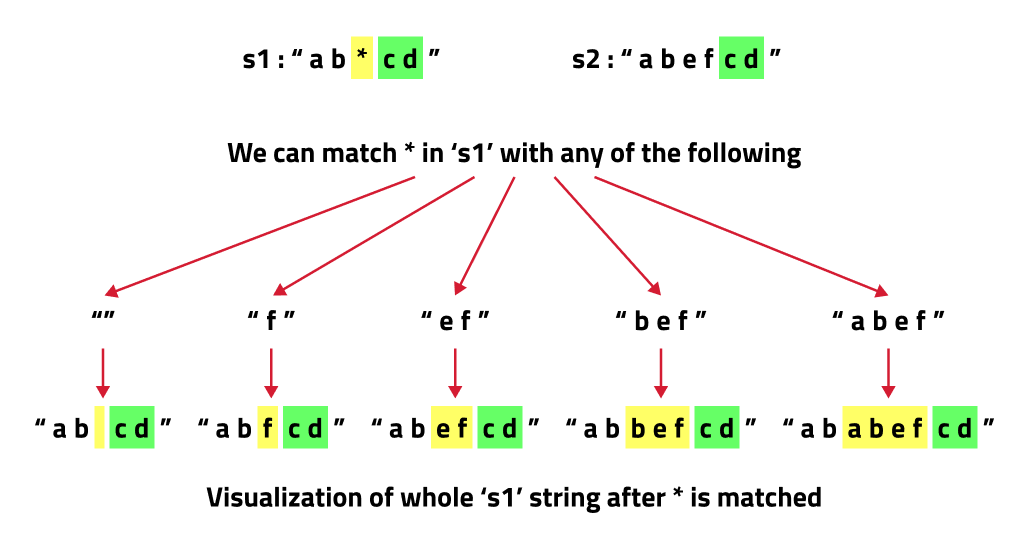
If any of these cases return true, we can say that the characters do match. The next question is how to try all possible ways.
We are using two pointers i and j to represent characters of strings S1 and S2. We can surely write a for loop to compare characters from 0 to j of S2 for the above scenario. Can we do it more smartly? Yes, we can. Please understand the approach explained below.
We are using a recursive function f(i,j). If we do only the following two recursive calls:
- Call f(i-1,j). i.e replace ‘*’ with nothing and act as if it was not present.
Call f(i,j-1). i.e replace ‘*’ with a single character at index j and make the i pointer to still point at index i. In this, we matched it with a single character (one of the many options that need to be tried) and in the next recursive call, as i still point to ‘*’, we get the exact two recursive calls again.
The following recursive tree will help us to understand the recursion better:
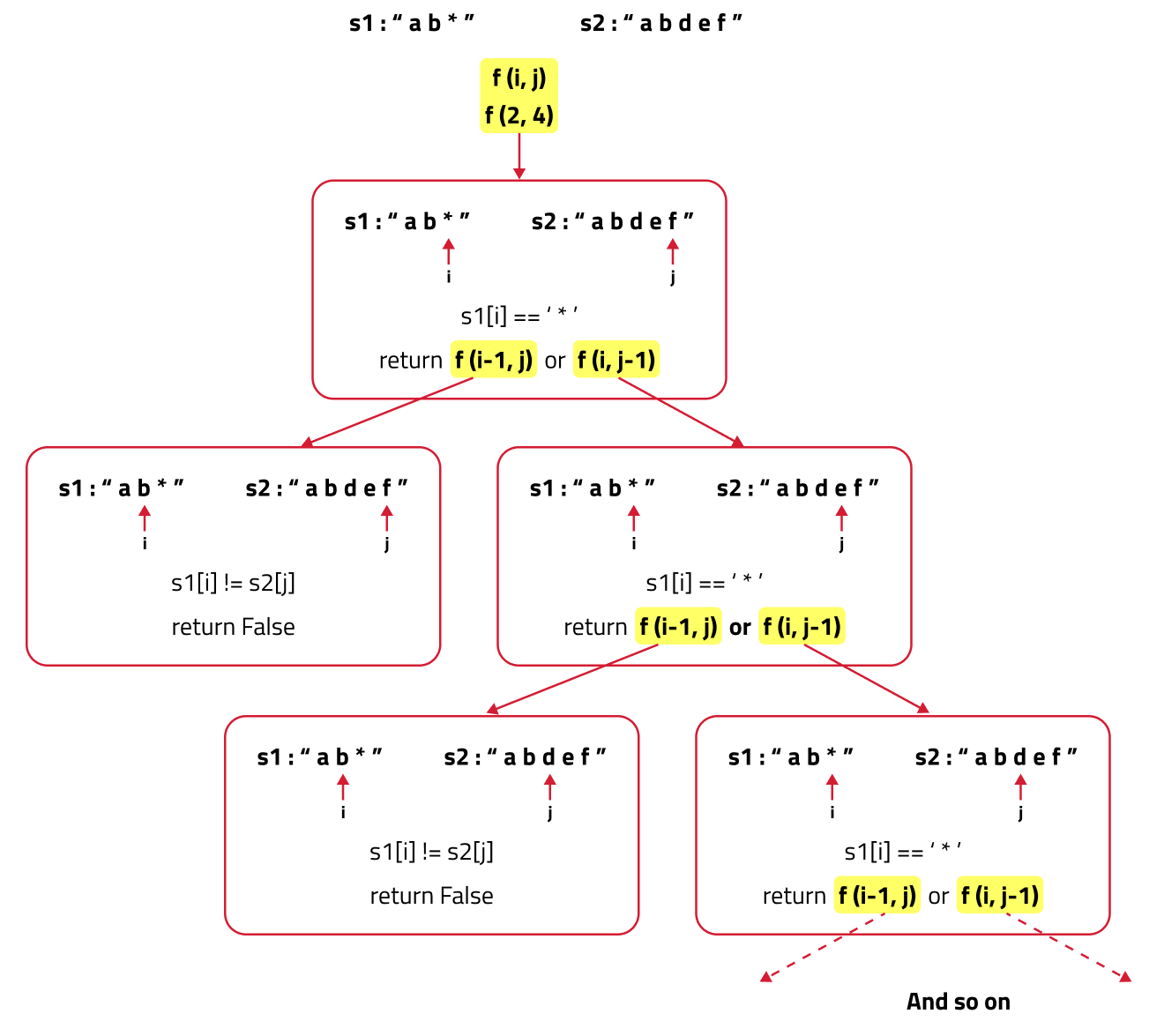
So we see how we can tackle all the required cases associated with ‘*’ by using recursion.
- If S1[i] is neither ‘?’ nor ‘*’: Then we can say as the characters at i and j don’t match then the strings don’t match, so we return false.
- To summarize:
- If S1[i] == ‘?’, return f(i-1,j)
- Else if S1[i] == ‘*’, return f(i-1,j) || f(i,j-1)
Else return false.
/*It is pseudocode and it is not related to any specific programming language */ f(i, j){ if(S1[i] == S2[j] || S1[i] == '?'){ return f(i-1, j-1) } if(S1 == '*'){ return f(i-1, j) || f(i, j-1) } else return false }
- Return logical OR (||) of all the choices: If any of the cases return true, we can say that strings do match. We can use OR operator (||) with the recursive calls.
- Base Cases: We are reducing i and j in our recursive relation, there can be two possibilities, either i becomes -1 or j becomes -1., i,e we exhaust either S1 or S2 respectively.
- When S1 is exhausted: When S1 is exhausted (i<0), we know that in order for the strings to match, String S2 should also exhaust simultaneously. If it does, we return true, else we return false. We can say, if(i<0 && j<0), return true and if(i<0 && j>=0), return false.
- When S2 is exhausted: When S2 is exhausted(j<0) and S1 has not, there is only one pattern that can account for true(matching of strings). It is if S1 is like this “*”, ”****”, ”***”, i.e: S1 contains only stars. Then we can replace every star with a sequence of length 0 and say that the string match. If S1 is all-stars, we return true, else return false.
Code:
#include <bits/stdc++.h>
using namespace std;
class Solution {
public:
/**
* Helper function for recursive wildcard pattern matching.
*
* @param str The input string.
* @param pattern The pattern string which may include '?' and '*'.
* @param strIndex Current index in the input string.
* @param patIndex Current index in the pattern string.
* @return True if the pattern matches the string, otherwise false.
*/
bool recursiveMatch(string& str, string& pattern, int strIndex, int patIndex) {
// Base Case: Both string and pattern are exhausted.
if (strIndex < 0 && patIndex < 0) {
return true;
}
// Base Case: Pattern is exhausted but string is not.
if (patIndex < 0 && strIndex >= 0) {
return false;
}
// Base Case: String is exhausted but pattern is not.
if (strIndex < 0 && patIndex >= 0) {
// Remaining pattern must only contain '*'.
for (int i = patIndex; i >= 0; i--) {
if (pattern[i] != '*') {
return false;
}
}
return true;
}
// Case 1: Characters match or pattern has '?'.
if (str[strIndex] == pattern[patIndex] || pattern[patIndex] == '?') {
return recursiveMatch(str, pattern, strIndex - 1, patIndex - 1);
}
// Case 2: Pattern has '*'.
if (pattern[patIndex] == '*') {
// Match current character or skip '*'.
return recursiveMatch(str, pattern, strIndex - 1, patIndex) ||
recursiveMatch(str, pattern, strIndex, patIndex - 1);
}
// Case 3: Characters don't match and pattern is not '?' or '*'.
return false;
}
/**
* Function to check if the pattern matches the string.
*
* @param str The input string.
* @param pattern The pattern string which may include '?' and '*'.
* @return True if the pattern matches the string, otherwise false.
*/
bool wildCard(string str, string pattern) {
// Convert string and pattern to reference types for recursive function.
return recursiveMatch(str, pattern, str.length() - 1, pattern.length() - 1);
}
};
int main() {
string str = "abcde";
string pattern = "a*e";
// Create an instance of the Solution class.
Solution solution;
// Check if the pattern matches the string.
bool result = solution.wildCard(str, pattern);
// Print the result.
cout << "Does the pattern match the string? " << (result ? "Yes" : "No") << endl;
return 0;
}
Complexity Analysis:
- Time Complexity: Exponential
- Space Complexity:
O(N+M), we are using a stack space of N+M.
2️⃣ Memoization
If we draw the recursion tree, we will see that there are overlapping subproblems. Hence the DP approaches can be applied to the recursive solution.
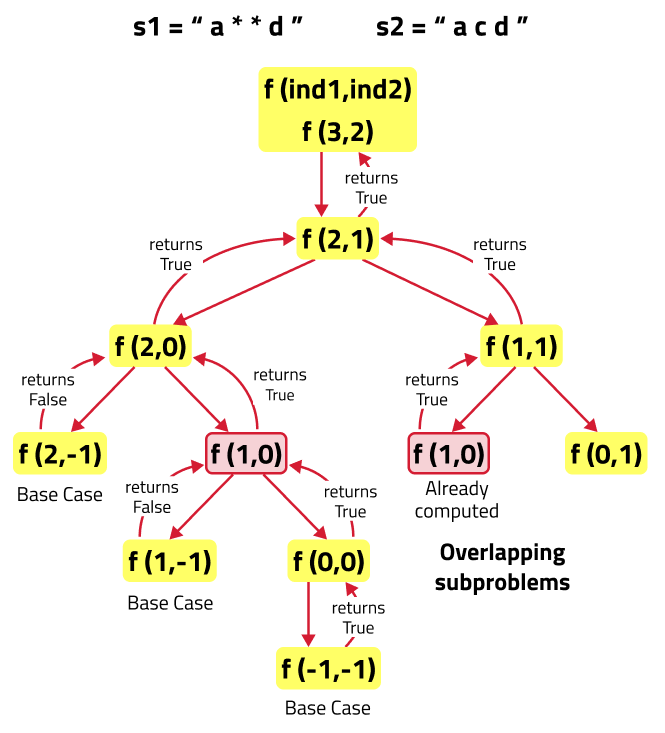
In order to convert a recursive solution to memoization the following steps will be taken:
- Declare a dp array of size [n][m]: As there are two changing parameters in the recursive solution, 'i' and 'j'. The maximum value 'i' can attain is 'n-1', where n is the size of string S1 and 'j' can take maximum value of 'm-1', where m is the size of string S2. Therefore, we need 2D dp array.
- The dp array stores the calculations of subproblems. Initialize dp array with -1, to indicate that no subproblem has been solved yet.
- While encountering an overlapping subproblem: When we come across a subproblem, for which the dp array has value other than -1, it means we have found a subproblem which has been solved before hence it is an overlapping subproblem. No need to calculate it's value again just retrieve the value from dp array and return it.
- Store the value of subproblem: Whenever, a subproblem is encountered and it is not solved yet(the value at this index will be -1 in the dp array), store the calculated value of subproblem in the array.
Code:
#include <bits/stdc++.h>
using namespace std;
class Solution {
public:
/**
* Helper function for recursive wildcard pattern matching with memoization.
*
* @param text The input text string.
* @param pattern The pattern string which may include '?' and '*'.
* @param textIndex Current index in the input text string.
* @param patternIndex Current index in the pattern string.
* @param dp Memoization table to store intermediate results.
* @return True if the pattern matches the text, otherwise false.
*/
bool matchHelper(string& text, string& pattern, int textIndex, int patternIndex, vector<vector<int>>& dp) {
// Base Case: Both text and pattern are exhausted.
if (textIndex < 0 && patternIndex < 0) {
return true;
}
// Base Case: Pattern is exhausted but text is not.
if (patternIndex < 0 && textIndex >= 0) {
return false;
}
// Base Case: Text is exhausted but pattern is not.
if (textIndex < 0 && patternIndex >= 0) {
// Remaining pattern must only contain '*'.
for (int i = patternIndex; i >= 0; i--) {
if (pattern[i] != '*') {
return false;
}
}
return true;
}
// Check memoization table.
if (dp[textIndex][patternIndex] != -1) {
return dp[textIndex][patternIndex];
}
// Case 1: Characters match or pattern has '?'.
if (text[textIndex] == pattern[patternIndex] || pattern[patternIndex] == '?') {
return dp[textIndex][patternIndex] = matchHelper(text, pattern, textIndex - 1, patternIndex - 1, dp);
}
// Case 2: Pattern has '*'.
if (pattern[patternIndex] == '*') {
// Match current character or skip '*'.
return dp[textIndex][patternIndex] = (matchHelper(text, pattern, textIndex - 1, patternIndex, dp) ||
matchHelper(text, pattern, textIndex, patternIndex - 1, dp));
}
// Case 3: Characters don't match and pattern is not '?' or '*'.
return dp[textIndex][patternIndex] = false;
}
/**
* Function to check if the pattern matches the text.
*
* @param text The input text string.
* @param pattern The pattern string which may include '?' and '*'.
* @return True if the pattern matches the text, otherwise false.
*/
bool wildCard(string pattern, string text) {
// Create a memoization table initialized with -1.
vector<vector<int>> dp(text.length(), vector<int>(pattern.length(), -1));
// Start matching from the end of both strings.
return matchHelper(text, pattern, text.length() - 1, pattern.length() - 1, dp);
}
};
int main() {
string text = "abcde";
string pattern = "a*e";
// Create an instance of the Solution class.
Solution solution;
// Check if the pattern matches the text.
bool result = solution.wildCard(pattern, text);
// Print the result.
cout << "Does the pattern match the text? " << (result ? "Yes" : "No") << endl;
return 0;
}
Complexity Analysis:
- Time Complexity:
O(N*M), Where N is the length of string S1 and M is the length of string S2. There are N*M states therefore at max ‘N*M’ new problems will be solved. - Space Complexity:
O(N*M) + O(N+M), We are using a recursion stack space(O(N+M)) and a 2D array (O(N*M)).
