Problem Statement

Given an array of non-negative integers, height representing the elevation of ground. Calculate the amount of water that can be trapped after rain.

Examples

Example 1:

Input: height = [0, 1, 0, 2, 1, 0, 1, 3, 2, 1, 2, 1]
Output: 6

Explanation: From the diagram we can conclude,
1 + 1 + 2 + 1 + 1 = 6 unit of water can be trapped.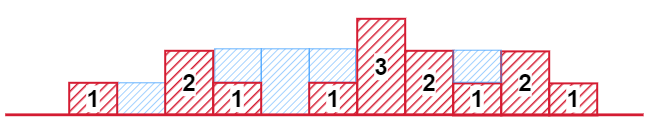

Example 2:

Input: height = [4, 2, 0, 3, 2, 5]
Output: 9

Different Approaches

1️⃣ Brute Force Approach

Intuition:

Imagine looking at the ground from a side view after a heavy rain. Water gets trapped in the dips and valleys between the heights. To determine the amount of trapped water, it's essential to know the highest barriers to the left and right of each position. These barriers will are important to understand how much water can sit atop each element.

By knowing the maximum heights to the left and right of each position, the water level at that position will be determined by the shorter of these two barriers. The difference between this water level and the height of the ground at that position will give the amount of water trapped there.

Understanding:

Traversing to the left and right side to get the maximum for every height of ground is inefficient. To solve this problem efficiently, two auxiliary arrays will be used to store the maximum heights to the left and right of each position:

• Prefix Maximum Array: Stores the maximum of all the elements to the left till the current index.
• Suffix Maximum Array: Stores the maximum of all the elements to the right from the current index.

Approach:

1. Store the maximum height from the start to each position in this array. This will help in determining the maximum height to the left of any position.
2. Store the maximum height from each position to the end of the array in this array. This will help in determining the maximum height to the right of any position.
3. Traverse the array and for each position, determine the water level using the minimum of the prefix and suffix maximum heights. Subtract the ground height at that position from this water level to calculate the trapped water at that position.
4. Sum all these values to get the total trapped water.

Code:

class Solution
{
public:
    // Helper function to calculate left max for every index
    vector<int> getLeftMax(vector<int>& height) {
        vector<int> ans(height.size()); // Step 1: Create a vector to store left max values
        int maxi = INT_MIN;             // Step 2: Initialize maximum as the smallest integer

        // Step 3: Traverse from left to right
        for (int i = 0; i < height.size(); i++) {
            maxi = max(maxi, height[i]);  // Update maxi so far
            ans[i] = maxi;                // Store it in the answer vector
        }

        return ans; // Step 4: Return the left max array
    }

    // Helper function to calculate right max for every index
    vector<int> getRightMax(vector<int>& height) {
        vector<int> ans(height.size()); // Step 1: Create a vector to store right max values
        int maxi = INT_MIN;             // Step 2: Initialize maximum as the smallest integer

        // Step 3: Traverse from right to left
        for(int i = height.size() - 1; i >= 0; i--) {
            maxi = max(maxi, height[i]);  // Update maxi so far
            ans[i] = maxi;                // Store it in the answer vector
        }

        return ans; // Step 4: Return the right max array
    }

    // Main function to calculate trapped rainwater
    int trap(vector<int> &height) {
        // Step 1: Get the maximum height to the left of each index
        vector<int> leftMax = getLeftMax(height);

        // Step 2: Get the maximum height to the right of each index
        vector<int> rightMax = getRightMax(height);

        int capacity = 0; // Step 3: Initialize total trapped water to 0

        // Step 4: Traverse the height array to calculate water at each index
        for (int i = 0; i < height.size(); i++) {
            // Minimum of left max and right max determines the water level
            // Subtract height[i] to get trapped water at that index
            capacity += min(leftMax[i], rightMax[i]) - height[i];
        }

        // Step 5: Return the total trapped water
        return capacity;
    }
};

Complexity Analysis:

• Time Complexity:O(N) (where N is the size of given array)
  • Calculating the Prefix and Suffix Maximum Arrays take O(N) time each.
  • Traversing on the given array once takes O(N) time.
• Space Complexity:O(N)
  • Storing the Prefix and Suffix Maximum Arrays takes O(N) space each.

2️⃣ Optimal Approach (Two Pointers)

Intuition:

In earlier solution, storing the prefix and suffix maximums was taking extra space. However, at a particular height, only the minimum height (out of the left maximum height and right maximum height) was considered. This simple means that at a particular moment either the left maximum height or the right maximum height was useful.

Understanding:

It is impossible to find out the left and right barriers beforehand, but a clever way to traverse the array is by traversing it from both ends. The left and right maximum heights (barriers) can be maintained and based on these values the water on top of current height can be calculated using the formula:
          water = min(leftMax, rightMax) - height,
where height is the height of current ground.
This gives an idea of using two pointers that start from both ends of the array while maintaining the left and right barriers (maximum heights). Since, only the lower barrier (minimum height) is considered, out of the two pointers, only one (having minimum height) will move at a time which ensures that no potential taller height is missed.

Approach:

1. Start with two pointers at the beginning and end of the array. Maintain two variables to keep track of the maximum heights encountered so far from both directions.
2. Use a loop to move the pointers towards each other until they meet. Compare the heights at the current positions of the pointers.
3. If the height at the left pointer is less than or equal to the height at the right pointer:
   1. If the current height is less than the maximum height on the left, calculate the water trapped and add to the total.
   2. Otherwise, update the maximum height on the left. Move the left pointer to the right.
4. If the height at the right pointer is less:
   1. If the current height is less than the maximum height on the right, calculate the water trapped and add to the total.
   2. Otherwise, update the maximum height on the right. Move the right pointer to the left.
5. Once the pointers meet, return the total trapped water.

Code:

 class Solution {
public:
    int trap(vector<int>& height) {
        int left = 0;                         // Pointer from the start
        int right = height.size() - 1;        // Pointer from the end
        int leftMax = 0, rightMax = 0;        // Track max height from both sides
        int capacity = 0;                     // Total water trapped

        // Traverse until both pointers meet
        while (left < right) {
            // Case 1: Height at left is smaller
            if (height[left] < height[right]) {
                // Update leftMax or calculate trapped water at left
                if (height[left] >= leftMax) {
                    leftMax = height[left];   // Update max seen so far from left
                } else {
                    capacity += leftMax - height[left]; // Water trapped = leftMax - height
                }
                left++; // Move left pointer inward
            } 
            // Case 2: Height at right is smaller or equal
            else {
                // Update rightMax or calculate trapped water at right
                if (height[right] >= rightMax) {
                    rightMax = height[right]; // Update max seen so far from right
                } else {
                    capacity += rightMax - height[right]; // Water trapped = rightMax - height
                }
                right--; // Move right pointer inward
            }
        }

        return capacity; // Final water trapped
    }
};

Complexity Analysis:

• Time Complexity:O(N) (where N is the size of given array)
  • The left and right pointers will traverse the whole array in total taking O(N) time.
• Space Complexity:O(1)
  Using only a couple of variables.