Problem Statement
Given an integer array of coins representing coins of different denominations and an integer target representing a total amount of money. Return the fewest number of coins that are needed to make up that target. If that amount of money cannot be made up by any combination of the coins, return -1. There are infinite numbers of coins of each type.
LeetCode:
Constraints:
1 <= coins.length <= 12
1 <= coins[i] <= 2^31 - 1
0 <= amount <= 10^4Examples
Example 1:
Input: Target = 11, Coins = [1, 2, 5]
Output: 3
Explanation:
Minimum Number of Coins: 3 (2 coins of 5, and 1 coin of 1)Example 2:
Input: coins = [2, 5], Target = 3
Output: -1
Explanation: It's not possible to make target 3 with coins of 2 and 5.
Since we can't combine the coin 2 and 5 to make the target 3.
So the output is -1.Different Approaches
1️⃣ Recursive Approach
Why a Greedy Solution will not work:
As the question asks for minimum number of coins, the first approach that comes to our mind is greedy. A greedy solution will fail in this problem because there is no ‘uniformity’ in data. While selecting a local better choice we may choose an item that will in the long term give less value.
A Greedy solution will be to take the highest denomination coin first, so we will take an item on index 0, with a value of 9. Now the remaining target sum will be 2. Therefore we can only consider coins with a value of 1. We will take 2 coins of value 1 to meet the target. So a greedy solution gives us the answer 3 (9,1,1).
Now we can clearly see that a non-greedy solution of taking 2 coins (6,5) gives a better option. So we can say that the greedy solution doesn’t work for this problem.
As the greedy approach doesn’t work, try to generate all possible combinations using recursion and select the combination which gives the minimum number of coins.
Steps to form the recursive solution:
- Express the problem in terms of indexes: We are given ‘n’ distinct numbers, where n is the length of the array. Their denomination is represented by the ‘coins’ array. So clearly one parameter will be ‘ind’, i.e index up to which the array items are being considered. There is one more parameter “T”, to know the given target that we want to achieve.
- So, initially, we need to find f(n-1, T) where T is the initial target given. f(n-1, T) will give the minimum number of coins required to form the target sum by considering coins from index 0 to n-1.
- Try out all possible choices at a given index: As all the subsets needs to be generated, use the pick/non-pick technique. There will be a slight change for this question which is discussed below.
We have two choices:- Exclude the current element in the subset: First try to find a subset without considering the current index coin. If the current coin is excluded, the target sum will not be affected and the number of coins added to the solution will be 0. So call the recursive function f(ind-1, T).
- Include the current element in the subset: Try to find a subset by considering the current icoin. As the current coin is included, the target sum will be updated to T-arr[ind], as we have considered 1 coin to be part of the solution.
- Now here is the catch, as there is an unlimited supply of coins, we want to again form a solution with the same coin value. So we will not recursively call for f(ind-1, T-arr[ind]) rather we will stay at that index only and call for f(ind, T-arr[ind]) to find the answer.
Note: Consider the current coin only when its denomination value (arr[ind]) is less than or equal to the target T.
f(ind, T){
notTake = 0 + f(ind-1, T)
take = 1e9
if(arr[ind] <= T)
take = 1 + f(ind, T-arr[ind])
}- Return the minimum of two choices: As we have to return the minimum number of coins, we will return the minimum of take and notTake as our answer.
f(ind, T){
notTake = 0 + f(ind-1, T)
take = 1e9
if(arr[ind] <= T)
take = 1 + f(ind, T-arr[ind])
return min(take, notTake)
}- Base Case: If ind==0, it means we are at the first item, so in that case, the following cases can arise:
- In cases where the target is divisible by the coin element, return (T / arr[0]), as this will give the number of coins needed to make target.
- In all other cases, where the target is not divisible by the coin, a solution can not be formed, so return a big number like 1e9. This will prevent the coin from getting added to the final solution as we need to return the minimum number of coins.
Code:
#include <bits/stdc++.h>
using namespace std;
class Solution {
private:
/**
* Helper function to calculate the minimum number of coins
* needed to form the target amount using recursion.
* @param coins Vector of coin denominations.
* @param index Current index in the coin array.
* @param target Remaining amount to be formed.
* @return Minimum number of coins required to form the target.
*/
int findMinCoins(vector<int>& coins, int index, int target) {
// Base case: If we're at the first coin
if (index == 0) {
// If target is divisible by the coin value, return the quotient
return (target % coins[0] == 0) ? target / coins[0] : 1e9;
}
// Do not take the current coin
int notTaken = findMinCoins(coins, index - 1, target);
// Take the current coin if it does not exceed the target
int taken = 1e9; // Initialize to a large value
if (coins[index] <= target) {
taken = 1 + findMinCoins(coins, index, target - coins[index]);
}
// Return the minimum of taking or not taking the coin
return min(notTaken, taken);
}
public:
/**
* Function to calculate the minimum number of coins needed to form the target amount.
* @param coins Vector of coin denominations.
* @param amount Target amount to be formed.
* @return Minimum number of coins required, or -1 if not possible.
*/
int minimumCoins(vector<int>& coins, int amount) {
int n = coins.size();
// Use the helper function to compute the result
int result = findMinCoins(coins, n - 1, amount);
// If the result is still a large value, it's not possible to form the amount
return (result >= 1e9) ? -1 : result;
}
};
int main() {
vector<int> coins = {1, 2, 3}; // Coin denominations
int amount = 7; // Target amount
// Create an instance of the Solution class
Solution solution;
// Calculate and print the result
int result = solution.minimumCoins(coins, amount);
if (result != -1) {
cout << "The minimum number of coins needed is " << result << endl;
} else {
cout << "It is not possible to form the target amount with the given coins." << endl;
}
return 0;
}class Solution {
public:
int recursive(vector<int>& coins, int index, int amount) {
// Base case: no coins needed if amount is 0
if (amount == 0) return 0;
// Invalid path: return large number to represent impossible case
if (index >= coins.size() || amount < 0) return 1e9;
// Include the coin at index (stay at same index, because infinite supply)
int include = 1 + recursive(coins, index, amount - coins[index]);
// Exclude the coin and move to next
int exclude = recursive(coins, index + 1, amount);
return min(include, exclude); // choose min of both
}
int MinimumCoins(vector<int>& coins, int amount) {
int res = recursive(coins, 0, amount);
return res >= 1e9 ? -1 : res; // if res is still large, it means impossible
}
};
Complexity Analysis:
- Time Complexity:
O(2^n), as each element has 2 choices, and there arenelements in the array. - Space Complexity:
O(n)- The stack space will be
O(n), the maximum depth of the stack.
- The stack space will be
Intuition:
- Start with the target amount:
- You start with your target amount and explore all possible combinations of coins to find the minimum number of coins needed to make that amount.
- For each coin denomination:
- You have two choices:
- Include the current coin denomination:
- You include the current coin denomination and recursively find the minimum number of coins needed for the remaining target amount.
- Exclude the current coin denomination:
- You exclude the current coin denomination and move on to the next denomination.
- Include the current coin denomination:
- You have two choices:
- Explore all possible combinations:
- You recursively explore all possible combinations by including or excluding each coin denomination until the target amount becomes 0.
- Return the minimum number of coins needed:
- Once the target amount becomes 0, you return the minimum number of coins needed to make that amount.
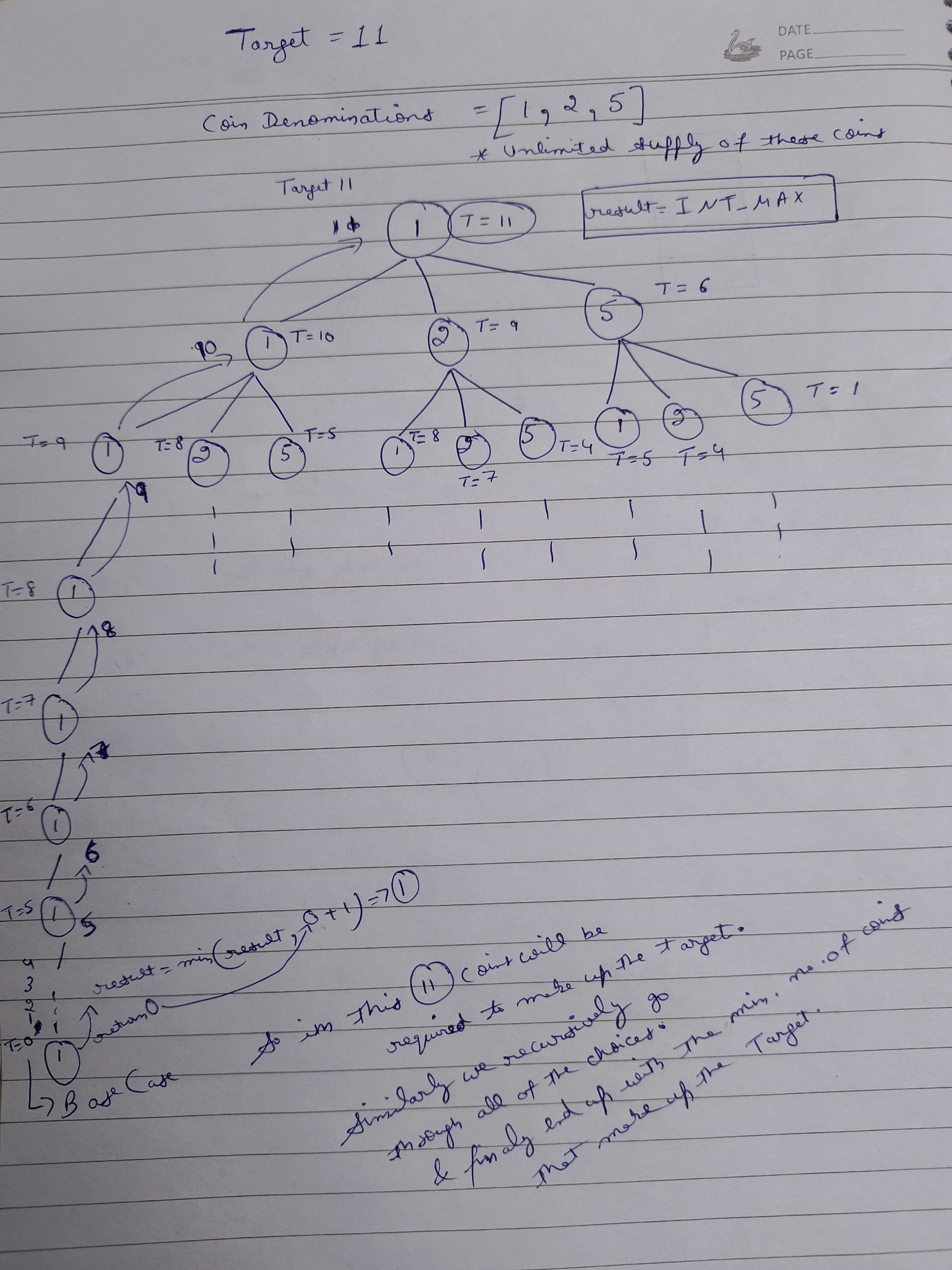
Visualization:
minCoins(11)
| \
minCoins(10) minCoins(9)
| / \
minCoins(9) minCoins(8) minCoins(6)
| / | / \
minCoins(8) minCoins(7) minCoins(4)
... ... ... ...
2️⃣ Top-Down Approach (Memoization)
If we draw the recursion tree, we will see that there are overlapping subproblems. Hence the DP approaches can be applied to the recursive solution.
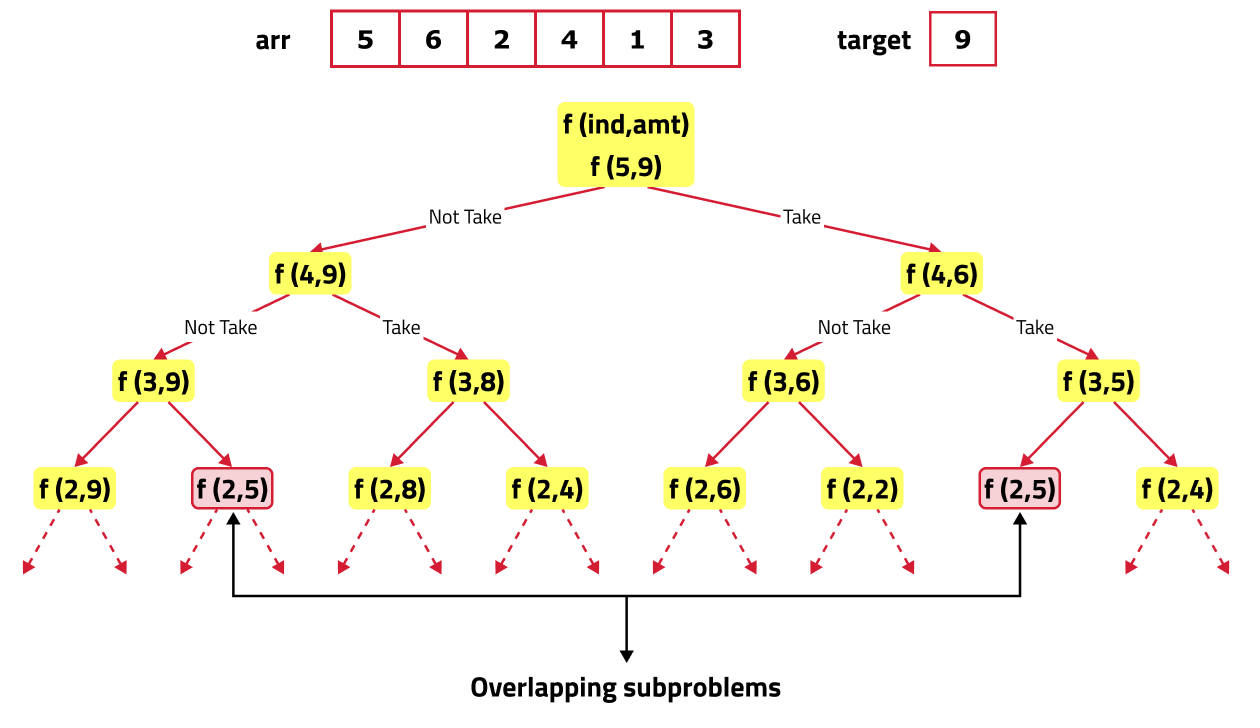
In order to convert a recursive solution to memoization the following steps will be taken:
- Declare a dp array of size [n][target+1]: As there are two changing parameters in the recursive solution, 'ind' and 'target'. The maximum value 'ind' can attain is (n), where n is the size of array and for 'target' only values between 0 to target. Therefore, we need 2D dp array.
- The dp array stores the calculations of subproblems. Initialize dp array with -1, to indicate that no subproblem has been solved yet.
- While encountering an overlapping subproblem: When we come across a subproblem, for which the dp array has value other than -1, it means we have found a subproblem which has been solved before hence it is an overlapping subproblem. No need to calculate it's value again just retrieve the value from dp array and return it.
- Store the value of subproblem: Whenever, a subproblem is encountered and it is not solved yet(the value at this index will be -1 in the dp array), store the calculated value of subproblem in the array.
Code:
#include <bits/stdc++.h>
using namespace std;
class Solution {
private:
/**
* Helper function to calculate the minimum number of coins
* needed to form the target amount using memoization.
* @param coins Vector of coin denominations.
* @param index Current index in the coin array.
* @param target Remaining amount to be formed.
* @param dp Memoization table to store intermediate results.
* @return Minimum number of coins required to form the target.
*/
int findMinCoins(vector<int>& coins, int index, int target, vector<vector<int>>& dp) {
// Base case: If we're at the first coin
if (index == 0) {
// If target is divisible by the coin value, return the quotient
return (target % coins[0] == 0) ? target / coins[0] : 1e9;
}
// If already computed, return the stored value
if (dp[index][target] != -1) {
return dp[index][target];
}
// Do not take the current coin
int notTaken = findMinCoins(coins, index - 1, target, dp);
// Take the current coin if it does not exceed the target
int taken = 1e9; // Initialize to a large value
if (coins[index] <= target) {
taken = 1 + findMinCoins(coins, index, target - coins[index], dp);
}
// Store the result in the dp table and return it
return dp[index][target] = min(notTaken, taken);
}
public:
/**
* Function to calculate the minimum number of coins needed to form the target amount.
* @param coins Vector of coin denominations.
* @param amount Target amount to be formed.
* @return Minimum number of coins required, or -1 if not possible.
*/
int minimumCoins(vector<int>& coins, int amount) {
int n = coins.size();
// Create a memoization table initialized to -1
vector<vector<int>> dp(n, vector<int>(amount + 1, -1));
// Use the helper function to compute the result
int result = findMinCoins(coins, n - 1, amount, dp);
// If the result is still a large value, it's not possible to form the amount
return (result >= 1e9) ? -1 : result;
}
};
int main() {
vector<int> coins = {1, 2, 3}; // Coin denominations
int amount = 7; // Target amount
// Create an instance of the Solution class
Solution solution;
// Calculate and print the result
int result = solution.minimumCoins(coins, amount);
if (result != -1) {
cout << "The minimum number of coins needed is " << result << endl;
} else {
cout << "It is not possible to form the target amount with the given coins." << endl;
}
return 0;
}#include <bits/stdc++.h>
using namespace std;
class Solution {
public:
// Memoized recursive helper function
int recursive(vector<int>& coins, int index, int amount, vector<vector<int>>& dp) {
// ✅ Base case 1: Exact amount achieved
if (amount == 0) return 0;
// ❌ Base case 2: Index out of bounds or amount went negative
if (index >= coins.size() || amount < 0) return 1e9;
// 🧠 Step 1: Check if result is already computed
if (dp[index][amount] != -1) return dp[index][amount];
// ✅ Step 2: Option 1 - Include the current coin (stay at same index)
int include = 1 + recursive(coins, index, amount - coins[index], dp);
// ✅ Step 3: Option 2 - Exclude the current coin (move to next index)
int exclude = recursive(coins, index + 1, amount, dp);
// ✅ Step 4: Store and return the minimum of include/exclude
return dp[index][amount] = min(include, exclude);
}
int MinimumCoins(vector<int>& coins, int amount) {
int n = coins.size();
// 📦 Step 0: Create a DP table and initialize with -1
vector<vector<int>> dp(n, vector<int>(amount + 1, -1));
int res = recursive(coins, 0, amount, dp);
// 🧾 Step 5: Handle case when no valid combination was found
return res >= 1e9 ? -1 : res;
}
};
Complexity Analysis:
- Time Complexity:
O(N*Target), as there areN*Targetstates therefore at max ‘N*Target’ new problems will be solved. - Space Complexity:
O(N*Target) + O(N), the stack space will be O(N) and a 2D array of size N*T is used.
3️⃣ Tabulation (Bottom-up Approach)
#include <bits/stdc++.h>
using namespace std;
class Solution {
public:
int MinimumCoins(vector<int>& coins, int amount) {
int n = coins.size();
// Step 1: Create a 2D DP table
// dp[i][j] represents the minimum number of coins needed to make amount 'j' using first 'i+1' coins
vector<vector<int>> dp(n, vector<int>(amount + 1, 1e9)); // Initialize with large value (1e9) indicating not possible initially
// Step 2: Base Case - amount 0 requires 0 coins for all rows
for (int i = 0; i < n; i++) {
dp[i][0] = 0;
}
// Step 3: Fill the first row (only using coins[0])
// If amount is divisible by coins[0], it can be formed using only that coin
for (int target = 1; target <= amount; target++) {
if (target % coins[0] == 0) {
dp[0][target] = target / coins[0]; // Use coin[0] multiple times
}
// Else, remains as 1e9 (impossible)
}
// Step 4: Fill the rest of the DP table
// Try to form each amount using coins[0..i]
for (int i = 1; i < n; i++) {
for (int target = 1; target <= amount; target++) {
int notTake = dp[i - 1][target]; // Don't use coin[i]
int take = 1e9;
// Check if we can take coin[i]
if (coins[i] <= target) {
take = 1 + dp[i][target - coins[i]]; // Take coin[i] and stay at same row (unbounded)
}
// Step 5: Take the minimum of including or excluding current coin
dp[i][target] = min(take, notTake);
}
}
// Step 6: Return final answer from bottom-right cell
int ans = dp[n - 1][amount];
return ans >= 1e9 ? -1 : ans; // If still 1e9, means not possible to form the amount
}
};
Complexity Analysis:
- Time Complexity:
O(n * amount) - Space Complexity:
O(n * amount)
4️⃣ Space Optimized Approach
Code:
int MinimumCoins(vector<int>& coins, int amount) {
int n = coins.size();
// Step 1: Create a 1D array to represent the previous row of the DP table
// prev[j] = minimum coins needed to make sum j using the first i coins
vector<int> prev(amount + 1, 1e9);
// Base case: To make amount 0, we need 0 coins
prev[0] = 0;
// Step 2: Initialize the base row using only coins[0]
// If the amount is divisible by coins[0], then it's possible to form it
// by using coin[0] multiple times
for (int target = 1; target <= amount; target++) {
if (target % coins[0] == 0) {
prev[target] = target / coins[0]; // number of times we need coin[0]
}
// If not divisible, value remains 1e9 (impossible)
}
// Step 3: Process remaining coins one by one (starting from 2nd coin)
for (int i = 1; i < n; i++) {
// Create a new array to store current row results
vector<int> curr(amount + 1, 1e9);
curr[0] = 0; // base case: 0 coins needed to make 0 amount
// Step 4: For each amount from 1 to 'amount'
for (int target = 1; target <= amount; target++) {
int include = 1e9;
// Option 1: Include current coin (if it doesn't exceed the amount)
// Since we can use the same coin unlimited times,
// stay at 'i' and reduce the target
if (coins[i] <= target) {
include = 1 + curr[target - coins[i]];
}
// Option 2: Exclude current coin, take answer from previous row
int exclude = prev[target];
// Step 5: Take the minimum of both choices
curr[target] = min(include, exclude);
}
// Move current row to previous row for next iteration
prev = curr;
}
// Step 6: Final answer is in prev[amount]
return (prev[amount] >= 1e9) ? -1 : prev[amount];
}
Complexity Analysis:
- Time Complexity:
O(n * amount) - Space Complexity:
O(2* amount)
