Problem Statement

Given the root of a binary tree, invert the tree, and return its root.

LeetCode:

• Invert Binary Tree

Constraints:

• The number of nodes in the tree is in the range [0, 100].
• -100 ≤ Node.val ≤ 100

Examples

Example 1:

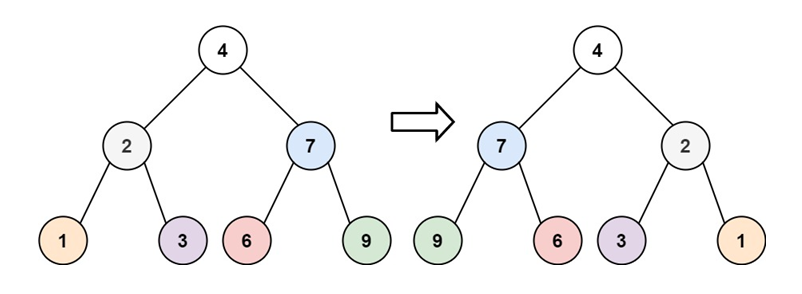
Input: root = [4, 2, 7, 1, 3, 6, 9]
Output: [4, 7, 2, 9, 6, 3, 1]

Example 2:

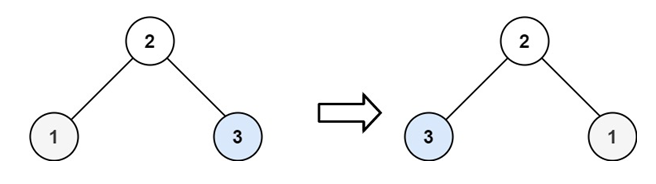
Input: root = [2, 1, 3]
Output: [2, 3, 1]

Example 3:

Input: root = []
Output: []

Different Approaches

1️⃣ Recursive Approach

Intuition:

Recursively visit each node in post-order fashion (or pre-order), swap its left and right children, and continue down the tree.

Approach:

1. If the current node is nullptr, return.
2. Swap the left and right child nodes.
3. Recursively do the same for the new left and right childen.

Code:

class Solution {
public:
    TreeNode* invertTree(TreeNode* root) {
        if (root == nullptr) return nullptr;

        // Swap the left and right children
        swap(root->left, root->right);

        // Recur for left and right subtrees
        invertTree(root->left);
        invertTree(root->right);

        return root;
    }
};

Complexity Analysis:

• Time Complexity:O(n)
  • Every node is visited once.
• Space Complexity:O(h)
  • h is the height of the tree due to the call stack. Worst case O(n), best case O(log n) for balanced trees.

2️⃣ Iterative Approach (Using Queue - BFS)

Intuition:

Use level-order traversal (BFS) with a queue. At each node, swap the left and right children.

Approach:

1. Initialize a queue and push the root.
2. While the queue is not empty.
   1. Pop a node from the queue.
   2. Swap its left and right children.
   3. Push non-null children into the queue.

Code:

#include <queue>
class Solution {
public:
    TreeNode* invertTree(TreeNode* root) {
        if (root == nullptr) return nullptr;

        std::queue<TreeNode*> q;
        q.push(root);

        while (!q.empty()) {
            TreeNode* current = q.front();
            q.pop();

            // Swap left and right
            swap(current->left, current->right);

            if (current->left) q.push(current->left);
            if (current->right) q.push(current->right);
        }

        return root;
    }
};

Complexity Analysis:

• Time Complexity:O(n)
• Space Complexity:O(w)
  • w is the maximum width of the tree, in the worst case it could be O(n)

3️⃣ Iterative Approach (Using Stack - DFS)

Intuition:

Use a stack to perform a DFS traversal. At each node, swap left and right children.

Approach:

1. Use a stack to simulate DFS.
2. At each node, swap the children.
3. Push non-null children into the stack.

Code:

#include <stack>
class Solution {
public:
    TreeNode* invertTree(TreeNode* root) {
        if (root == nullptr) return nullptr;

        std::stack<TreeNode*> st;
        st.push(root);

        while (!st.empty()) {
            TreeNode* current = st.top();
            st.pop();

            // Swap children
            swap(current->left, current->right);

            if (current->left) st.push(current->left);
            if (current->right) st.push(current->right);
        }

        return root;
    }
};

Complexity Analysis:

• Time Complexity:O(n)
• Space Complexity:O(h)
  • h is the height of the tree (stack size in DFS). Worst case: O(n)