Problem Statement
Given an array nums of size n and an integer k, find the length of the longest sub-array that sums up to k. If no such sub-array exists, return 0.
Examples
Example 1:
Input: nums = [10, 5, 2, 7, 1, 9], k = 15
Output: 4
Explanation: The longest sub-array with a sum equal to 15 is [5, 2, 7, 1], which has a length of 4. This sub-array starts at index 1 and ends at index 4, and the sum of its elements (5 + 2 + 7 + 1) equals 15. Therefore, the length of this sub-array is 4.Example 2:
Input: nums = [-3, 2, 1], k = 6
Output: 0
Explanation: There is no sub-array in the array that sums to 6. Therefore, the output is 0.Different Approaches
1️⃣ Brute Force Approach
Intuition:
The brute force approach checks every possible subarray and calculates its sum. If the sum equals k, it calculates the length of that subarray and updates the maximum length if needed.
Dry Run:
Input:
nums = [1, 2, 3, 2, 1, 5], k = 5
Execution:
- Initialize
maxLength = 0.
| i | j | Subarray | Sum | Length | maxLength |
|---|---|---|---|---|---|
| 0 | 0 | [1] | 1 | - | 0 |
| 0 | 1 | [1, 2] | 3 | - | 0 |
| 0 | 2 | [1, 2, 3] | 6 | - | 0 |
| 0 | 3 | [1, 2, 3, 2] | 8 | - | 0 |
| 0 | 4 | [1, 2, 3, 2, 1] | 9 | - | 0 |
| 0 | 5 | [1, 2, 3, 2, 1, 5] | 14 | - | 0 |
| 1 | 1 | [2] | 2 | - | 0 |
| 1 | 2 | [2, 3] | 5 | 2 | 2 |
| 1 | 3 | [2, 3, 2] | 7 | - | 2 |
| 1 | 4 | [2, 3, 2, 1] | 8 | - | 2 |
| 1 | 5 | [2, 3, 2, 1, 5] | 13 | - | 2 |
| 2 | 2 | [3] | 3 | - | 2 |
| 2 | 3 | [3, 2] | 5 | 2 | 2 |
| 2 | 4 | [3, 2, 1] | 6 | - | 2 |
| 3 | 3 | [2] | 2 | - | 2 |
| 3 | 4 | [2, 1] | 3 | - | 2 |
| 3 | 5 | [2, 1, 5] | 8 | - | 2 |
| 4 | 4 | [1] | 1 | - | 2 |
| 4 | 5 | [1, 5] | 6 | - | 2 |
| 5 | 5 | [5] | 5 | 1 | 2 |
Output
maxLength = 2
Code:
class Solution {
public:
int longestSubarray(vector<int>& nums, int k) {
int maxLength = 0;
for (int i = 0; i < nums.size(); i++) {
int sum = 0; // Initialize sum for the current starting index
for (int j = i; j < nums.size(); j++) {
sum += nums[j]; // Add the current element to the sum
if (sum == k) {
int length = j - i + 1; // Calculate the subarray length
maxLength = max(maxLength, length); // Update maxLength
}
}
}
return maxLength;
}
};
Complexity Analysis:
- Time Complexity:
O(n^2)- Outer loop:
O(n) - Inner loop:
O(n) - Total =
O(n^2)
- Outer loop:
- Space Complexity:
O(1)- As no extra space is used.
2️⃣ Optimal Approach
Intuition:
In this approach, we use the concept of prefix sums to solve the problem of finding the longest subarray with a sum equal to 𝑘. The prefix sum of a subarray ending at index 𝑖 is simply the sum of all the elements of that subarray. By keeping track of these prefix sums and their occurrences, we can efficiently determine the longest subarray that meets the criteria.
Approach:
- First, we will declare a map to store the prefix sums and their corresponding indices.
- We will run a loop from index 0 to n-1 (where n is the size of the array).
- For each index i, add the current element a[i] to the prefix sum. If the prefix sum equals k, consider the length of the current subarray (i+1) and update the maximum length if needed. Calculate the prefix sum for the remaining subarray (prefix sum - k).
- If this remaining sum exists in the map, calculate the length of the subarray ending at i and starting after the prefix sum, i.e., i - map[remaining sum], and update the maximum length if this length is greater. If the remaining sum does not exist in the map, add the current prefix sum and index to the map to ensure we store the earliest index where each prefix sum occurs.
- The prefix sum of a subarray ending at index i is simply the sum of all the elements up to that index. By tracking these sums and their occurrences, we can efficiently determine the longest subarray that sums to k.
Observations:
Assume the prefix sum of a subarray ending at index i is x. We need to find another subarray ending at i whose sum equals k. If such a subarray exists, the prefix sum of the remaining part will be x-k.
For a subarray ending at index i with the prefix sum x, if we remove the part with the prefix sum x-k, we are left with a subarray whose sum equals k. This is our target.
Instead of searching for subarrays with sum k, we will use a map to track the prefix sums at each index. The map will store each prefix sum and its corresponding index as a key-value pair. At index i, we will check the map for the prefix sum x-k. If it exists, we calculate the subarray length as i - preSumMap[x-k]. We update the maximum length if this subarray is longer.
We repeat this process for all indices from 0 to n-1 (where n is the size of the array).
Edge Case:
Why do we need to check if the prefix sum already exists in the map? Let's understand with an example:
Assume the array is [2, 0, 0, 3] and k = 3. If we don't check the map before inserting, the algorithm might incorrectly update the index for repeated prefix sums. For instance, at indices 2 and 3, the prefix sum remains the same but the index is updated. When i reaches the end, the calculated length might be incorrect. To avoid this, we only update the map with the first occurrence of each prefix sum. This ensures we get the maximum subarray length. Take the reference of the below image for better understanding.
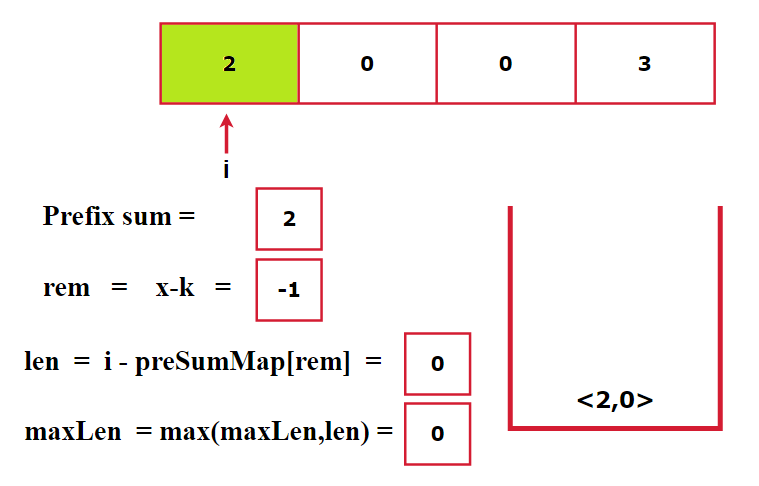
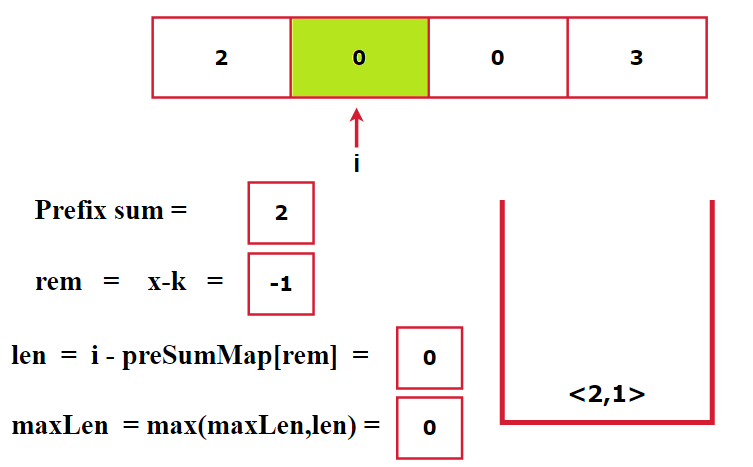


Approach:
- Initialize:
- Use a hash map (
prefixSumMap) to store the first occurrence of a prefix sum. - Start with
prefixSum = 0andmaxLen = 0.
- Use a hash map (
- Iterate through the array:
- Add the current element to
prefixSum. - Check if
prefixSum == K. If true, updatemaxLenwith the current index + 1. - Check if
(prefixSum - K)exists in the hash map:- If it exists, calculate the length of the subarray as
current_index - prefixSumMap[prefixSum - K]. - Update
maxLenif the calculated length is greater.
- If it exists, calculate the length of the subarray as
- If
prefixSumis not already in the hash map, store its index.
- Add the current element to
- Return
maxLen:- This contains the length of the longest subarray with sum
K.
- This contains the length of the longest subarray with sum
Code:
class Solution
{
public:
int longestSubarray(vector<int> &nums, int k)
{
int n = nums.size();
map<int, int> preSumMap;
int sum = 0;
int maxLen = 0;
for (int i = 0; i < n; i++) {
// calculate the prefix sum till index i
sum += nums[i];
// if the sum equals k, update maxLen,
// this is for the case when entire subarray encountered so far is equal to target
if (sum == k) {
maxLen = max(maxLen, i + 1);
}
// calculate the sum of remaining part i.e., sum - k
int rem = sum - k;
// calculate the length and update maxLen
if (preSumMap.find(rem) != preSumMap.end()) {
int len = i - preSumMap[rem];
maxLen = max(maxLen, len);
}
// update the map if sum is not already present
if (preSumMap.find(sum) == preSumMap.end()) {
preSumMap[sum] = i;
}
}
return maxLen;
}
};Complexity Analysis:
- Time Complexity:
O(N)orO(NxlogN)depending on the map data structure used, where N is the size of the array. For example, using an unordered_map in C++ gives a time complexity of O(N) (though in the worst case, unordered_map takes O(N) to find an element, making the time complexity O(N^2)). If we use a map data structure, the time complexity is O(NxlogN). The best case complexity is O(N) as we are traversing the array with a loop. - Space Complexity:
O(N), since we are using a map data structure
