Problem Statement

Given a string, Find the longest palindromic subsequence length in given string.

A palindrome is a sequence that reads the same backwards as forward.

A subsequence is a sequence that can be derived from another sequence by deleting some or no elements without changing the order of the remaining elements.

Examples

Example 1:

Input: s = "eeeme"
Output: 4

Explanation: The longest palindromic subsequence is "eeee", which is of length 4.

Example 2:

Input: s = "annb"
Output: 2

Explanation: The longest palindromic subsequence is "nn", which is of length 2.

Different Approaches

1️⃣ Recursive Approach

class Solution {
public:
    // Recursive function to find the Longest Palindromic Subsequence
    int helper(string& s, int i, int j) {
        // Base case: If the indices cross, return 0 (empty substring)
        if (i > j) {
            return 0;
        }

        // Base case: If only one character is left, it's a palindrome of length 1
        if (i == j) {
            return 1;
        }

        // If characters match, they contribute to the palindromic subsequence
        if (s[i] == s[j]) {
            return 2 + helper(s, i + 1, j - 1);  // Include both characters
        } else {
            // Otherwise, we try both possibilities (skipping one character at a time)
            return max(helper(s, i + 1, j), helper(s, i, j - 1));
        }
    }

    // Public function to calculate the longest palindromic subsequence
    int longestPalindromeSubseq(string s) {
        return helper(s, 0, s.size() - 1);  // Start recursion from the full string
    }
};

Complexity Analysis:

• Time Complexity: O(2 ^ n), where n is the length of the string.
• Space Complexity: O(n), due to the recursion.

2️⃣ Memoization

We are given a string S, the simplest approach will be to generate all the subsequences and store them, then manually find out the longest palindromic subsequence. This naive approach will give us the correct answer but to generate all the subsequences, we will require exponential ( 2n ) time. Therefore we will try some other approaches.

Using Dynamic Programming:

We can use the approach discussed in the article Longest Common Subsequence, to find the Longest Palindromic Subsequence.

Understanding:

Let us say that we are given the following string:

The longest palindromic subsequence will be: “babcbab”. The special thing about this string is that it is palindromic (equal to its reverse) and of the longest length.

Now let us write the reverse of 'str' next to it and focus on the highlighted characters. If we look closely at the highlighted characters, they are nothing but the longest common subsequence of the two strings.

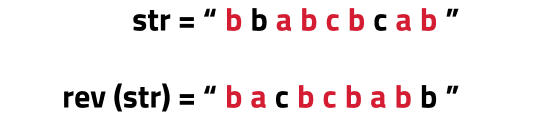
Now, we have taken the reverse of the string for the following two reasons:

• The longest palindromic subsequence being a palindrome will remain the same when the entire string is reversed.
• The length of the palindromic subsequence will also remain the same when the entire string is reversed.

From the above discussion we can conclude that the longest palindromic subsequence of a string is the longest common subsequence of the given string and its reverse.

Approach:

1. We are given a string (say s), make a copy of it and store it( say string t).
2. Reverse the original string s.
3. Find the longest common subsequence as discussed in Longest Common Subsequence.

Code:

class Solution {
public:
    // Helper function with memoization
    int helper(string& s, int i, int j, vector<vector<int>>& dp) {
        // Base case: if indices cross, return 0 (empty substring)
        if (i > j) {
            return 0;
        }

        // Base case: single character is a palindrome of length 1
        if (i == j) {
            return 1;
        }

        // If already computed, return the stored result
        if (dp[i][j] != -1) {
            return dp[i][j];
        }

        // If characters match, include both in the subsequence
        if (s[i] == s[j]) {
            dp[i][j] = 2 + helper(s, i + 1, j - 1, dp);
        } else {
            // Otherwise, take the maximum by skipping one character at a time
            dp[i][j] = max(helper(s, i + 1, j, dp), helper(s, i, j - 1, dp));
        }

        return dp[i][j];
    }

    // Public function to calculate the longest palindromic subsequence
    int longestPalindromeSubseq(string s) {
        int n = s.size();
        
        // Initialize DP table with -1
        vector<vector<int>> dp(n, vector<int>(n, -1));
        
        // Start the recursive function with the full range of the string
        return helper(s, 0, n - 1, dp);
    }
};

Complexity Analysis:

• Time Complexity: O(N*N), Where N is the length of the given string. Two nested loops are used in order to solve this problem.
• Space Complexity: O(N*N), We are using an external array of size ‘(N*N)’.

3️⃣ Space Optimization

If we observe the relations obtained in tabultaion approach, dp[ind1 - 1][ind2], dp[ind1][ind2 - 1]. We are using just two rows, dp[ind1-1][ ], dp[ind][ ], in order to calculate the present row.

So we are not required to contain an entire array, we can simply have two rows 'prev' and 'cur' where prev corresponds to dp[ind-1] and cur to dp[ind].

After declaring 'prev' and 'cur', replace dp[ind-1] to prev and dp[ind] with cur in the tabulation code. Following the same logic of tabulation, we will calculate cur[ind] in each iteration and after the inner loop executes, we will set prev = cur, so that the cur row can serve as prev for the next index.

After end of the execution, return prev[n] (n is the length of the string), as our answer, as it will hold the cumulative result of the overall calculation.

Code:

#include <bits/stdc++.h>
using namespace std;

class Solution{
private:
    /* Function to calculate the length of 
    the Longest Palindromic Subsequence*/
    int lcs(string s1, string s2) {
        int n = s1.size();
        int m = s2.size();

        /* Create two arrays to store the 
        previous and current rows of DP values*/
        vector<int> prev(m + 1, 0), cur(m + 1, 0);

        /* Base Case is covered as we have
        initialized the prev and cur to 0.*/

        for (int ind1 = 1; ind1 <= n; ind1++) {
            for (int ind2 = 1; ind2 <= m; ind2++) {
                if (s1[ind1 - 1] == s2[ind2 - 1])
                    cur[ind2] = 1 + prev[ind2 - 1];
                else
                    cur[ind2] = max(prev[ind2], cur[ind2 - 1]);
            }
            // Update the prev array with current values
            prev = cur;
        }
        // The value at prev[m] contains length of LCS
        return prev[m];
    }
public:
    /* Function to calculate the length of 
    the Longest Palindromic Subsequence*/
    int longestPalinSubseq(string s){
        // Store a reversed copy of the string
        string t = s;
        reverse(s.begin(), s.end());

        /* Call the LCS function to find the 
        length of the Longest Common Subsequence*/
        return lcs(s, t);
    }
};
int main() {
    string s = "bbabcbcab";
    
    //Create an instance of Solution class
    Solution sol;
    
    // Print the result
    cout << "The Length of Longest Palindromic Subsequence is " << sol.longestPalinSubseq(s);
    return 0;
}

Complexity Analysis:

• Time Complexity: O(N*N), Where N is the length of the given string. Two nested loops are used in order to solve this problem.
• Space Complexity: O(N), We are using an external array of size ‘N+1’ to store only two rows.