Problem Statement

Given a wooden stick of length n units. The stick is labelled from 0 to n. Given an integer array cuts where cuts[i] denotes a position you should perform a cut at. Perform the cuts in any order, you can change the order of the cuts as you wish.

The cost of one cut is the length of the stick to be cut, the total cost is the sum of costs of all cuts. When a stick is cut, it will be split into two smaller sticks (i.e. the sum of their lengths is the length of the stick before the cut). Return the minimum total cost of the cuts.

Examples

Example 1:

Input: n = 7, cuts = [1, 3, 4, 5]
Output: 16

Explanation: Using cuts order = [1, 3, 4, 5] as in the input leads to the following scenario:

The first cut is done to a rod of length 7 so the cost is 7. The second cut is done to a rod of length 6 (i.e. the second part of the first cut), the third is done to a rod of length 4 and the last cut is to a rod of length 3. The total cost is 7 + 6 + 4 + 3 = 20.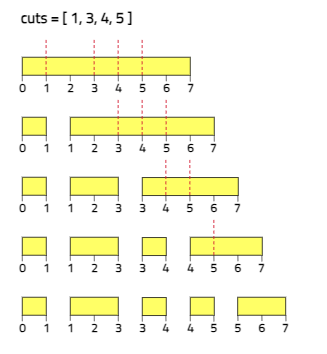

Rearranging the cuts to be [3, 5, 1, 4] for example will lead to a scenario with total cost = 16 (as shown in the example photo 7 + 4 + 3 + 2 = 16).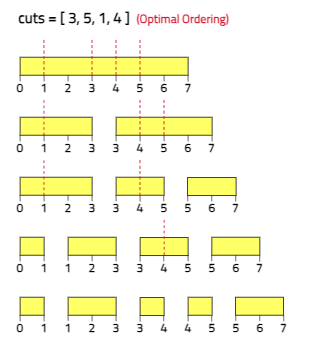

Example 2:

Input: n = 7, cuts = [1, 3, 6]
Output: 14

Explanation: The optimal order for cutting the stick is [3, 1, 6].
The cost will be => 7 + 3 + 4 => 14.

Different Approaches

1️⃣ Recursive Approach

We need to minimize the cost incurred to cut the stick. Whenever we make a cut, we are changing the length of the stick which in turn decides the cost. Therefore the order in which we make the cuts changes the total cost. As discussed in previous problem, whenever the order of solving the problem comes into play, we can think in terms of Partition DP.

Rules to solve a problem on partition dp:

• Marking the array with i,j: We are given a stick of size N and the CUTS array. Every element of the CUTS array represents the marking at which one cut needs to be made. When we make a cut, we are dividing the stick into two different parts.
  • Ideally, we would want to place the i, and j pointers at both ends of the CUTS array and try to solve the problem recursively, which we will eventually do. But we need to modify the given array. We will first discuss the need for a modification and then we will learn about the exact modification required. We have the following example:

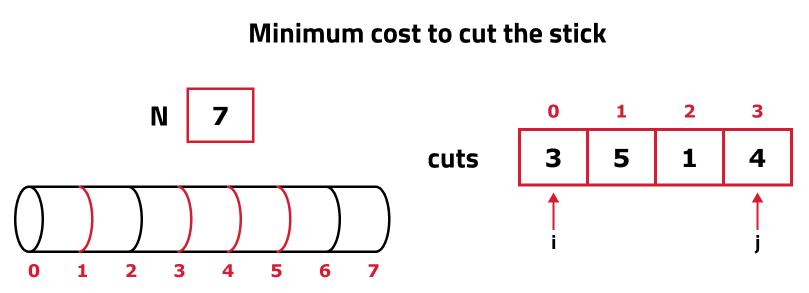
Now, we try to place i and j on both ends of the CUTS array. Suppose we want to cut the stick at CUTS[0], i.e marking 3, then we will divide the bigger problem ( stick of length 7) into two smaller problems ( sticks of length 3 and 4) and solve these sub-problems independently (as we are looking for a recursive solution). Now the problem which arises is that when we make a cut at marking 3, we also need to think of something to distribute the CUTS array. This means we need to define separate i, and j pointers for each subproblem. We can try breaking the CUTS array in the following way:

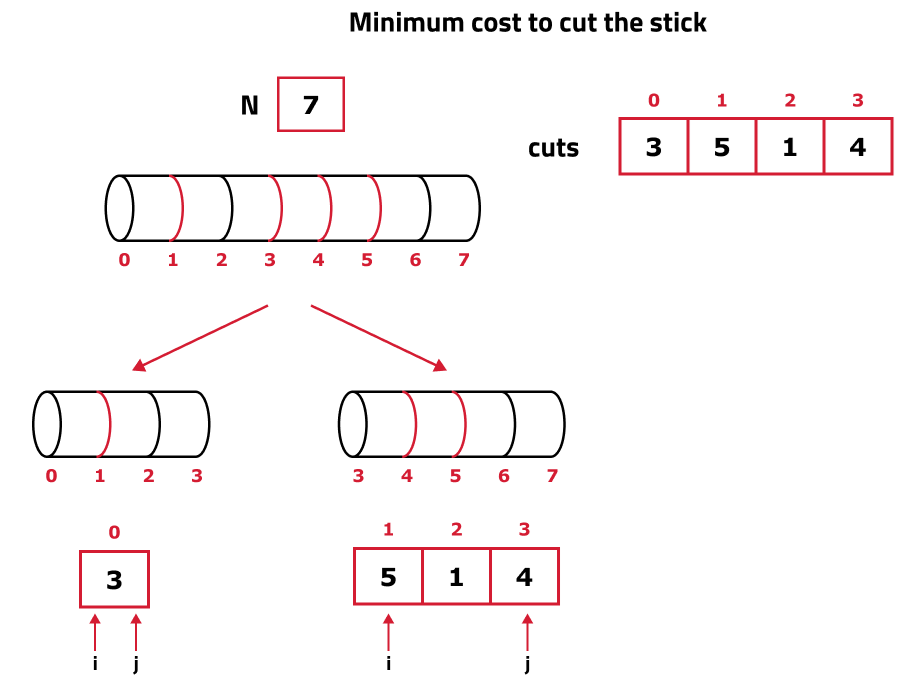
• Try out all Partitions: As we have figured out the logic for marking the i, and j pointers, we will move to the partitioning loop. We can simply write a for loop(say ind) starting from i to j, The problem is being broken in the following manner:

/*It is a pseudocode and it not tied to
any specific programming language*/

f(i, j){
    for(int ind = i; ind <= j; ind++){
        ans = cuts[j+1] - cuts[i-1] + f(i, ind-1, cuts) + f(ind+1, j, cuts)
    }
}

Note: We are breaking the left subproblem to f(i,ind-1) rather than f(i,ind) because we have already made a cut at CUTS[ind] and we don't want to consider it twice.

• Base Case: As i <=j, we can say that when i>j this is not a valid partition so we can return 0.
• Return the best possible answer to the two partitions: We know that the recursive functions along with the base case will get us the answer to the subproblems, but still, there is some work to do. We need to find the cost incurred to make the cut that is breaking the stick at CUTS[ind]. The cost incurred will be the length of the stick on which the cut is being made. We only have the CUTS array to figure it out, let's see how.

If we push 0 and N to both ends of the CUTS array:

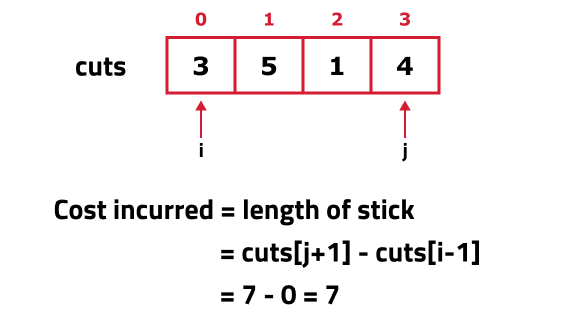
Then CUTS[j+1] - CUTS[i-1] will always give us the correct length of the stick on which the cut is being made. Readers are advised to dry run with some other examples too to understand this.

/*It is a pseudocode and it not tied to
any specific programming language*/

f(i, j){
    mini = INT_MAX
    for(int ind = i; ind <= j; ind++){
        ans = cuts[j+1] - cuts[i-1] + f(i, ind-1, cuts) + f(ind+1, j, cuts)
        mini = min(mini, ans)
    }
}

To summarize:

1. Sort the CUTS array.
2. Append 0 and N at both ends of the CUTS array.
3. Convert the problem to a recursive function marked by two pointers i and j.
4. Use a partitioning loop to try all partitions.
5. Return the answer in which the partition gives the minimum cost.

Code:

#include <bits/stdc++.h>
using namespace std;

class Solution{
private:
    // Function to calculate the minimum cost incurred
    int func(int i, int j, vector<int> &cuts) {
        /* Base case: If i is greater than 
        j, there are no cuts to consider.*/
        if (i > j) {
            return 0;
        }
        
        int mini = INT_MAX;

        for (int ind = i; ind <= j; ind++) {
            /* Calculate the cost for
            making a cut at position 'ind'.*/
            int ans = cuts[j + 1] - cuts[i - 1] + func(i, ind - 1, cuts) + func(ind + 1, j, cuts);

            mini = min(mini, ans);
        }
        //Return the result
        return mini;
    }
public:
    // Function to compute the minimum cost
    int minCost(int n, vector<int> &cuts) {
        int c = cuts.size();
        /* Modify the cuts array by adding 0 
        at the beginning and 'n' at the end.*/
        cuts.push_back(n);
        cuts.insert(cuts.begin(), 0);
        sort(cuts.begin(), cuts.end());

       // Call the recursive function to find minimum cost.
       return func(1, c, cuts);
    }
};

int main() {
    vector<int> cuts = {3, 5, 1, 4};
    int n = 7;
    
    //Create an instance of Solution class
    Solution sol;
    
    cout << "The minimum cost incurred is: " << sol.minCost(n, cuts) << endl;

    return 0;
}

Complexity Analysis:

• Time Complexity: Exponential.
• Space Complexity: O(N), We are using an auxiliary recursion stack space O(N).

2️⃣ Memoization

If we draw the recursion tree, we will see that there are overlapping subproblems. Hence the DP approaches can be applied to the recursive solution.

In order to convert a recursive solution to memoization the following steps will be taken:

• Declare a dp array of size [c+1][c+1]: As there are two changing parameters in the recursive solution, 'i' and 'j'. The value of 'i' and 'j' ranges from 0 to c. Therefore, we need 2D dp array.
  • The dp array stores the calculations of subproblems. Initialize dp array with -1, to indicate that no subproblem has been solved yet.
• While encountering an overlapping subproblem: When we come across a subproblem, for which the dp array has value other than -1, it means we have found a subproblem which has been solved before hence it is an overlapping subproblem. No need to calculate it's value again just retrieve the value from dp array and return it.
• Store the value of subproblem: Whenever, a subproblem is encountered and it is not solved yet(the value at this index will be -1 in the dp array), store the calculated value of subproblem in the array.

Code:

#include <bits/stdc++.h>
using namespace std;

class Solution{
private:
    // Function to calculate the minimum cost incurred
    int func(int i, int j, vector<int> &cuts, vector<vector<int>> &dp) {
        /* Base case: If i is greater than 
        j, there are no cuts to consider.*/
        if (i > j) {
            return 0;
        }
        
        //Check if the subproblem is already solved
        if (dp[i][j] != -1) {
            return dp[i][j];
        }
        
        int mini = INT_MAX;

        for (int ind = i; ind <= j; ind++) {
            /* Calculate the cost for
            making a cut at position 'ind'.*/
            int ans = cuts[j + 1] - cuts[i - 1] + func(i, ind - 1, cuts, dp) + func(ind + 1, j, cuts, dp);

            mini = min(mini, ans);
        }
        //Return the result
        return dp[i][j] = mini;
    }
public:
    // Function to compute the minimum cost
    int minCost(int n, vector<int> &cuts) {
        int c = cuts.size();
        /* Modify the cuts array by adding 0 
        at the beginning and 'n' at the end.*/
        cuts.push_back(n);
        cuts.insert(cuts.begin(), 0);
        sort(cuts.begin(), cuts.end());
        
        // Create a DP table to store calculated values.
        vector<vector<int>> dp(c + 1, vector<int>(c + 1, -1));

       // Call the recursive function to find minimum cost.
       return func(1, c, cuts, dp);
    }
};

int main() {
    vector<int> cuts = {3, 5, 1, 4};
    int n = 7;
    
    //Create an instance of Solution class
    Solution sol;
    
    cout << "The minimum cost incurred is: " << sol.minCost(n, cuts) << endl;

    return 0;
}

Complexity Analysis:

• Time Complexity: O(N*N*N), There are N*N states and we explicitly run a loop inside the function which will run for N times, therefore at max ‘N*N*N’ new problems will be solved.
• Space Complexity: O(N*N) + O(N). We are using an auxiliary recursion stack space O(N) and a 2D array O(N*N).