Problem Statement
Given an undirected graph with V vertices labeled from 0 to V-1. The graph is represented using an adjacency list where adj[i] lists all nodes connected to node. Determine if the graph is bipartite or not.
A graph is bipartite if the nodes can be partitioned into two independent sets A and B such that every edge in the graph connects a node in set A and a node in set B.
Equivalent, a graph is bipartite if it is 2-colorable, you can color all vertices using two colors such that no two adjacent vertices share the same color.
Examples
Example 1:
Input: V = 4,
adj = [
[1, 3],
[0, 2],
[1, 3],
[0, 2]
]
0 --- 1
| |
3 --- 2
Output: true
Explanation:
The given graph is bipartite since, we can partition the nodes into two sets: {0, 2} and {1, 3}.Example 2:
Input: V = 3,
adj = [
[1, 2],
[0, 2],
[0, 1]
]
0
/ \
1---2
Output: false
Explanation:
No way to divide the vertices into two sets without edges within the same set. The graph is not bipartite.Different Approaches
1️⃣ BFS
Intuition:
A bipartite graph is a graph that can be colored using 2 colors such that no adjacent nodes have the same color. Any linear graph with no cycle is always a bipartite graph. With a cycle, any graph with an even cycle length can also be a bipartite graph. So, any graph with an odd cycle length can never be a bipartite graph.
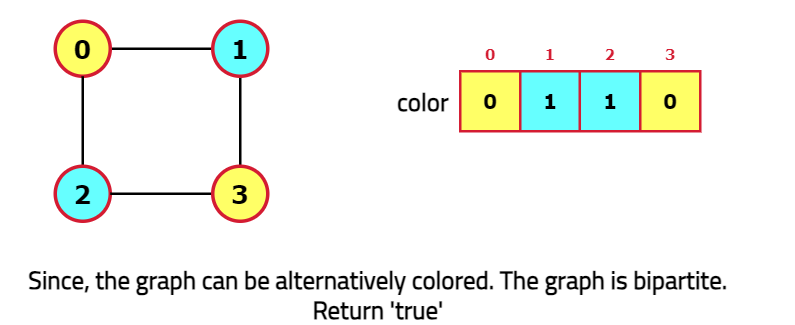
To check if the graph is bipartite, it can check if the nodes can be colored alternatingly. If alternate coloring of nodes is possible, the graph is bipartite, else not.
Approach:
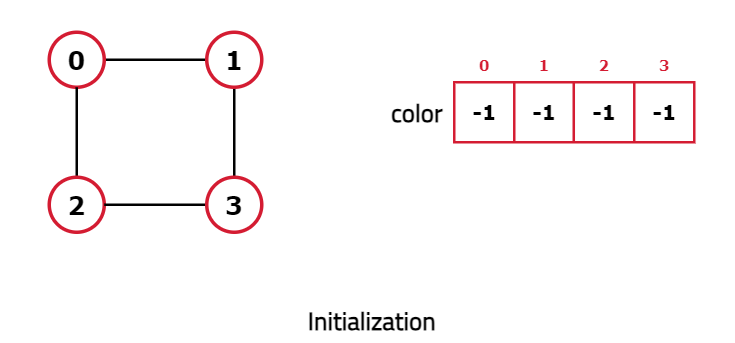
- Initialize a color array with all nodes initially uncolored represented by -1. Green and Yellow colors will be represented as integer value 0 and 1 respectively.
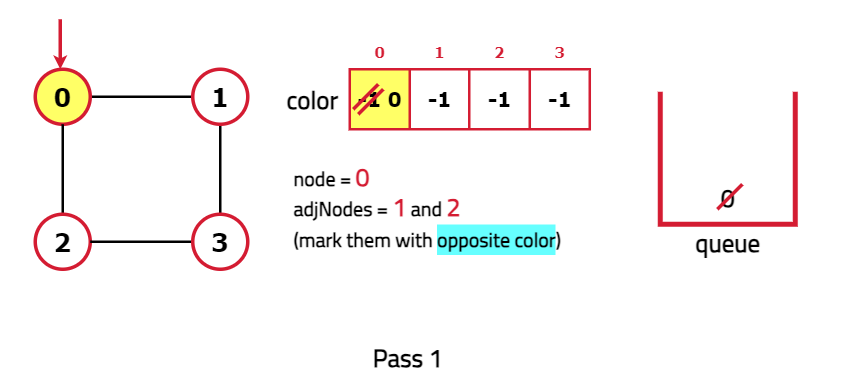
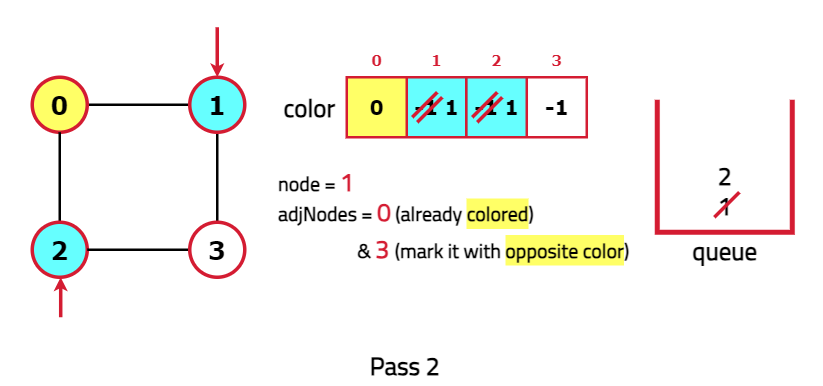
- Start the BFS traversal from an unvisited node and perform the following steps:
- If a node is uncolored, color it with alternating colors.
- If a node is previously colored, check if it follows alternate colors. If not, the graph can be said as not bipartite.
- If all the nodes can be colored with alternating colors, the graph can be classified as bipartite.
Dry Run:
Code:
#include <bits/stdc++.h>
using namespace std;
class Solution {
private:
/* Function to perform BFS traversal and color
the nodes with alternate colors in a component */
bool bfs(int start, int V, vector<int> adj[], int color[]) {
// Queue for BFS traversal
queue <int> q;
// Add initial node to queue
q.push(start);
color[start] = 0; // Mark it with a color
// While queue is not empty
while(!q.empty()) {
// Get the node
int node = q.front();
q.pop();
// Traverse all its neighbors
for(auto it : adj[node]) {
// If not already colored
if(color[it] == -1) {
// Color it with opposite color.
color[it] = !color[node];
// Push the node in queue
q.push(it);
}
// Else if the neighbor has same color as node
else if(color[it] == color[node]) {
/* Return false, as the
component is not bipartite */
return false;
}
}
}
// Return true is the component is bipartite
return true;
}
public:
/* Function to check if the
given graph is bipartite */
bool isBipartite(int V, vector<int> adj[]) {
/* To store the color of nodes, where
each node is uncolored initially */
int color[V];
for(int i=0; i < V; i++) color[i] = -1;
// Traverse all the nodes
for(int i=0; i < V; i++) {
// If not colored, start the traversal
if(color[i] == -1) {
// Return false if graph is not bipartite
if(!bfs(i, V, adj, color))
return false;
}
}
/* Return true if each
component is bipartite */
return true;
}
};
int main() {
int V = 4;
vector<int> adj[V] = {
{1,3},
{0,2},
{1,3},
{0,2}
};
/* Creating an instance of
Solution class */
Solution sol;
/* Function call to check
if the given graph is bipartite */
bool ans = sol.isBipartite(V, adj);
// Output
if(ans)
cout << "The given graph is a bipartite graph.";
else
cout << "The given graph is not a bipartite graph.";
return 0;
}Complexity Analysis:
- Time Complexity:
O(V+E)(where V is the number of nodes and E is the number of edges in the graph)
The BFS Traversal takesO(V+E)time. - Space Complexity:
O(V)
The color array takes O(V) space and queue space for BFS is O(V) for the worst case.
2️⃣ DFS
Intuition:
A bipartite graph is a graph that can be colored using 2 colors such that no adjacent nodes have the same color. Any linear graph with no cycle is always a bipartite graph. With a cycle, any graph with an even cycle length can also be a bipartite graph. So, any graph with an odd cycle length can never be a bipartite graph.
In order to check if the given graph is bipartite, it can checked if the nodes can be colors alternatingly. If alternate coloring of nodes is possible, the graph is bipartite, else not.
Approach:
- Initialize a color array with all nodes initially uncolored represented by -1. Green and Yellow colors will be represented as integer value 0 and 1 respectively.
- Start the DFS traversal from the node and perform the following steps:
- If a node is uncolored, color it with alternating colors.
- If a node is previously colored, check if it follows alternate colors. If not, the graph can be said as not bipartite.
- If all the nodes can be colored with alternating colors, the graph can be classified as bipartite.
Dry Run:
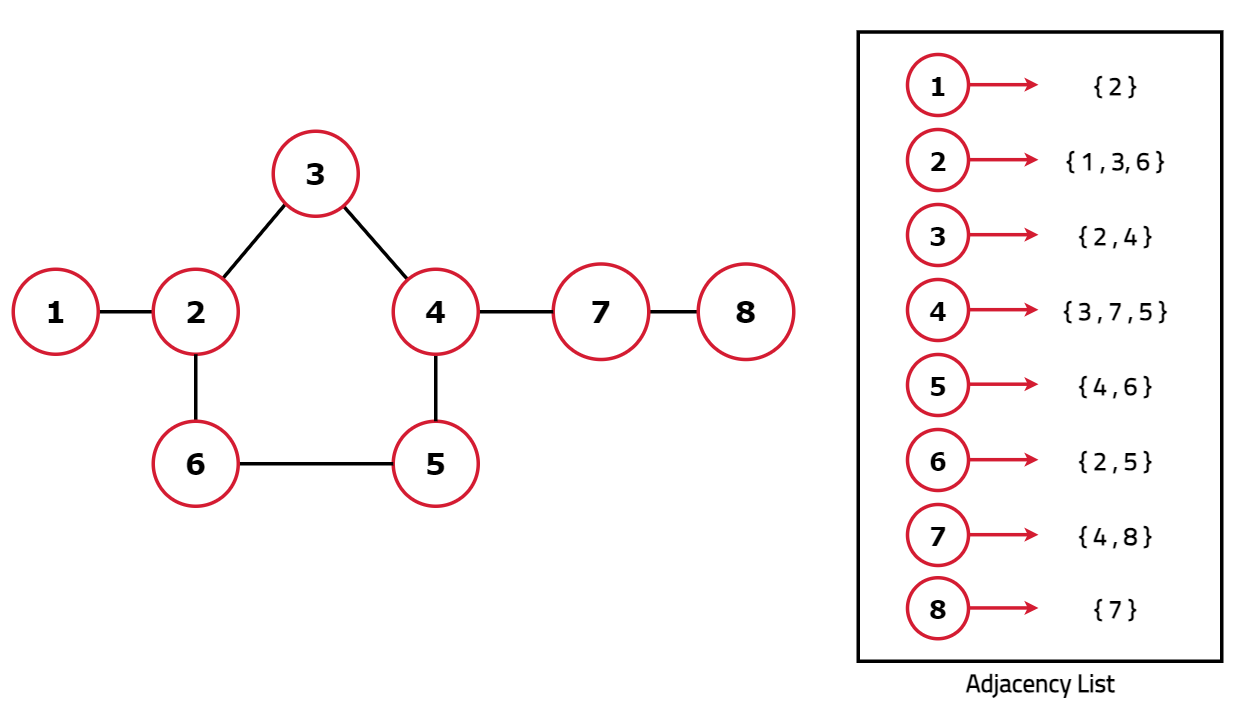
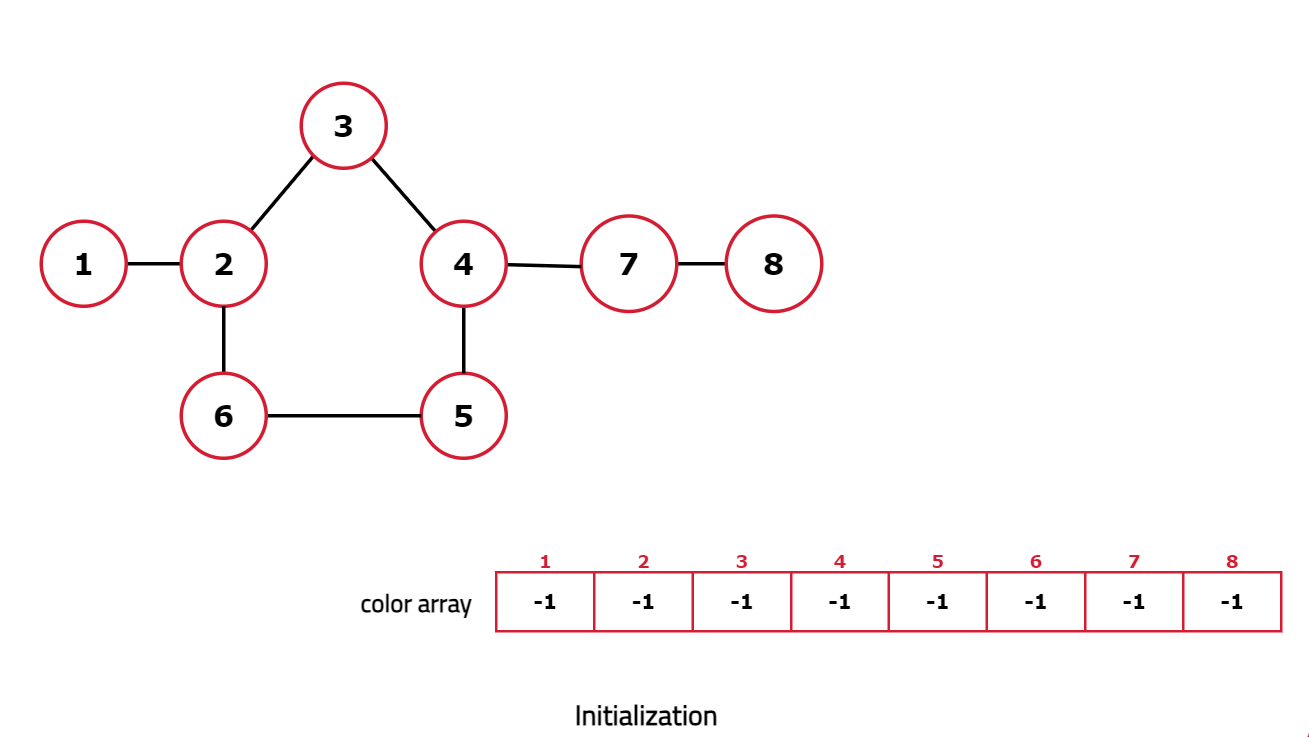
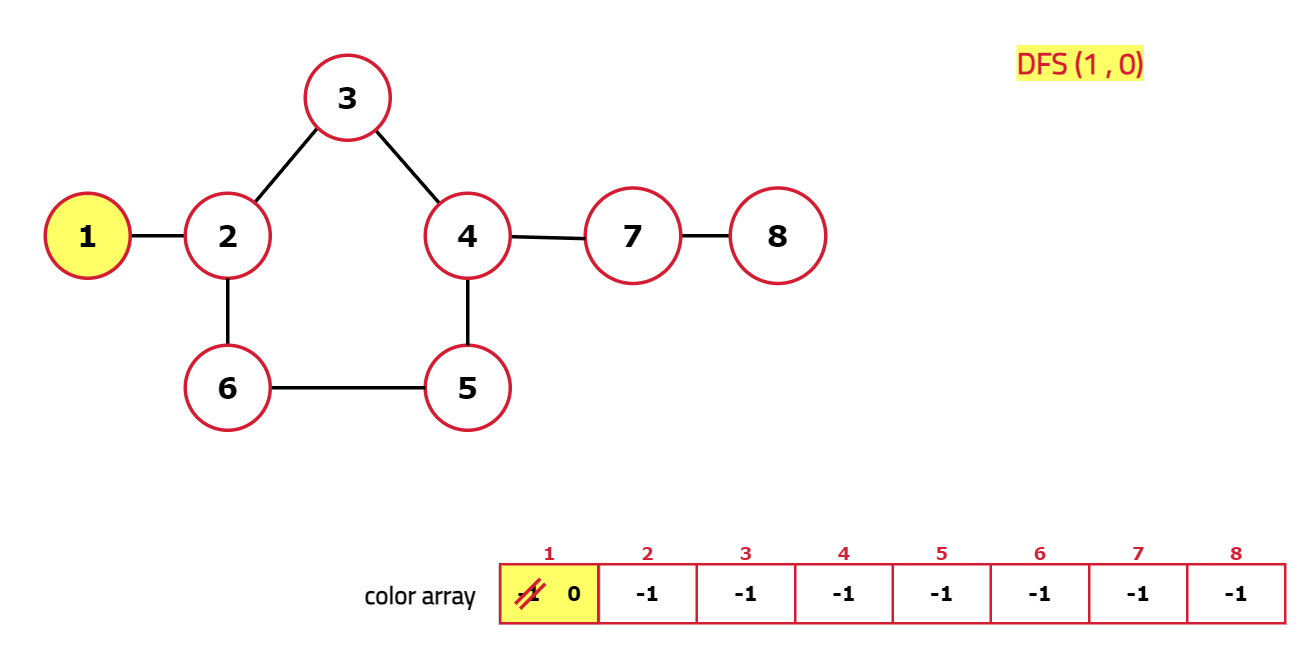
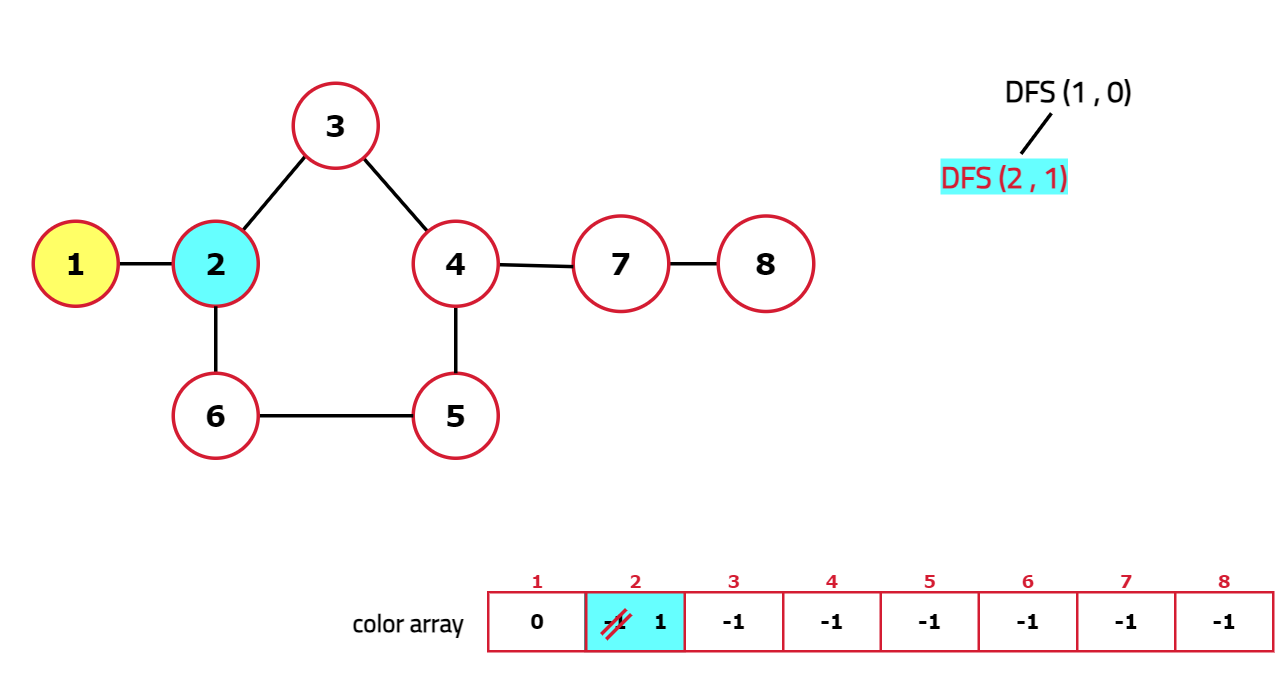
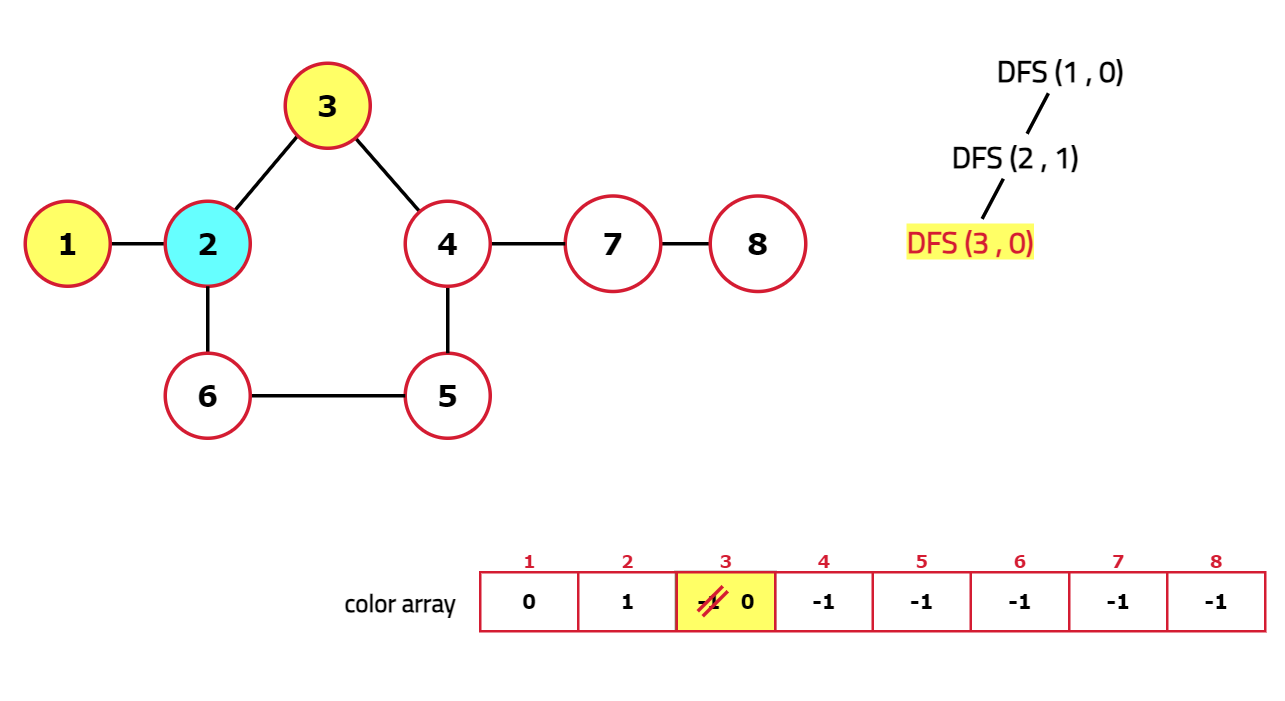
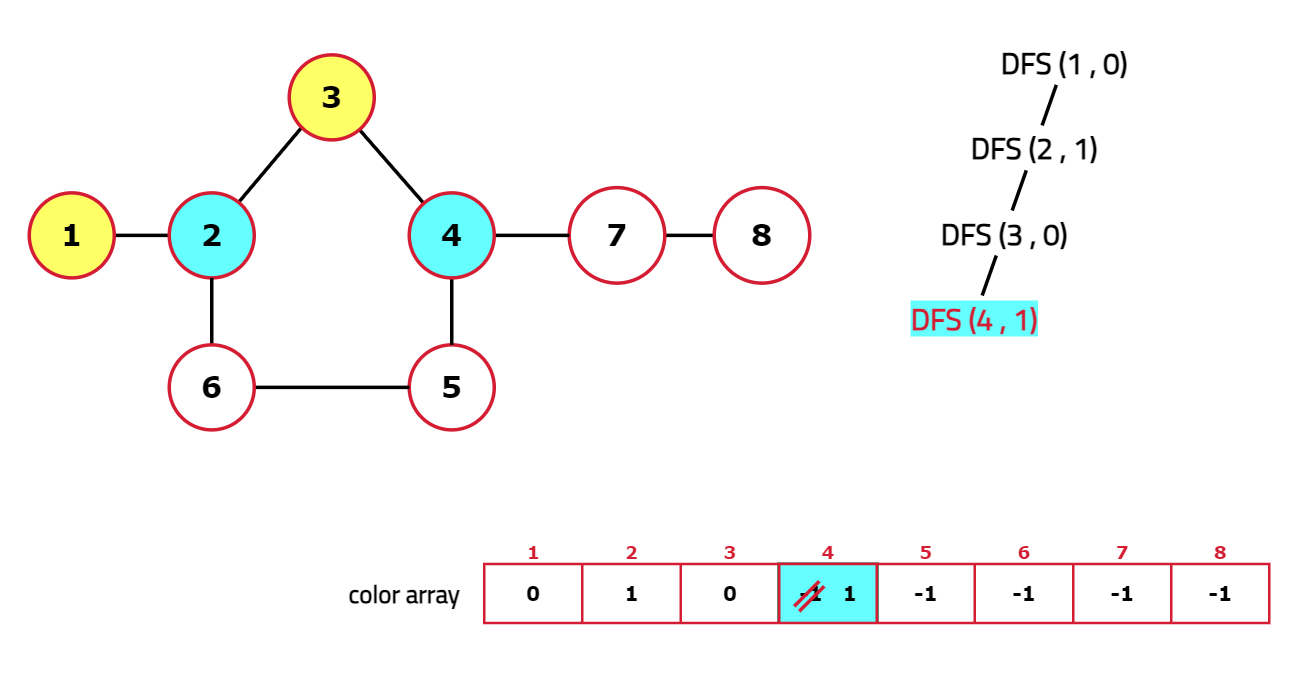
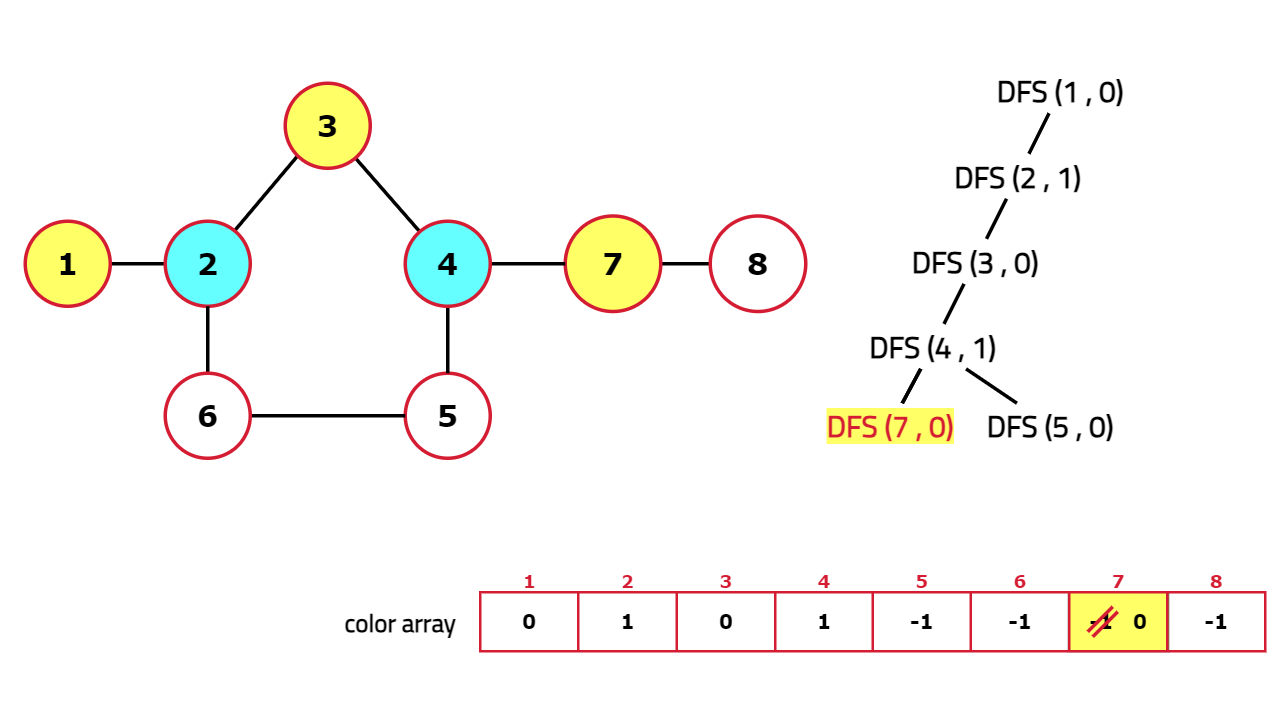
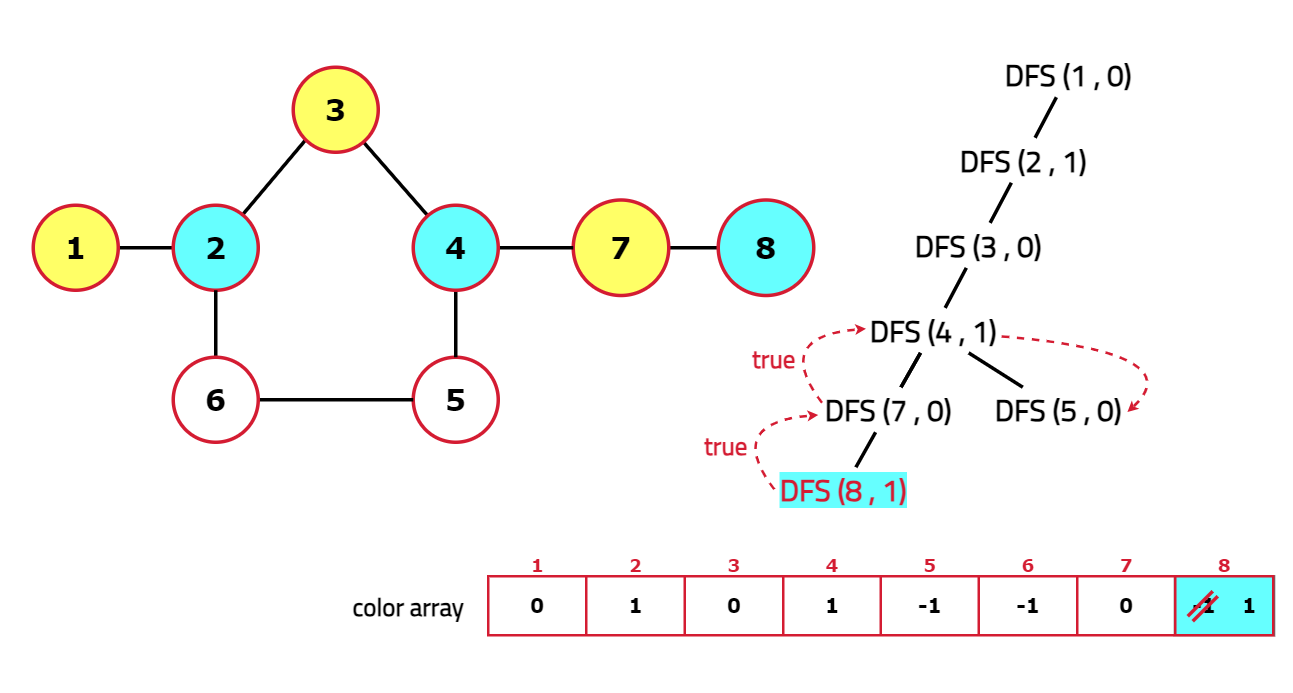
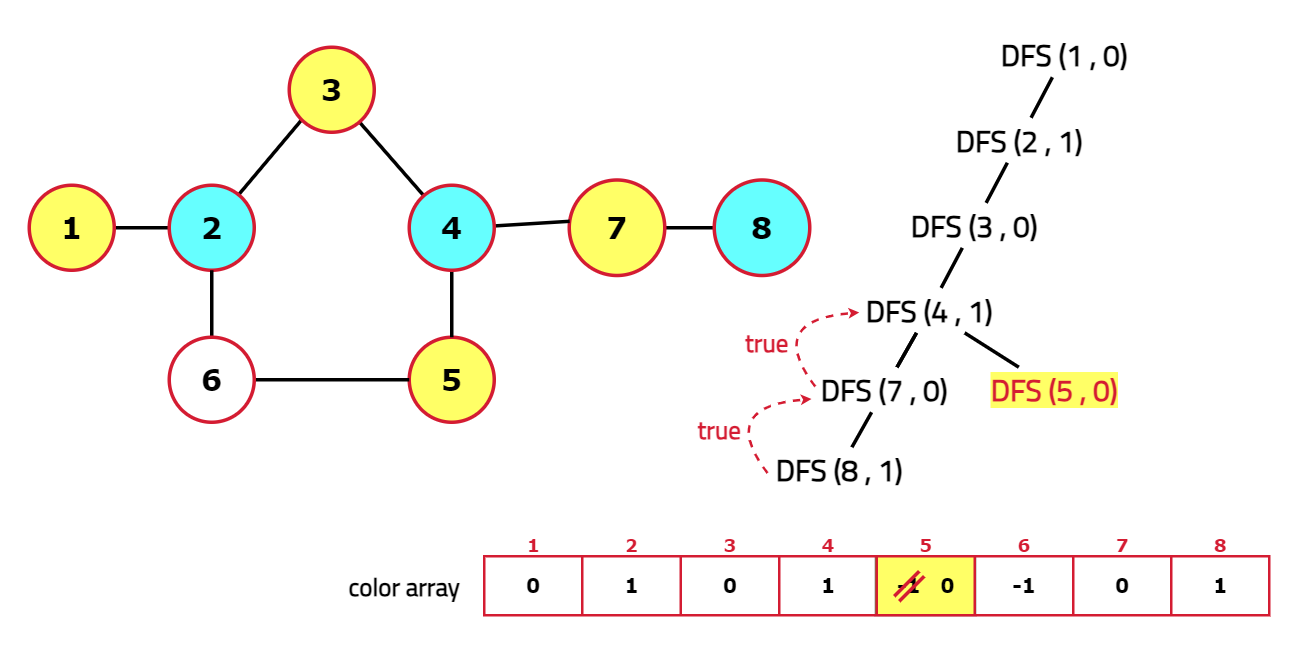
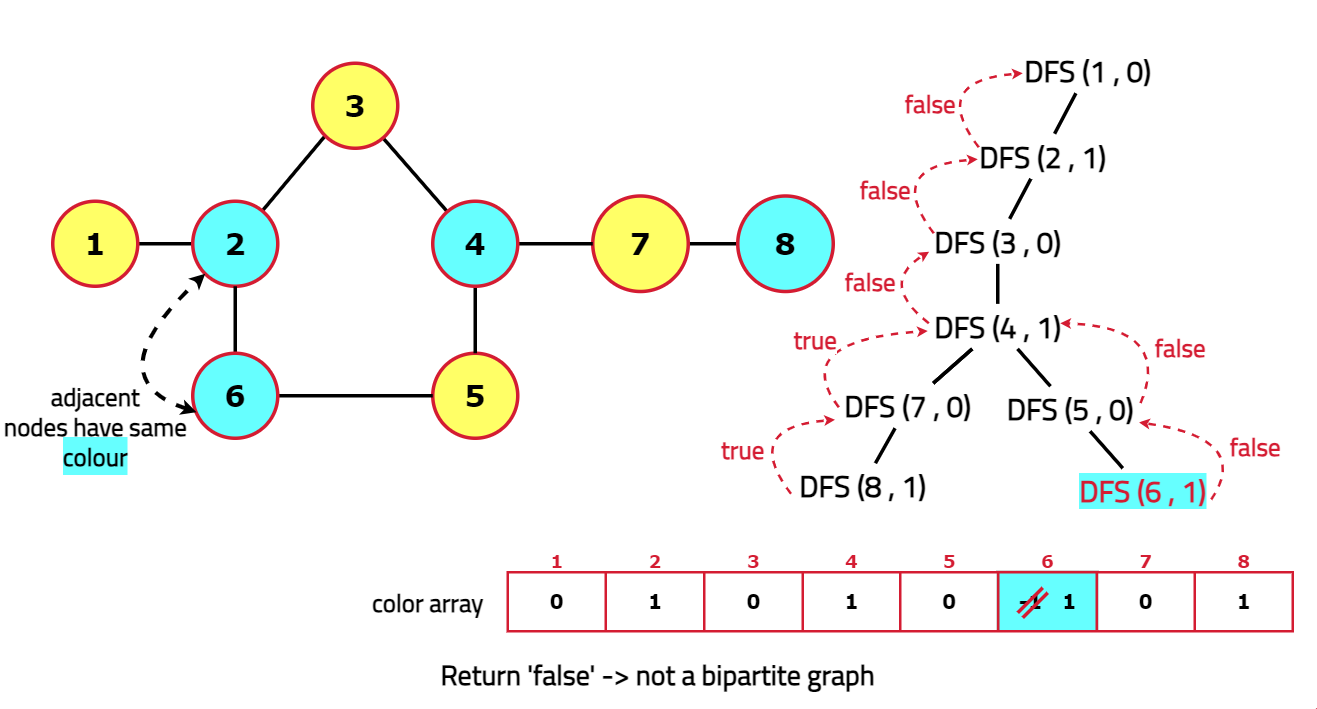
Code:
#include <bits/stdc++.h>
using namespace std;
class Solution {
private:
/* Function to perform DFS traversal and
color the nodes with alternate colors*/
bool dfs(int node, int col, vector<int> &color,
vector<int> adj[]) {
// Color the current node
color[node] = col;
// Traverse adjacent nodes
for(auto it : adj[node]) {
// if uncoloured
if(color[it] == -1) {
// Recursively color the nodes
if(dfs(it, !col, color, adj) == false)
return false;
}
// if previously coloured and have the same colour
else if(color[it] == col) {
// Return false as it is not bipartite
return false;
}
}
/* Return true if all the nodes can
be colored with alternate colors */
return true;
}
public:
/* Function to check if the
given graph is bipartite */
bool isBipartite(int V, vector<int> adj[]) {
/* To store the color of nodes, where
each node is uncolored initially */
vector<int> color(V, -1);
// Start Traversal of connected components
for(int i=0; i<V; i++) {
/* if a node is not colored,
a new component is found */
if(color[i] == -1) {
/* Start DFS traversal
and color each node */
if(dfs(i, 0, color, adj) == false) {
/* Return false if component
is found not to be bipartite */
return false;
}
}
}
/* Return true if each
component is bipartite */
return true;
}
};
int main() {
int V = 4;
vector<int> adj[V] = {
{1,3},
{0,2},
{1,3},
{0,2}
};
/* Creating an instance of
Solution class */
Solution sol;
/* Function call to check
if the given graph is bipartite */
bool ans = sol.isBipartite(V, adj);
// Output
if(ans)
cout << "The given graph is a bipartite graph.";
else
cout << "The given graph is not a bipartite graph.";
return 0;
}Complexity Analysis:
- Time Complexity: O(V+E) (where V is the number of nodes and E is the number of edges in the graph.)
The DFS Traversal takes O(V+E) time. - Space Complexity: O(V)
- The color array takes O(V) space and recursion stack space for DFS is O(V) for the worst case.
