Problem Statement

You are given two lists of closed intervals, firstList and secondList, where:

• firstList[i] = [starti, endi] represents the start and end of the i-th interval in firstList.
• secondList[j] = [startj, endj] represents the start and end of the j-th interval in secondList.

Each list of intervals is pairwise disjoint and sorted in ascending order.

The task is to return the intersection of these two interval lists. The intersection of two closed intervals [a, b] and [c, d] is a new closed interval [max(a, c), min(b, d)] if they overlap, or it is empty if they do not overlap.

Return the list of intersections in sorted order.

Constraints:

• 0 <= firstList.length, secondList.length <= 1000
• firstList[i].length == 2
• secondList[j].length == 2
• 0 <= starti <= endi <= 10^9
• 0 <= startj <= endj <= 10^9
• The intervals in firstList and secondList are disjoint and sorted in ascending order.

Examples

Example 1:

Input:
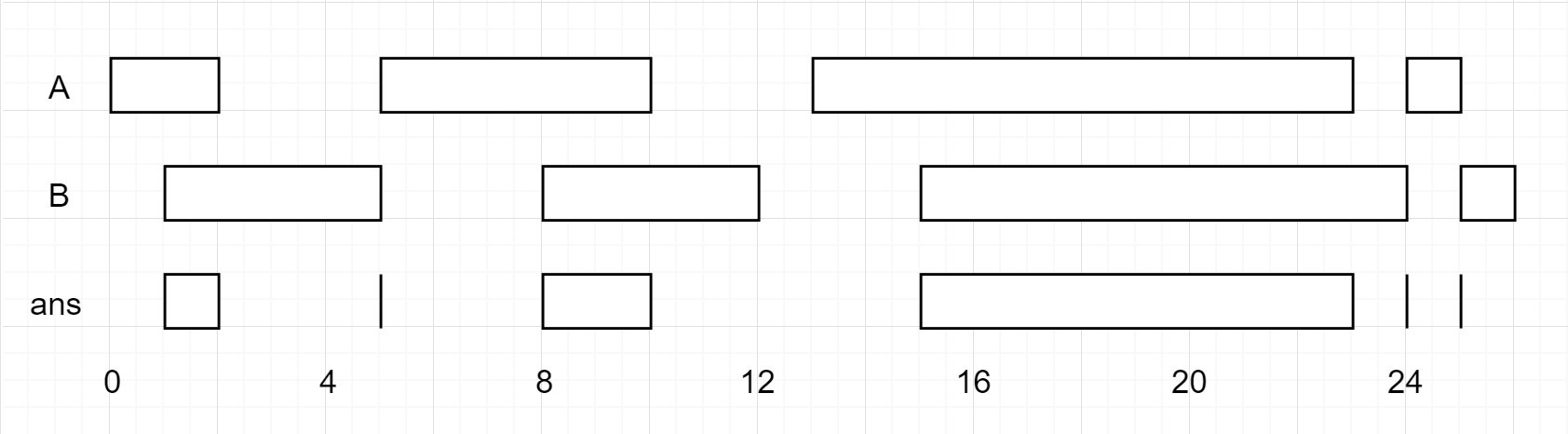
firstList = [[0, 2], [5, 10], [13, 23], [24, 25]]
secondList = [[1, 5], [8, 12], [15, 24], [25, 26]]

Output:
[[1, 2], [5, 5], [8, 10], [15, 23], [24, 24], [25, 25]]

Explanation:
- The first interval from `firstList` and `secondList` is `[0, 2]` and `[1, 5]`. The intersection is `[1, 2]`.
- The second intersection is `[5, 5]`.
- The third intersection is `[8, 10]`.
- The fourth intersection is `[15, 23]`.
- The fifth intersection is `[24, 24]`.
- The sixth intersection is `[25, 25]`.

Example 2:

Input:
firstList = [[1, 3], [5, 9]]
secondList = []

Output:
[]

Explanation:
There are no intervals in the second list, so the output is empty.

Example 3:

Input:
firstList = []
secondList = [[4, 8], [10, 12]]

Output:
[]

Explanation:
There are no intervals in the first list, so the output is empty.

Example 4:

Input:
firstList = [[1, 7]]
secondList = [[3, 10]]

Output:
[[3, 7]]

Explanation:
The only intersection is `[3, 7]` between the two intervals.

Different Approaches

1️⃣ Two-pointer Approach (Optimal)

Intuition:

Since both firstList and secondList are already sorted, we can use two pointers to traverse both lists simultaneously. At each step, we compare the current intervals from both lists and check if they overlap:

• Overlapping condition: Two intervals [start1, end1] and [start2, end2] overlap if the start of one interval is less than or equal to the end of the other. More specifically, they overlap if start1 <= end2 and start2 <= end1.
• If they overlap, the intersection is given by the maximum of the start values and the minimum of the end values.
• After processing the current intervals, we increment the pointer corresponding to the interval that ends first (since it cannot intersect with any subsequent interval).

This ensures that we process each interval once, leading to an efficient solution.

Approach:

1. Initialize two pointers, i and j, for firstList and secondList, respectively.
2. While both pointers are within the bounds of their respective lists, do the following:
   • Check if the intervals firstList[i] and secondList[j] overlap:
     • The intersection starts at max(firstList[i][0], secondList[j][0]) and ends at min(firstList[i][1], secondList[j][1]).
   • If the intervals overlap (valid intersection), add the intersection to the result list.
   • Move the pointer that points to the interval with the earlier end time (i.e., increment i if firstList[i] ends first, otherwise increment j).
3. Return the list of intersections.

Code:

#include <vector>
#include <algorithm>

using namespace std;

vector<vector<int>> intervalIntersection(vector<vector<int>>& firstList, vector<vector<int>>& secondList) {
    vector<vector<int>> result;
    int i = 0, j = 0;
    
    // Use two pointers to traverse both lists
    while (i < firstList.size() && j < secondList.size()) {
        // Find the start and end of the intersection, if any
        int start = max(firstList[i][0], secondList[j][0]);
        int end = min(firstList[i][1], secondList[j][1]);
        
        // If there is an intersection (valid intersection), add it to the result
        if (start <= end) {
            result.push_back({start, end});
        }
        
        // Move the pointer of the interval that ends first
        if (firstList[i][1] < secondList[j][1]) {
            i++;
        } else {
            j++;
        }
    }
    
    return result;
}

Complexity Analysis:

• Time Complexity:
  • O(n + m): Where n is the size of firstList and m is the size of secondList. We process each interval once with two pointers, so the total number of operations is linear with respect to the input size.
• Space Complexity:
  • O(n + m): In the worst case, the result can contain an intersection for every pair of intervals, so we need space to store the output. The extra space for the result is proportional to the number of intersections.