Problem Statement

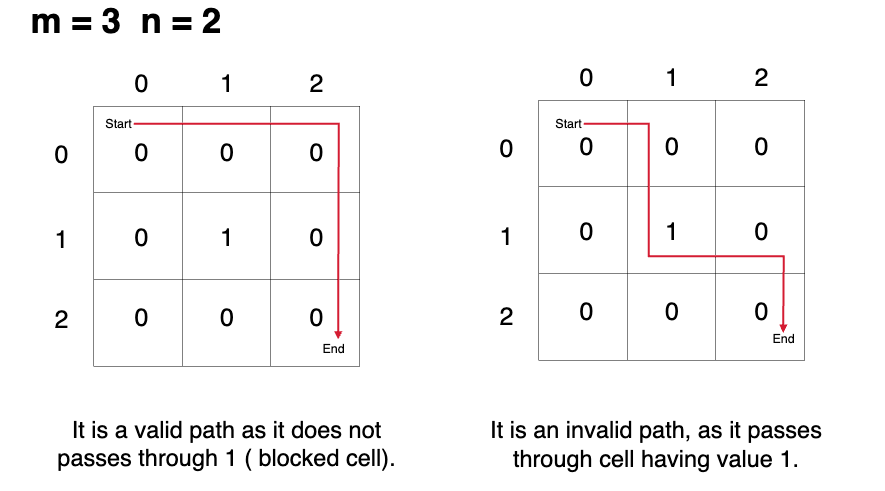
Given an m x n 2d array named matrix, where each cell is either 0 or 1. Return the number of unique ways to go from the top-left cell (matrix[0][0]) to the bottom-right cell (matrix[m-1][n-1]). A cell is blocked if its value is 1, and no path is possible through that cell.

Movement is allowed in only two directions from a cell - right and bottom.

Examples

Example 1:

Input: matrix = [[0, 0, 0], [0, 1, 0], [0, 0, 0]]
Output: 2

Explanation: The two possible paths are:
1) down -> down-> right -> right
2) right -> right -> down -> down

Example 2:

Input: matrix = [[0, 0, 0], [0, 0, 1], [0, 1, 0]]
Output: 0

Explanation: There is no way to reach the bottom-right cell.

Different Approaches

1️⃣ Recursive Approach

As we have to count all the unique ways possible to go from matrix[0,0] (top-left)to matrix[m-1,n-1](bottom-right) by only moving through the cells which have value as '0', we can try recursion to generate all possible paths and return the count of them.

Steps to form the recursive solution:

• Express the problem in terms of indexes: We are given two variables M and N, representing the dimensions of a 2D matrix. We can define the function with two parameters i and j, where i and j represent the row and column of the matrix.

We will be solving the problem in top-down manner, so f(i,j) will return total unique paths from (i,j) to (0,0) by only moving through cells having value '0', therefore at every index, we will try to move up and towards the left. Here f(i,j) represents a subproblem.

• Try out all possible choices at a given index: As we are writing a top-down recursion, at every index we have two choices, one to go up(↑) and the other to go left(←). To go upwards, we will reduce i (row)by 1, and move towards left we will reduce j (column) by 1.

/*It is pseudocode  and it is not tied to 
any specific programming  language*/

f(i,j){
    // Base case here
    
    up = f(i-1, j)
    left = f(i, j-1)
}

• Take the total of all choices: As we have to count all the possible unique paths, return the sum of the choices(up and left)

/*It is pseudocode  and it is not tied to 
any specific programming  language*/

f(i,j){
    // Base case here
    
    up = f(i-1, j)
    left = f(i, j-1)
    return up+left
}

• Base cases:
  • When i>0 and j>0 and mat[i][j] = 1, it means that the current cell is an obstacle, so we can’t find a path from here. Therefore, we return 0.
  • When i=0 and j=0, that is we have reached the destination so we can count the current path that is going on, hence we return 1.
  • When i<0 and j<0, it means that we have crossed the boundary of the matrix and we couldn’t find a right path, hence we return 0.

/*It is pseudocode  and it is not tied to 
any specific programming  language*/

f(i,j){
    if(i > 0 && j> 0 && mat[i][j] == 1)   return 0
    if(i == 0 && j == 0)   return 1
    if(i < 0 || j < 0)   return 0
}

Code:

#include <bits/stdc++.h>
using namespace std;

class Solution {
private:
    //Function to solve the problem using recursion
    int func(int i, int j, vector<vector<int>>& matrix){
        // Base case
        if (i == 0 && j == 0)  return 1;
        if(i > 0 && j > 0 && matrix[i][j] == 1)   return 0;
        if(i < 0 || j < 0)   return 0;

        /* Calculate the number of ways by
        moving up and left recursively.*/
        int up = func(i - 1, j, matrix);
        int left = func(i, j - 1, matrix);

        // Return the total ways
        return up + left;
    }
public:
    /*Function to find all unique paths to reach
    matrix[m-1][n-1] form matrix[0][0] with obstacles*/
    int uniquePathsWithObstacles(vector<vector<int>>& matrix) {
        int m = matrix.size();
        int n = matrix[0].size();
        
        //Return the total number of paths
        return func(m-1, n-1, matrix);
    }
};
int main() {
    vector<vector<int>> maze{
        {0, 0, 0},
        {0, 1, 0},
        {0, 0, 0}
    };
    
    //Create an instance of Solution class
    Solution sol;

    cout << "Number of paths with obstacles: " << sol.uniquePathsWithObstacles(maze) << endl;
    return 0;
}

Complexity Analysis:

• Time Complexity: O(2^(M+N)*(M+N)), where M is the number of row and N is the number of column in 2D array. As, each cell has 2 choices and path length is near about (M+N) and each path would take (M+N) to travel as well.
• Space Complexity: O((M-1)+(N-1)), In the worst case, the depth of the recursion can reach (M-1)+(N-1), corresponding to the maximum number of steps required to reduce both i and j to 0.

2️⃣ Memoization

If we draw the recursion tree, we will see that there are overlapping subproblems. Hence the DP approaches can be applied to the recursive solution.

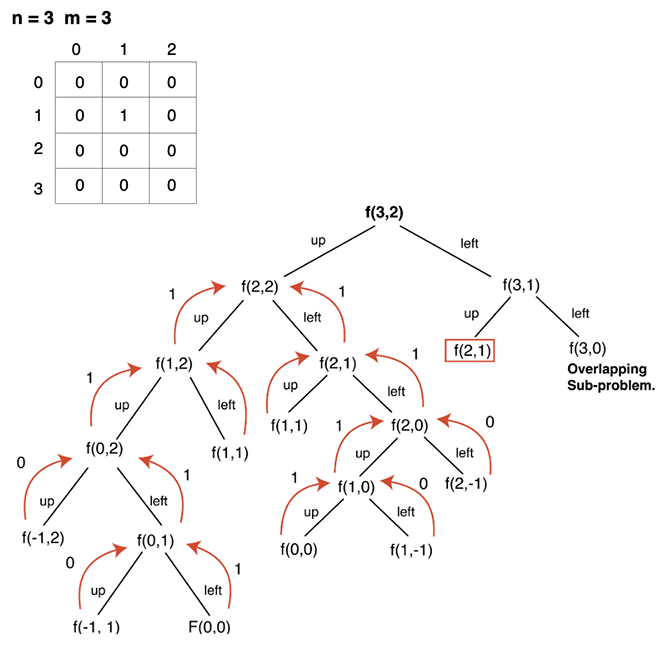
In order to convert a recursive solution to memoization the following steps will be taken:

• Declare a dp[] array of size [m][n]: As there are two changing parameters(i and j) in the recursive solution, and the maximum value they can attain is (m-1) and (n-1) respectively. So we will require a dp matrix of m*n.

The dp array stores the calculations of subproblems, dp[i][j] represents the total ways to reach (0,0) from (i,j)Initially, fill the array with -1, to indicate that no subproblem has been solved yet.

• While encountering an overlapping subproblem: When we come across a subproblem, for which the dp array has value other than -1, it means we have found a subproblem which has been solved before hence it is an overlapping subproblem. No need to calculate it's value again just retrieve the value from dp array and return it.
• Store the value of subproblem: Whenever, a subproblem is enocountered and it is not solved yet(the value at this index will be -1 in the dp array), store the calculated value of subproblem in the array.

Code:

#include <bits/stdc++.h>
using namespace std;

class Solution {
private:
    //Function to solve the problem using memoization
    int func(int i, int j, vector<vector<int>>& matrix, vector<vector<int>> &dp){
        // Base cases
        if (i == 0 && j == 0)  return 1;
        if(i > 0 && j > 0 && matrix[i][j] == 1)  return 0;
        if(i < 0 || j < 0)  return 0;
        
        // If the result is already computed, return it
        if(dp[i][j] != -1)  return dp[i][j];

        /* Calculate the number of ways by
        moving up and left recursively.*/
        int up = func(i - 1, j, matrix, dp);
        int left = func(i, j - 1, matrix, dp);

        // Return the total ways
        return dp[i][j] = up + left;
    }
public:
    /*Function to find all unique paths to reach
    matrix[m-1][n-1] form matrix[0][0] with obstacles*/
    int uniquePathsWithObstacles(vector<vector<int>>& matrix) {
        int m = matrix.size();
        int n = matrix[0].size();
        
        // Initialize DP table to memoize results
        vector<vector<int>> dp(n, vector<int>(m, -1)); 
        
        //Return the total number of paths
        return func(m-1, n-1, matrix, dp);
    }
};
int main() {
    vector<vector<int>> maze{
        {0, 0, 0},
        {0, 1, 0},
        {0, 0, 0}
    };
    
    //Create an instance of Solution class
    Solution sol;

    cout << "Number of paths with obstacles: " << sol.uniquePathsWithObstacles(maze) << endl;
    return 0;
}

Complexity Analysis:

• Time Complexity: O(M*N), where M is the number of row and N is the number of column in 2D array. At max, there will be M*N calls of recursion as the subproblems can go upto M*N.
• Space Complexity: O((N-1)+(M-1)) + O(M*N), We are using a recursion stack space: O((N-1)+(M-1)), here (N-1)+(M-1) is the path length and an external DP Array of size ‘M*N’.

3️⃣ Tabulation

Tabulation is the bottom-up approach, which means we will go from the base case to the main problem. In order to convert a recursive code to tabulation code, we try to convert the recursive code to tabulation and here are the steps:

• Declare a dp[] array of size [m][n]: As there are two changing parameters(i and j) in the recursive solution, and the maximum value they can attain is (m-1) and (n-1) respectively. So we will require a dp matrix of m*n. The dp array stores the calculations of subproblems, dp[i][j] represents the total ways to reach (0,0) from (i,j).
• Setting Base Cases in the Array: In the recursive code, we had three base cases, when i = 0 and j = 0 is 1, it means we have reached the destination and there is only one way to reach there. So put dp[0][0] = 1.
• Iterative Computation Using Loops: We can use two nested loops to have this traversal. At every cell we calculate up and left as we had done in the recursive solution. If we see the memoized code, the values required for dp[i][j] are dp[i-1][j] and dp[i][j-1]. So we only use the previous row and column value.
  • Whenever i>0 , j>0 and mat[i][j]==1, we will simply mark dp[i][j] = 0, it means that this cell is a blocked one and no path is possible through it.
• Choosing the maximum: As the question asks for total ways so update dp[i][j] as the sum of (up+left).
• Returning the last element: The last element dp[m-1][n-1] of the dp array is returned because it holds the optimal solution to the entire problem after the bottom-up computation has been completed.

Code:

#include <bits/stdc++.h>
using namespace std;

class Solution {
private:
    // Function to solve the problem using tabulation
    int func(int m, int n, vector<vector<int>>& matrix, vector<vector<int>>& dp) {
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                
                // Base conditions
                if (matrix[i][j] == 1) {
                    /* If there's an obstacle at the 
                    cell, no paths can pass through it*/
                    dp[i][j] = 0;
                    continue;
                }
                if (i == 0 && j == 0) {
                    /* If we are at the starting 
                    point, there is one path to it*/
                    dp[i][j] = 1;
                    continue;
                }

                int up = 0;
                int left = 0;

                /* Check if we can move up and left 
                (if not at the edge of the maze)*/
                if (i > 0)
                    up = dp[i - 1][j];
                if (j > 0)
                    left = dp[i][j - 1];

                /* Total number of paths to reach (i, j)
                is the sum of paths from above and left*/
                dp[i][j] = up + left;
            }
        }

        /* The final result is stored in dp[m-1][n-1],
        which represents the destination*/
        return dp[m - 1][n - 1];
    }

public:
    /* Function to find all unique paths to reach 
    matrix[m-1][n-1] from matrix[0][0] with obstacles*/
    int uniquePathsWithObstacles(vector<vector<int>>& matrix) {
        int m = matrix.size();   
        int n = matrix[0].size(); 

        // Initialize DP table to memoize results
        vector<vector<int>> dp(m, vector<int>(n, 0));

        // Return the total number of paths
        return func(m, n, matrix, dp);
    }
};

int main() {
    vector<vector<int>> maze{
        {0, 0, 0},
        {0, 1, 0},
        {0, 0, 0}
    };

    // Create an instance of Solution class
    Solution sol;

    cout << "Number of paths with obstacles: " << sol.uniquePathsWithObstacles(maze) << endl;
    return 0;
}

Complexity Analysis:

• Time Complexity: O(M*N), where M is the number of row and N is the number of column in 2D array. As the whole matrix is traversed once using two nested loops.
• Space Complexity: O(M*N), As an external DP Array of size ‘M*N’ is used to store the intermediate calculations.

4️⃣ Space Optimization

If we closely look at the relationship obltained in the tabulation approach, dp[i][j] = dp[i-1][j] + dp[i][j-1]), we see that we only need the previous row and column, in order to calculate dp[i][j]. Therefore we can space optimize it.

• Initially, we can take a dummy row ( say prev) and initialize it as 0.
• Now the current row(say temp) only needs the previous row value and the current row’s value in order to calculate dp[i][j].

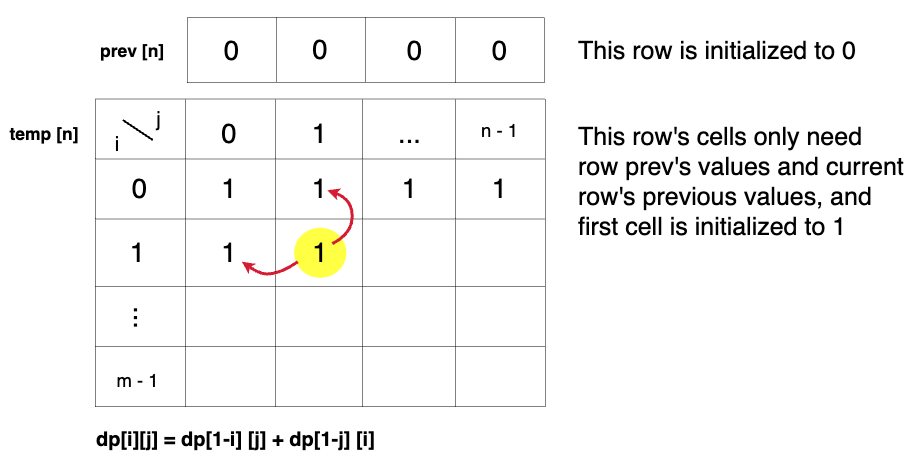
• At the next step, the 'temp' array becomes the 'prev' of the next step and using its values we can still calculate the next row’s values.

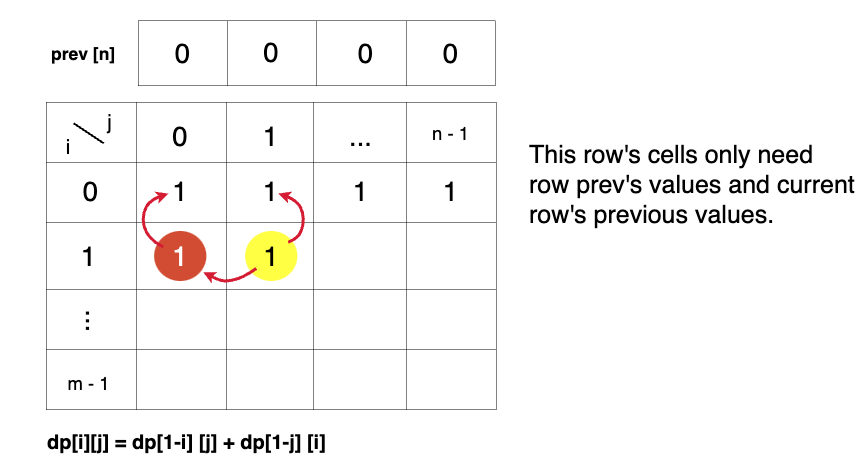
• At last prev[n-1] will give us the required answer, as it will store the total answer in top-down approach.

Code:

#include <bits/stdc++.h>
using namespace std;

class Solution {
private:
    // Function to solve the problem using space optimization
    int func(int m, int n, vector<vector<int>>& matrix) {
        /* Initialize a vector to store
        the previous row's path counts*/
        vector<int> prev(n, 0); 

        for (int i = 0; i < m; i++) {
            /* Initialize a temporary 
            vector for the current row*/
            vector<int> temp(n, 0); 
        
            for (int j = 0; j < n; j++) {
                // Base conditions
                if (i > 0 && j > 0 && matrix[i][j] == 1) {
                    /* If there's an obstacle at (i, j),
                    no paths can pass through it*/
                    temp[j] = 0; 
                    continue;
                }
                if (i == 0 && j == 0) {
                    /* If we are at the starting 
                    point, there is one path to it*/
                    temp[j] = 1; 
                    continue;
                }

                int up = 0;
                int left = 0;

                /* Check if we can move up and left
                (if not at the edge of the maze)*/
                if (i > 0)
                    up = prev[j]; 
                if (j > 0)
                    left = temp[j - 1];

                /* Total number of paths to reach (i, j)
                is the sum of paths from above and left*/
                temp[j] = up + left;
            }
            // Update the previous row with the current row
            prev = temp; 
        }

        /* The final result is stored in prev[m-1], which
        represents the destination in the last row*/
        return prev[n - 1];
    }

public:
    /* Function to find all unique paths to reach 
    matrix[m-1][n-1] from matrix[0][0] with obstacles*/
    int uniquePathsWithObstacles(vector<vector<int>>& matrix) {
        int m = matrix.size();   
        int n = matrix[0].size();

        // Return the total number of paths
        return func(m, n, matrix);
    }
};

int main() {
    vector<vector<int>> maze{
        {0, 0, 0},
        {0, 1, 0},
        {0, 0, 0},
    };

    // Create an instance of Solution class
    Solution sol;

    cout << "Number of paths with obstacles: " << sol.uniquePathsWithObstacles(maze) << endl;
    return 0;
}

Complexity Analysis:

• Time Complexity: O(M*N), where M is the number of row and N is the number of column in 2D array. As the whole matrix is traversed once using two nested loops.
• Space Complexity: O(N), We are using an external array of size ‘N’ to store only one row.