Problem Statement

Given an array of integers nums and an integer limit as the threshold value, find the smallest positive integer divisor such that dividing all the elements of the array by their divisor, the sum of the division results is less than or equal to the threshold value.

Each result of the division is rounded up to the nearest integer greater than or equal to that element (ceil). (For example: 7/3 = 3 and 10/2 = 5).

Examples

Example 1:

Input: nums = [1, 2, 3, 4, 5], limit = 8
Output: 3

Explanation:
We can get a sum of 15 (1 + 2 + 3 + 4 + 5) if we choose 1 as a divisor.
The sum is 9 (1 + 1 + 2 + 2 + 3) if we choose 2 as a divisor.
The sum is 7 (1 + 1 + 1 + 2 + 2) if we choose 3 as a divisor, which is <= 8,
the threshold value. So 3, is the minimum possible answer.

Example 2:

Input: nums = [8, 4, 2, 3], limit = 10
Ouput: 2

Explanation: If we choose 1, we get 17 as the sum.
If we choose 2, we get  9 (4 + 2 + 1 + 2) <= 10.
So, 2 is the answer.

Example 3:

Input: nums = [8, 4, 2, 3], limit = 4
Output: 8

Explanation: sum would be 4 when divided by 8 (1 + 1 + 1 + 1) = 4

Different Approaches

1️⃣ Brute Force Approach

Intuition:

The extremely naive approach is to use linear search to check all possible divisors from 1 to maximum element of the array. The minimum number for which the result is less than or equal to threshold value (limit), will be our answer.

Code:

class Solution {
public:
    // Function to find the smallest divisor such that the sum of the division results
    // does not exceed the given limit.
    int smallestDivisor(vector<int> &nums, int limit) {
        int start = 1;    // Start of the divisor range (minimum possible divisor is 1)
        int end = 0;      // End of the divisor range, which will be set to the maximum element in nums

        // Find the maximum element in nums to set as the initial end range for the divisor
        for(int i = 0; i < nums.size(); i++) {
            if(nums[i] > end) {
                end = nums[i];
            }
        }

        // Iterate through each possible divisor starting from 1 to the maximum element in nums
        for(; start <= end; start++) {
            int sum = 0;  // Sum of division results for the current divisor

            // Calculate the division result for each element in nums with the current divisor
            for(int i = 0; i < nums.size(); i++) {
                sum += ceil((double)nums[i] / (double)start);  // Add the ceiling of the division result to sum
            }

            // Check if the sum of the division results is within the limit
            if(sum <= limit) {
                return start;  // If within the limit, return the current divisor as the answer
            }
        }

        // If no divisor meets the condition, return -1 (though this should not be reached)
        return -1;
    }
};

Complexity Analysis:

• Time Complexity: O(max*N), where max is the maximum element in the array, N is size of the array. As nested loops are being used. The outer loop runs from 1 to max and the inner loop runs for N times.
• Space Complexity: As no additional space is used, so the Space Complexity is O(1).

2️⃣ Binary Search

Intuition:

Here the idea is to use binary search to efficiently solve this problem by dividing the search space into halves. As, the search space of this problem is in the range [1, max], where max is the maximum element of the array. It can be considered as a sorted space, hence binary search can be applied.

Here low = 1, because dividing by 1 gives the maximum sum. While high = max(array), because dividing by the maximum of the array element gives the minimum possible sum.

For the array [1, 2, 5, 9]

low = 1
1/1 + 2/1 + 5/1 + 9/1 = 1 + 2 + 5 + 9 = 17

high = max(array) = 9
1/9 + 2/9 + 5/9 + 9/9 = 1 + 1 + 1 + 1 = 4

Even if try to take the divisor beyound max, it remains constant.
Like we take 10 as the divisor:
1/10 + 2/10 + 5/10 + 9/10 = 1 + 1 + 1 + 1 = 4
So the possible minimum and maximum value for it is 1 and 9(the maximum element).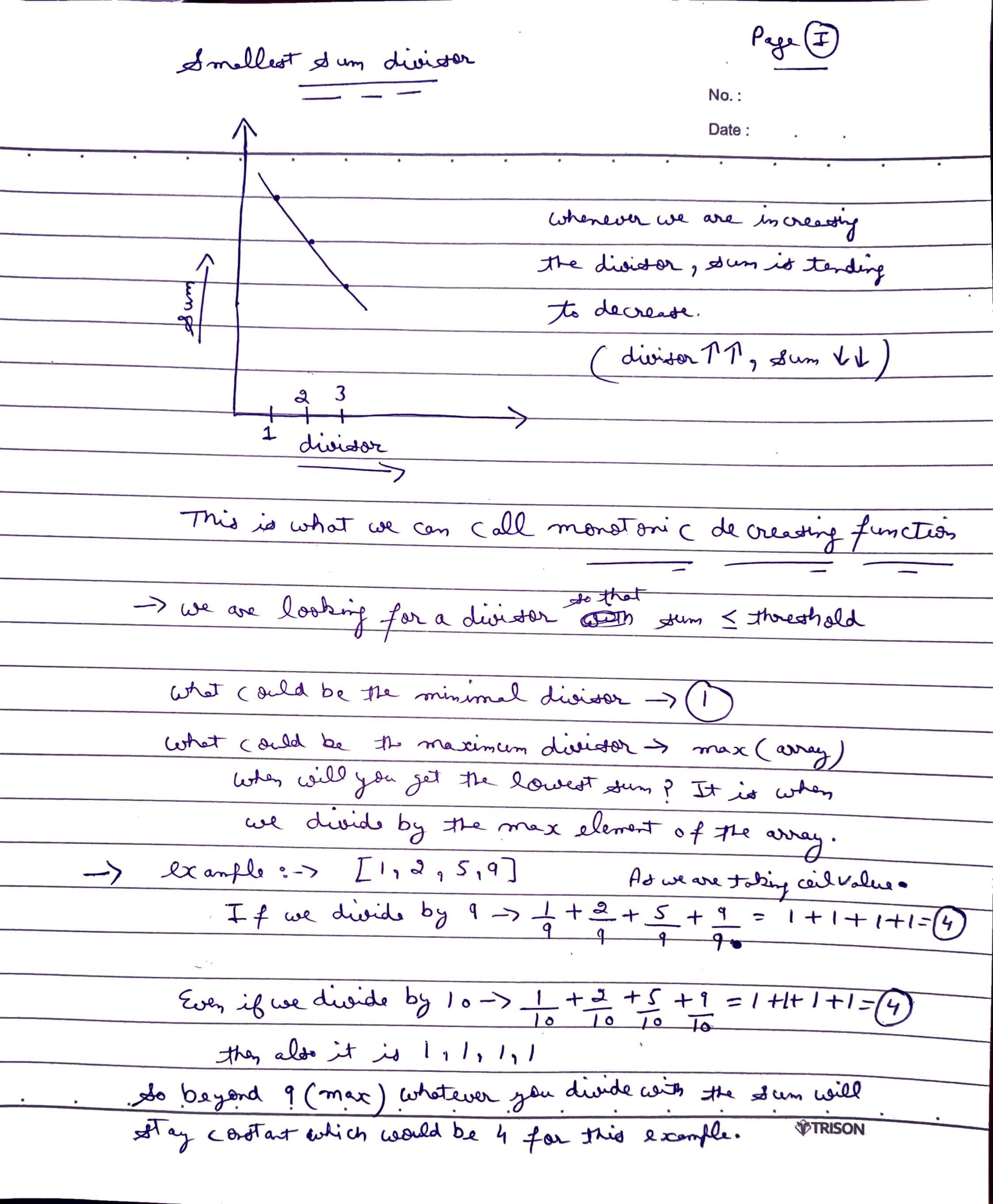

Dry Run:

Code:

class Solution {
public:
    // Function to find the smallest divisor such that the sum of the division results
    // does not exceed the given limit.
    int smallestDivisor(vector<int> &nums, int limit) {
        int start = 1;    // Start of the divisor range (minimum possible divisor is 1)
        int end = 0;      // End of the divisor range, which will be set to the maximum element in nums

        // Find the maximum element in nums to set as the initial end range for the divisor
        for(int i = 0; i < nums.size(); i++) {
            if(nums[i] > end) {
                end = nums[i];
            }
        }

        // Binary search to find the smallest divisor within the range [start, end]
        while(start <= end) {
            int mid = start + (end - start) / 2;  // Calculate mid-point of current range
            int sum = 0;  // Sum of division results for the current divisor (mid)

            // Calculate the sum of the ceiling values of each element divided by `mid`
            for(int i = 0; i < nums.size(); i++) {
                sum += ceil((double)nums[i] / mid);
            }

            // If the sum exceeds the limit, we need a larger divisor to reduce the sum
            if(sum > limit) {
                start = mid + 1;  // Move to the right half (increase `start`)
            } else {
                // If the sum is within the limit, try to find a smaller divisor
                end = mid - 1;  // Move to the left half (decrease `end`)
            }
        }

        // When the loop exits, `start` holds the smallest divisor that meets the condition
        return start;
    }
};

Complexity Analysis:

• Time Complexity: O(log(max)*N), where max is the maximum element in the array, N is size of the array.
• Space Complexity: O(1).