Problem Statement

Given two singly linked lists, find and return the node where the lists intersect. If the lists do not intersect, return null.

Examples

Example 1:

Input: List1 = {1, 3, 1, 1, 2, 4}, List2 = {3, 2, 4}

Output: 2

Explanation: Here, both lists intersection nodes start from node 2.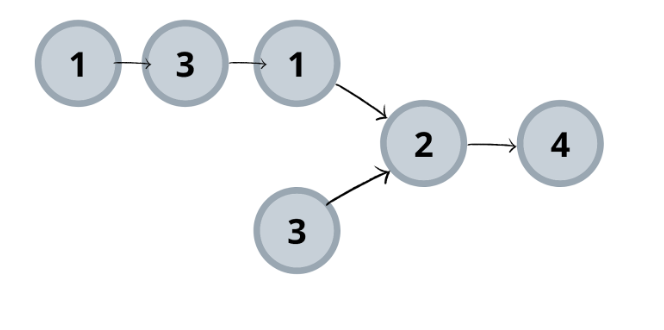

Example 2:

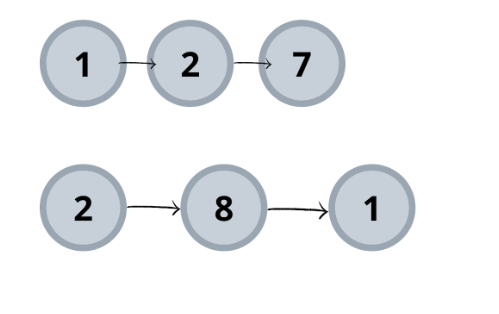
Input: List1 = {1, 2, 7}, List2 = {2, 8, 9}

Output: Null

Explanation: Here, both lists do not intersect and thus no intersection node is present.

Different Approaches

1️⃣ Brute Force Approach

Intuition:

For each node in the first list, traverse the second list and check if there is any node that matches.

Code:

#include<iostream>
using namespace std;

class node {
    public:
        int num;
        node* next;
        node(int val) {
            num = val;
            next = NULL;
        }
};
//utility function to insert node at the end of the linked list
void insertNode(node* &head,int val) {
    node* newNode = new node(val);
    
    if(head == NULL) {
        head = newNode;
        return;
    }
    
    node* temp = head;
    while(temp->next != NULL) temp = temp->next;
    
    temp->next = newNode;
    return;
}

//utility function to check presence of intersection
node* intersectionPresent(node* head1, node* head2) {
    while(head2 != NULL) {
        node* temp = head1;
        while(temp != NULL) {
            //if both nodes are same
            if(temp == head2) return head2;
            temp = temp->next;
        }
        head2 = head2->next;
    }
    //intersection is not present between the lists return null
    return NULL;
}

//utility function to print linked list created
void printList(node* head) {
    while(head->next != NULL) {
        cout<<head->num<<"->";
        head = head->next;
    }
    cout<<head->num<<endl;
}

int main() {
    // creation of both lists 
    node* head = NULL;
    insertNode(head,1);
    insertNode(head,3);
    insertNode(head,1);
    insertNode(head,2);
    insertNode(head,4);
    node* head1 = head;
    head = head->next->next->next;
    node* headSec = NULL;
    insertNode(headSec,3);
    node* head2 = headSec;
    headSec->next = head;
    //printing of the lists
    cout<<"List1: "; printList(head1);
    cout<<"List2: "; printList(head2);
    //checking if intersection is present
    node* answerNode = intersectionPresent(head1,head2);
    if(answerNode == NULL )
    cout<<"No intersection\n";
    else
    cout<<"The intersection point is "<<answerNode->num<<endl;
    return 0;
}

// Output
List1: 1->3->1->2->4
List2: 3->2->4
The intersection point is 2

Complexity Analysis:

Time Complexity: O(m*n)

• For each node in the list 2 entire lists 1 are iterated.

Space Complexity: O(1)

• No extra space is used.

2️⃣ Hashing

Intuition:

The brute force approach is not much efficient as time complexity attains O(m*n). In brute force, we are basically performing searching. We can also perform searches by Hashing. Taking into consideration that hashing process takes O(1) time complexity.

• Iterate through list 1 and hash its node address.
• Iterate through list 2 and search the hashed value in the hash table. If found, return node.

Code:

#include<bits/stdc++.h>
using namespace std;

class node {
    public:
        int num;
        node* next;
        node(int val) {
            num = val;
            next = NULL;
        }
};
//utility function to insert node at the end of the linked list
void insertNode(node* &head,int val) {
    node* newNode = new node(val);
    
    if(head == NULL) {
        head = newNode;
        return;
    }
    
    node* temp = head;
    while(temp->next != NULL) temp = temp->next;
    
    temp->next = newNode;
    return;
}

//utility function to check presence of intersection
node* intersectionPresent(node* head1,node* head2) {
     unordered_set<node*> st;
    while(head1 != NULL) {
       st.insert(head1);
       head1 = head1->next;
    }
    while(head2 != NULL) {
        if(st.find(head2) != st.end()) return head2;
        head2 = head2->next;
    }
    return NULL;

}

//utility function to print linked list created
void printList(node* head) {
    while(head->next != NULL) {
        cout<<head->num<<"->";
        head = head->next;
    }
    cout<<head->num<<endl;
}

int main() {
    // creation of both lists 
    node* head = NULL;
    insertNode(head,1);
    insertNode(head,3);
    insertNode(head,1);
    insertNode(head,2);
    insertNode(head,4);
    node* head1 = head;
    head = head->next->next->next;
    node* headSec = NULL;
    insertNode(headSec,3);
    node* head2 = headSec;
    headSec->next = head;
    //printing of the lists
    cout<<"List1: "; printList(head1);
    cout<<"List2: "; printList(head2);
    //checking if intersection is present
    node* answerNode = intersectionPresent(head1,head2);
    if(answerNode == NULL )
    cout<<"No intersection\n";
    else
    cout<<"The intersection point is "<<answerNode->num<<endl;
    return 0;
}

// Output
List1: 1->3->1->2->4
List2: 3->2->4
The intersection point is 2

Complexity Analysis:

Time Complexity: O(n+m)

• Iterating through list 1 first takes O(n), then iterating through list 2 takes O(m).

Space Complexity: O(n)

• Storing list 1 node addresses in unordered_set.

3️⃣ Difference in Length

Intuition:

We will reduce the search length. This can be done by searching the length of the shorted linked list.

1. Find the length of both lists.
2. Find the positive difference between these lengths.
3. Move the dummy pointer of the larger list by the difference achieved. This makes our search length reduced to a smaller list length.
4. Move both pointers, each pointing two lists, ahead simultaneously if both do not collide.

Code:

#include<bits/stdc++.h>
using namespace std;

class node {
    public:
        int num;
        node* next;
        node(int val) {
            num = val;
            next = NULL;
        }
};
//utility function to insert node at the end of the linked list
void insertNode(node* &head,int val) {
    node* newNode = new node(val);
    
    if(head == NULL) {
        head = newNode;
        return;
    }
    
    node* temp = head;
    while(temp->next != NULL) temp = temp->next;
    
    temp->next = newNode;
    return;
}
int getDifference(node* head1,node* head2) {
     int len1 = 0,len2 = 0;
        while(head1 != NULL || head2 != NULL) {
            if(head1 != NULL) {
                ++len1; head1 = head1->next;
            }
            if(head2 != NULL) {
                ++len2; head2 = head2->next;
            }
            
        }
        return len1-len2;//if difference is neg-> length of list2 > length of list1 else vice-versa
}

//utility function to check presence of intersection
node* intersectionPresent(node* head1,node* head2) {
 int diff = getDifference(head1,head2);
        if(diff < 0) 
            while(diff++ != 0) head2 = head2->next; 
        else while(diff-- != 0) head1 = head1->next;
        while(head1 != NULL) {
            if(head1 == head2) return head1;
            head2 = head2->next;
            head1 = head1->next;
        }
        return head1;


}

//utility function to print linked list created
void printList(node* head) {
    while(head->next != NULL) {
        cout<<head->num<<"->";
        head = head->next;
    }
    cout<<head->num<<endl;
}

int main() {
    // creation of both lists 
    node* head = NULL;
    insertNode(head,1);
    insertNode(head,3);
    insertNode(head,1);
    insertNode(head,2);
    insertNode(head,4);
    node* head1 = head;
    head = head->next->next->next;
    node* headSec = NULL;
    insertNode(headSec,3);
    node* head2 = headSec;
    headSec->next = head;
    //printing of the lists
    cout<<"List1: "; printList(head1);
    cout<<"List2: "; printList(head2);
    //checking if intersection is present
    node* answerNode = intersectionPresent(head1,head2);
    if(answerNode == NULL )
    cout<<"No intersection\n";
    else
    cout<<"The intersection point is "<<answerNode->num<<endl;
    return 0;
}

// Output
List1: 1->3->1->2->4
List2: 3->2->4
The intersection point is 2

Complexity Analysis:

• Time Complexity:  O(2 max(length of list1, length of ist2)) + O(abs(length of list1 - length of list2)) + O(min (length of list1, length of list2))
  • Finding the length of both lists takes max(length of list1, length of list2) because it is found simultaneously for both of them. Moving the head pointer ahead by a difference of them.
• Space Complexity: O(1)
  • No extra space is used.