Problem Statement
Given a rod of length N inches and an array price[] where price[i] denotes the value of a piece of rod of length i inches (1-based indexing). Determine the maximum value obtainable by cutting up the rod and selling the pieces. Make any number of cuts, or none at all, and sell the resulting pieces.
Examples
Example 1:
Input: price = [1, 6, 8, 9, 10, 19, 7, 20], N = 8
Output: 25
Explanation: Cut the rod into lengths of 2 and 6 for a
total price of 6 + 19 = 25Example 2:
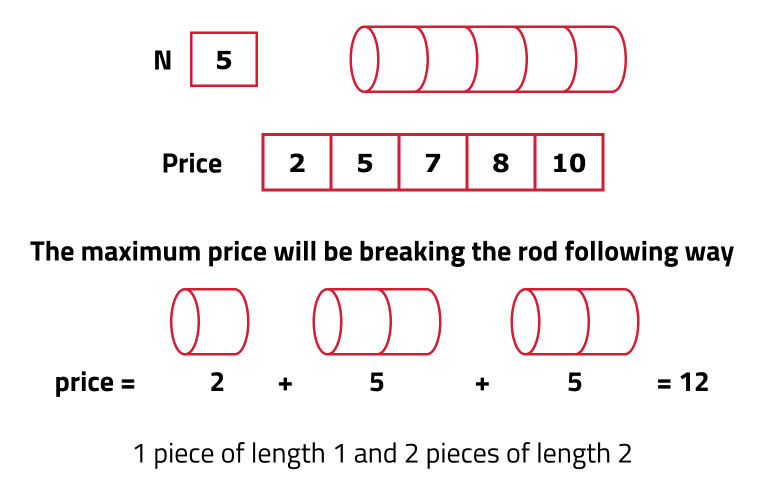
Input: price = [1, 5, 8, 9], N = 4
Output: 10
Explanation: Cut the rod lengths of 2 and 2 for a
total price of 5 + 5 = 10Different Approaches
1️⃣ Recursive Approach
Understanding:
In order to solve the problem, we can build the intuition in a bit different way. Instead of cutting the rod into pieces, try to think that we need to make a rod of length 'N'(as given in the problem). Then the question becomes quite similar to unbounded knapsack problem that we did earlier, where we were doing similar work of filling up the knapsack of certain weight 'W'.
Try to pick various length in all possible ways and sum them up to make a rod of length 'N'. As we need to think of all possible ways, recursion can be used to solve this problem.
Steps to form the recursive solution:
- Express the problem in terms of indexes: We are given ‘n’ items, where n is the size of the array. Their price is represented by the ‘price’ array. So clearly one parameter will be ‘ind’, i.e index upto which the array items are being considered. There is one more parameter 'N'. It keeps track of the total length of the rod that needs to be cut into parts.
- So initially, we need to find f(n-1, N) where N is the total length of the rod given to us. f(n-1, N) will give the maximum value that can be acquired by cutting the rod with values from index 0 to n-1 and length of the rod N.
- Try out all possible choices at a given index: As all the length needs to be explored, we will use the pick/non-pick technique. There will be two choices in each function call:
- Do not include the current element in the subset: First try to find a length without considering the current index element. For this, make a recursive call to f(ind-1,target).
- Include the current element in the subset: Now try to make the rod by considering the current index element as part of rod. As the current element(arr[ind]) is included, the remaining target length will be target - arr[ind]. Therefore, make a function call of f(ind,target-arr[ind]). As there are infinite supply of rods, we can stand at the same index after picking the element at an index.
Note: Consider the current element in the length of the rod only when the current length is less or equal to the 'N'.
/*It is pseudocode and it is not tied to
any specific programming language*/
f(ind, N){
not pick = 0+f(ind-1, N)
pick = INT_MIN
rod length = ind+1
if( rod length <= N){
pick = price[ind] + f(ind, N - rod length)
}
}- Return max(pick and not pick): As we are looking for maximum price that we can get, so take maximum of both the choices.
/*It is pseudocode and it is not tied to
any specific programming language*/
f(ind, N){
not pick = 0+f(ind-1, N)
pick = INT_MIN
rod length = ind+1
if(rod length <= N){
pick = price[ind] + f(ind, N - rod length)
}
return max(pick, not pick)
}- Base cases:
- If ind==0, it means for now the rod length will be 1(ind+1). In order to make a rod length of 'N' we can take the rod of length '1' for 'N' times. So the total price will be N*price[0] and we will return this for the base case.
Code:
class Solution {
public:
// Recursive function to find the maximum profit from rod cutting
int maximizeProfit(vector<int>& prices, int currentIndex, int remainingLength) {
// Base case: If no length is remaining or we've considered all lengths
if (currentIndex >= prices.size() || remainingLength <= 0) {
return 0;
}
// Option 1: Include the current piece if possible
int includeProfit = INT_MIN;
if (currentIndex + 1 <= remainingLength) { // Convert index to rod length (1-based)
includeProfit = prices[currentIndex] +
maximizeProfit(prices, currentIndex, remainingLength - (currentIndex + 1));
}
// Option 2: Exclude the current piece and move to the next piece
int excludeProfit = maximizeProfit(prices, currentIndex + 1, remainingLength);
// Return the maximum profit from the two options
return max(includeProfit, excludeProfit);
}
// Public function to start the recursion for rod cutting
int rodCutting(vector<int>& prices, int rodLength) {
return maximizeProfit(prices, 0, rodLength);
}
};
2️⃣ Memoization
class Solution {
public:
// Recursive function with memoization to maximize profit
int maximizeProfit(vector<int>& prices, int currentIndex, int remainingLength, vector<vector<int>>& dp) {
// Base case: If no length is remaining or we've considered all lengths
if (currentIndex >= prices.size() || remainingLength <= 0) {
return 0;
}
// If already computed, return the cached value
if (dp[currentIndex][remainingLength] != -1) {
return dp[currentIndex][remainingLength];
}
// Option 1: Include the current piece if possible
int includeProfit = INT_MIN;
if (currentIndex + 1 <= remainingLength) { // Convert index to rod length
includeProfit = prices[currentIndex] +
maximizeProfit(prices, currentIndex, remainingLength - (currentIndex + 1), dp);
}
// Option 2: Exclude the current piece and move to the next piece
int excludeProfit = maximizeProfit(prices, currentIndex + 1, remainingLength, dp);
// Store the result in the dp table
return dp[currentIndex][remainingLength] = max(includeProfit, excludeProfit);
}
// Public function to start recursion with memoization
int rodCutting(vector<int>& prices, int rodLength) {
vector<vector<int>> dp(prices.size(), vector<int>(rodLength + 1, -1));
return maximizeProfit(prices, 0, rodLength, dp);
}
};