Problem Statement

Given two integers m and n, representing the number of rows and columns of a 2d array named matrix. Return the number of unique ways to go from the top-left cell (matrix[0][0]) to the bottom-right cell (matrix[m-1][n-1]).

Movement is allowed only in two directions from a cell: right and bottom.

Examples

Example 1:

Input: m = 3, n = 2
Output: 3

Explanation: There are 3 unique ways to go from the top left to the bottom right cell.
1) right->down->down
2) down->right->down
3) down->down->right

Example 2:

Input: m = 2, n = 4
Output: 4

Explanation: There are 4 unique ways to go from the top left to the bottom right cell.
1) down -> right -> right -> right
2) right -> down -> right -> right
3) right -> right -> down -> right
4) right -> right -> right -> down

Different Approaches

1️⃣ Recursive Approach (Top Down)

As we have to count all possible ways to go from matrix[0,0] (top-left)to matrix[m-1,n-1](bottom-right), we can try recursion to generate all possible paths.

Steps to form the recursive solution:

• Express the problem in terms of indexes: We are given two variables M and N, representing the dimensions of a 2D matrix. We can define the function with two parameters i and j, where i and j represent the row and column of the matrix. f(i,j) will defines a subproblem, and it will return total unique paths from (i,j) to (0,0).

f(i,j) will give us a sub-answer for the region (marked in blue) below:

We will be doing a top-down recursion, i.e we will move from the cell[M-1][N-1] and try to find our way to the cell[0][0]. Therefore at every index, we will try to move up and towards the left.

• Try out all possible choices at a given index: As we are writing a top-down recursion, at every index we have two choices, one to go up(↑) and the other to go left(←). To go upwards, we will reduce i (row)by 1, and move towards left we will reduce j (column) by 1.

/*It is pseudocode  and it is not tied to 
any specific programming  language*/

f(i,j){
    //Base case here
    
    up = f(i-1, j)
    left = f(i, j-1)
}

• Take the total of all choices: As we have to count all the possible unique paths, return the sum of the choices(up and left).

/*It is pseudocode  and it is not tied to 
any specific programming  language*/

f(i,j){
    //Base case here
    
    up = f(i-1, j)
    left = f(i, j-1)
    return up+left
}

• Base cases: There will be two base cases, when i=0 and j=0, that is we have reached the destination so we can count the current path that is going on, hence we return 1. When i<0 and j<0, it means that we have crossed the boundary of the matrix and we couldn’t find a right path, hence we return 0.

Code:

 #include <bits/stdc++.h>
using namespace std;

class Solution {
private:
    //Function to solve the problem using recursion
    int func(int i, int j){
        // Base case
        if (i == 0 && j == 0)  return 1;

        /* If we go out of bounds or reach 
        a blocked cell, there are no ways.*/
        if (i < 0 || j < 0)  return 0;

        /* Calculate the number of ways by
        moving up and left recursively.*/
        int up = func(i - 1, j);
        int left = func(i, j - 1);

        // Return the total ways
        return up + left;
    }
public:
    /*Function to count the total ways
    to reach (0,0) from (m-1,n-1)*/
    int uniquePaths(int m, int n) {
        //Return the total count(0 based indexing)
        return func(m-1,n-1);
    }
};
int main() {
    int m = 3;
    int n = 2;
    
    //Create an instance of Solution class
    Solution sol;
    
    // Call the countWays function and print the result.
    cout << "Number of ways: " << sol.uniquePaths(m, n) << endl;

    return 0;
}

Complexity Analysis:

• Time Complexity: O(2^(M+N)*(M+N)), where M is the number of row and N is the number of column in 2D array. As, each cell has 2 choices and path length is near about (M+N) and each path would take (M+N) to travel as well.
• Space Complexity: O((M-1)+(N-1)), In the worst case, the depth of the recursion can reach (M-1)+(N-1), corresponding to the maximum number of steps required to reduce both i and j to 0.

2️⃣ Memoization

If we draw the recursion tree, we will see that there are overlapping subproblems. Hence the DP approaches can be applied to the recursive solution.

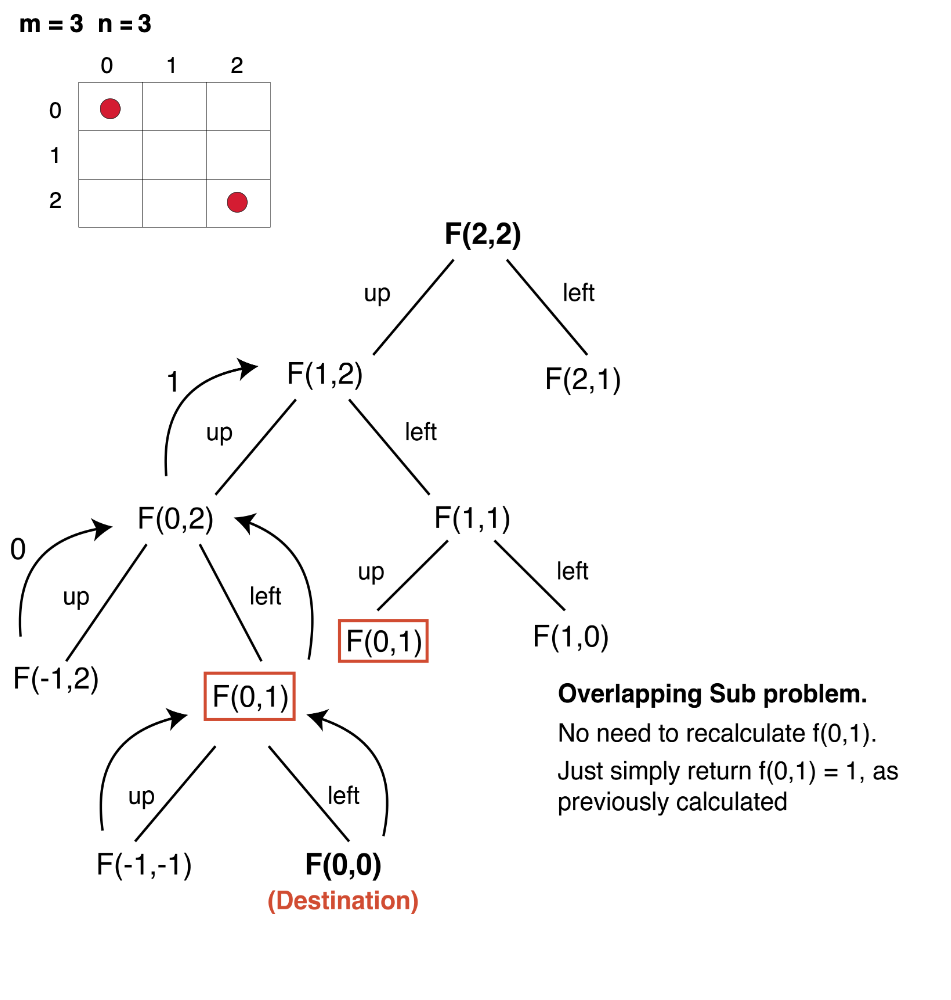
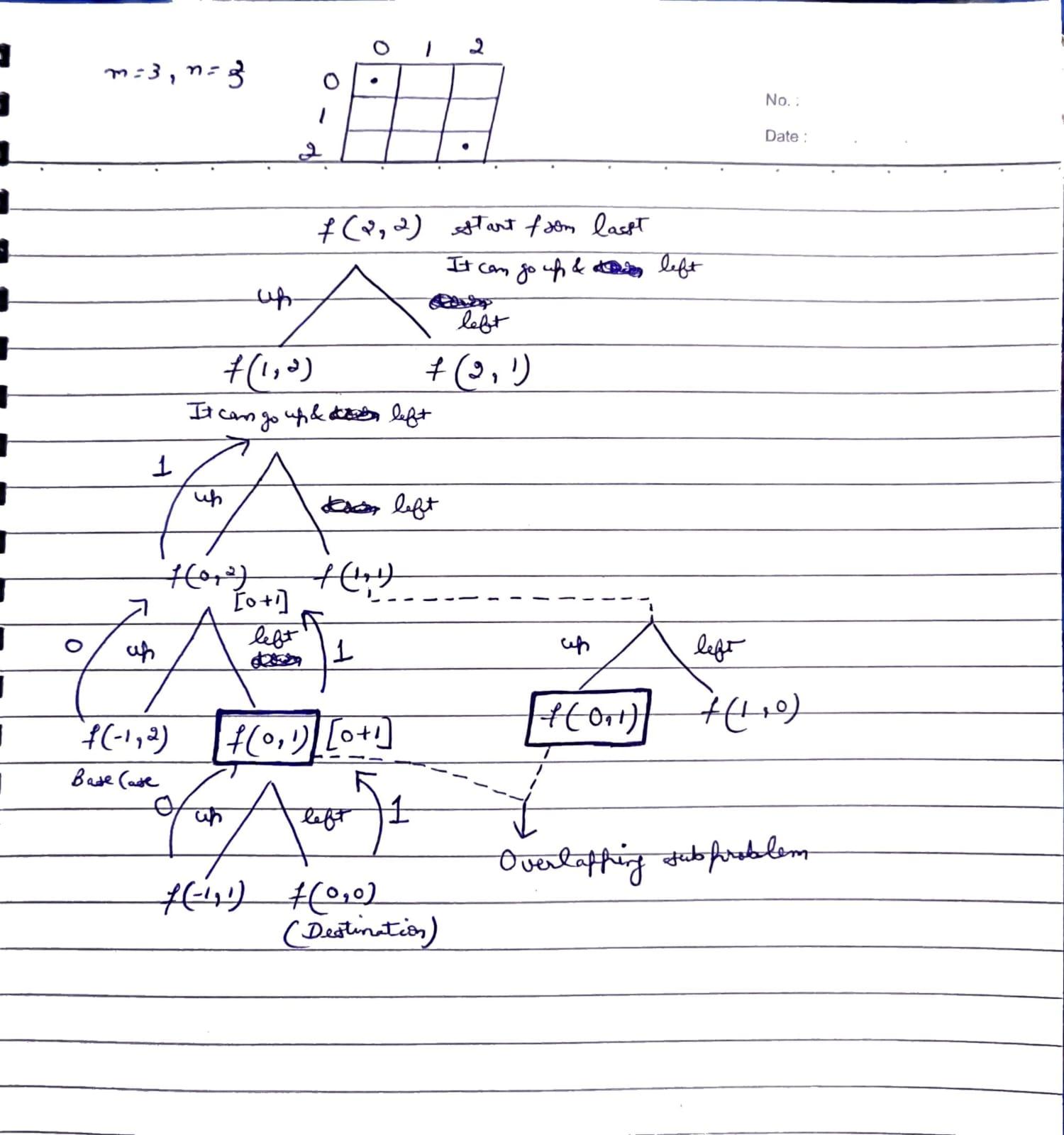
The Shortest trick to apply memoization is to check for changing parameters. In this case we have row and column.

In order to convert a recursive solution to memoization the following steps will be taken:

• Declare a dp[] array of size [m][n]: As there are two changing parameters(i and j) in the recursive solution, and the maximum value they can attain is (m-1) and (n-1) respectively. So we will require a dp matrix of m*n.

The dp array stores the calculations of subproblems, dp[i][j] represents the total ways to reach (0,0) from (i,j)Initially, fill the array with -1, to indicate that no subproblem has been solved yet.

• While encountering an overlapping subproblem: When we come across a subproblem, for which the dp array has value other than -1, it means we have found a subproblem which has been solved before hence it is an overlapping subproblem. No need to calculate it's value again just retrieve the value from dp array and return it.
• Store the value of subproblem: Whenever, a subproblem is encountered and it is not solved yet(the value at this index will be -1 in the dp array), store the calculated value of subproblem in the array.

Code:

#include <bits/stdc++.h>
using namespace std;

class Solution {
private:
    //Function to solve the problem using recursion
    int func(int i, int j, vector<vector<int>>& dp){
        // Base case
        if (i == 0 && j == 0)  return 1;

        /* If we go out of bounds or reach 
        a blocked cell, there are no ways.*/
        if (i < 0 || j < 0)  return 0;
        
        /* If we have already computed the number 
        of ways for this cell, return it.*/
        if (dp[i][j] != -1)  return dp[i][j];

        /* Calculate the number of ways by
        moving up and left recursively.*/
        int up = func(i - 1, j, dp);
        int left = func(i, j - 1, dp);

        // Store the result in dp table and return it.
        return dp[i][j] = up + left;
    }
public:
    /*Function to count the total ways
    to reach (0,0) from (m-1,n-1)*/
    int uniquePaths(int m, int n) {
        /* Initialize a memoization table (dp) to
        store the results of subproblems.*/
        vector<vector<int>> dp(m, vector<int>(n, -1));
        
        //Return the total count(0 based indexing)
        return func(m-1,n-1, dp);
    }
};
int main() {
    int m = 3;
    int n = 2;
    
    //Create an instance of Solution class
    Solution sol;
    
    // Call the countWays function and print the result.
    cout << "Number of ways: " << sol.uniquePaths(m, n) << endl;

    return 0;
}

Complexity Analysis:

• Time Complexity: O(M*N), where M is the number of row and N is the number of column in 2D array. At max, there will be M*N calls of recursion as the subproblems can go upto M*N.
• Space Complexity: O((N-1)+(M-1)) + O(M*N), We are using a recursion stack space: O((N-1)+(M-1)), here (N-1)+(M-1) is the path length and an external DP Array of size ‘M*N’.

3️⃣ Tabulation

Tabulation is the bottom-up approach, which means we will go from the base case to the main problem. In order to convert a recursive code to tabulation code, we try to convert the recursive code to tabulation and here are the steps:

• Declare a dp[] array of size [m][n]: As there are two changing parameters(i and j) in the recursive solution, and the maximum value they can attain is (m-1) and (n-1) respectively. So we will require a dp matrix of m*n. The dp array stores the calculations of subproblems, dp[i][j] represents the total ways to reach (0,0) from (i,j).
• Setting Base Cases in the Array: In the recursive code, we knew the answer for base case, when i = 0 and j = 0 is 1, it means we have reached the destination and there is only one way to reach there. So put dp[0][0] = 1.
• Iterative Computation Using Loops: We can use two nested loops to have this traversal. At every cell we calculate up and left as we had done in the recursive solution. If we see the memoized code, the values required for dp[i][j] are dp[i-1][j] and dp[i][j-1]. So we only use the previous row and column value.
• Choosing the maximum: As the question asks for total ways so update dp[i][j] as the sum of (up+left).
• Returning the last element: The last element dp[m-1][n-1] of the dp array is returned because it holds the optimal solution to the entire problem after the bottom-up computation has been completed.

Code:

#include <bits/stdc++.h>
using namespace std;

class Solution {
private:
    //Function to solve the problem using tabulation
    int func(int m, int n, vector<vector<int>>& dp){
        // Loop through the grid using two nested loops
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                
            // Base condition
            if (i == 0 && j == 0) {
                dp[i][j] = 1;
                /* Skip the rest of the loop and 
                continue with the next iteration.*/
                continue; 
            }

            /* Initialize variables to store the number 
            of ways from cell above (up) and left (left)*/
            int up = 0;
            int left = 0;

            /* If we are not at first row (i > 0), update 
            'up' with the value from the cell above.*/
            if (i > 0)
                up = dp[i - 1][j];

            /* If we are not at the first column (j > 0),
            update 'left' with value from the cell to left.*/
            if (j > 0)
                left = dp[i][j - 1];

            /* Calculate the number of ways to reach the 
            current cell by adding 'up' and 'left'.*/
            dp[i][j] = up + left;
        }
    }

    // The result is stored in bottom-right cell (m-1, n-1).
    return dp[m - 1][n - 1];
}
public:
    /*Function to count the total ways
    to reach (0,0) from (m-1,n-1)*/
    int uniquePaths(int m, int n) {
        /* Initialize a memoization table (dp) to
        store the results of subproblems.*/
        vector<vector<int>> dp(m, vector<int>(n, -1));
        
        //Return the total count(0 based indexing)
        return func(m, n, dp);
    }
};
int main() {
    int m = 3;
    int n = 2;
    
    //Create an instance of Solution class
    Solution sol;
    
    // Call the countWays function and print the result.
    cout << "Number of ways: " << sol.uniquePaths(m, n) << endl;

    return 0;
}

Complexity Analysis:

• Time Complexity: O(M*N), where M is the number of row and N is the number of column in 2D array. As the whole matrix is traversed once using two nested loops.
• Space Complexity: O(M*N), As an external DP Array of size ‘M*N’ is used to store the intermediate calculations.

4️⃣ Space Optimized Approach

If we closely look at the relationship obtained in the tabulation approach, dp[i][j] = dp[i-1][j] + dp[i][j-1]), we see that we only need the previous row and column, in order to calculate dp[i][j]. Therefore we can space optimize it.

• Initially, we can take a dummy row ( say prev) and initialize it as 0.
• Now the current row(say temp) only needs the previous row value and the current row’s value in order to calculate dp[i][j].

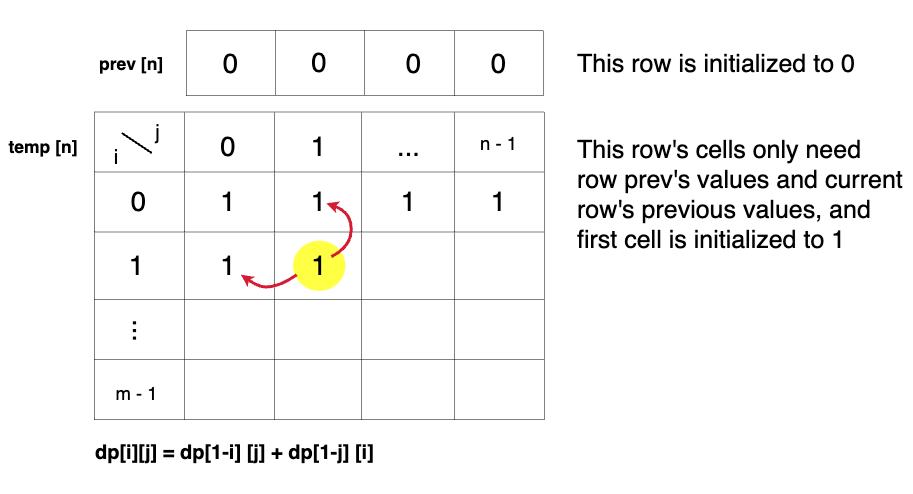
• At the next step, the 'temp' array becomes the 'prev' of the next step and using its values we can still calculate the next row’s values.

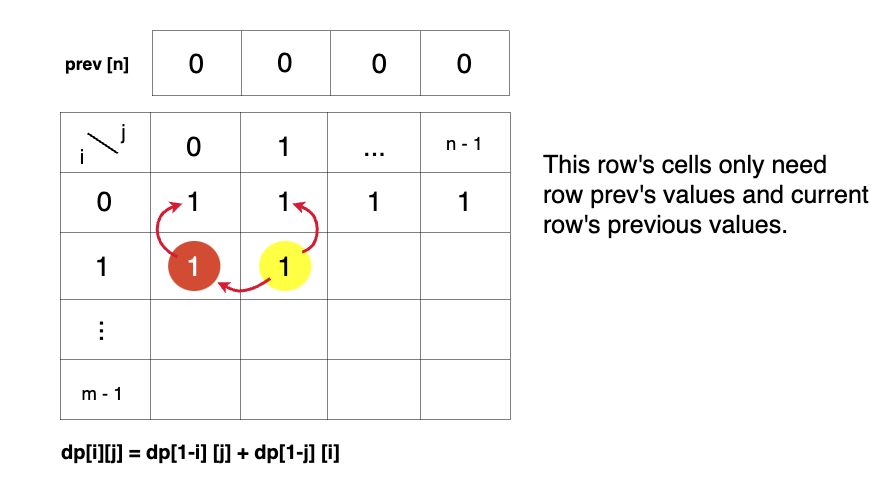
• At last prev[n-1] will give us the required answer, as it will store the total answer in top-down approach.

Code:

#include <bits/stdc++.h>
using namespace std;

class Solution {
private:
    //Function to solve the problem using space optimization.
    int func(int m, int n){
        /* Initialize a vector to represent 
        the previous row of the grid.*/
        vector<int> prev(n, 0);

        // Iterate through the rows of the grid.
        for (int i = 0; i < m; i++) {
            /* Create a temporary vector to
            represent the current row.*/
            vector<int> temp(n, 0);

            for (int j = 0; j < n; j++) {
                // Base case
                if (i == 0 && j == 0) {
                    temp[j] = 1;
                    continue;
                }

            /* Initialize variables to store the number
            of ways from the cell above (up) and left (left).*/
            int up = 0;
            int left = 0;

            /* If we are not at the first row (i > 0), update
            'up' with the value from the previous row.*/
            if (i > 0)
                up = prev[j];

            /* If we are not at the first column (j > 0),
            update 'left' with the value from current row.*/
            if (j > 0)
                left = temp[j - 1];

            /* Calculate the number of ways to reach the
            current cell by adding 'up' and 'left'.*/
            temp[j] = up + left;
        }

        /* Update the previous row with values 
        calculated for the current row.*/
        prev = temp;
    }

    /* The result is stored in the last
    cell of the previous row (n-1).*/
    return prev[n - 1];
}
public:
    /*Function to count the total ways
    to reach (0,0) from (m-1,n-1)*/
    int uniquePaths(int m, int n) {
        
        //Return the total count(0 based indexing)
        return func(m, n);
    }
};
int main() {
    int m = 3;
    int n = 2;
    
    //Create an instance of Solution class
    Solution sol;
    
    // Call the countWays function and print the result.
    cout << "Number of ways: " << sol.uniquePaths(m, n) << endl;

    return 0;
}

Complexity Analysis:

• Time Complexity: O(M*N), where M is the number of row and N is the number of column in 2D array. As the whole matrix is traversed once using two nested loops.
• Space Complexity: O(N), We are using an external array of size ‘N’ to store only one row.