What is Recursion?

Recursion occurs when a function calls itself either directly or indirectly as part of its execution. The main idea behind recursion is that a larger problem can often be solved by solving smaller instances of the same problem and combining the results.

When a function calls itself until a specified condition is met.

Recursion is the process of defining a problem (or the solution to a problem) in terms of (a simpler version of) itself.

For example, we can define the operation "find your way home" as:

If you are at home, stop moving.
Take one step toward home.
"find your way home".

Here the solution to finding your way home is two steps (three steps).

• First, we don't go home if we are already home.
• Secondly, we do a very simple action that makes our situation simpler to solve.
• Finally, we redo the entire algorithm.

The above example is called tail recursion. This is where the very last statement is calling the recursive algorithm. Tail recursion can directly be translated into loops.

Every recursive function has three main parts:

1. Base Case: The condition under which the function stops calling itself. It prevents the recursion from continuing indefinitely. (i.e., when to stop)
2. Word toward Base Case: Where we make the problem simpler, like dividing the list into two parts, each smaller than the original
3. Recursive Case: The part of the function where it calls itself to solve a smaller subproblem. (i.e., call ourselves)

Key Characteristics of Recursion

• Base Case: Every recursion must have a base case, which acts as a stopping condition. Without a base case, the recursion would continue infinitely, leading to a stack overflow.
• Recursive Call: In each recursive call, the problem size is reduced, moving closer to the base case.

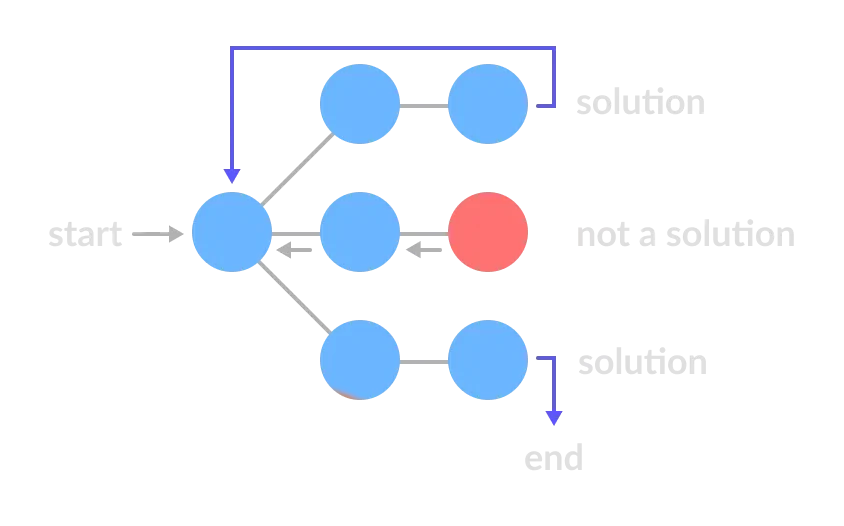
• Backtracking: It is a general algorithmic technique (approach) for solving problems incrementally by building solutions piece by piece and removing solutions that fail to satisfy the constraints of the problem. It's often used in situations where you need to explore all possible combinations or permutations to find the correct one(s).

  In simply we can say: It recursively builds paths for the solutions and abandons a path (backtracks) as soon as it determines that it can't lead to a solution.

  • Choose: Make a choice to add an element to the current solution.
  • Explore: Recursively attempt to build solution by making further choices.
  • Un-choose (Backtrack): If the current path does not lead to a valid solution, undo the last choice and try other possibilities.

Pros and Cons of Recursion

Pros:

1. Simplifies Code: Problems that have a repetitive structure can be written more concisely with recursion.
2. Elegant Solutions: Recursive solutions are often cleaner and more intuitive for problems like tree traversals, permutations, and combinatorics.
3. Divide and Conquer: Recursion is useful in algorithms like merge sort, quicksort, and divide-and-conquer strategies.

Cons:

1. Stack Overflow: Each recursive call adds a new frame to the call stack. If the recursion goes too deep (especially without a proper base case), it can lead to a stack overflow.
   1. Each function call consumes a certain amount of memory on the stack. This memory includes parameters, local variables, and the return address. When a function calls itself recursively without reaching the base case or without proper termination conditions, it keeps adding new stack frames, eventually exhausting the available stack space.
2. Slower Performance: Recursion can be less efficient in terms of time and space due to repeated function calls and memory overhead.
3. Hard to Debug: Understanding the flow of recursion can be more complex than iterative solutions.

Tips and Tricks to Solve Any Recursion Problem

Recursion is applied in situations where we have choices and need to make decisions on the basis of those choices.

choices + decision = recursion

🤔Does we make input smaller in recursion ?

In recursion we don't aim to make input smaller, we aim for decision making and as a result input automatically reduces to smaller version of itself.

Primary goal is decision making and side product is smaller input.

Each recursive call represents a choice or a decision about how to handle the current part of the problem.

The recursive function often needs to decide what to do next based on the current state of the input (such as splitting an array, moving to the next element, etc.).

Example:

In merge sort, the primary goal is not directly to reduce the size of the input but to decide how to split the array and then merge the results:

void mergeSort(vector<int>& arr, int left, int right) {
    // Base case: If the array has one or zero elements, it's already sorted
    if (left >= right) {
        return;
    }

    // Decision: Split the array into two halves
    int mid = left + (right - left) / 2;

    // Recursive case: Sort the two halves
    mergeSort(arr, left, mid);
    mergeSort(arr, mid + 1, right);

    // Decision: Merge the sorted halves
    merge(arr, left, mid, right);
}

In this case:

• Primary goal: The decisions involve splitting the array and merging the sorted halves.
• Side effect: The input size reduces as part of the decision to split the array in half.

Example:

For Fibonacci numbers, the primary goal is to decide the relation between Fib(n) and Fib(n-1) and Fib(n-2):

int fibonacci(int n) {
    // Base case: Return n if it's 0 or 1
    if (n == 0 || n == 1) {
        return n;
    }
    
    // Decision: Calculate Fibonacci of n-1 and n-2
    return fibonacci(n - 1) + fibonacci(n - 2);
}

Here:

• Primary goal: The decision to return Fib(n-1) + Fib(n-2) based on the structure of the problem.
• Side effect: The input (n) decreases as you make that decision.

1. Identify the Base Case

The base case is the simplest version of the problem, where no further recursion is required. It tells the function when to stop calling itself and prevents infinite recursion. This is the condition that will stop the recursive calls.

• Ask yourself: "When do I want the recursion to stop?"
• The base case is often the smallest or trivial instance of the problem.
• A well-defined base case simplifies the problem and helps you avoid stack overflow errors.

Example:

In a factorial problem, the base case is factorial(0) = 1. Since 0! is 1.

if (n == 0) // Base Case
    return 1;

2. Determine the Recursive Case

The recursive case is the part where you reduce the problem size and call the function recursively. The goal is to reduce the problem in every step, leading closer to the base case.

• Decompose the problem into smaller subproblems.
• Each recursive call should get closer to the base case.
• Recursive Case solves the problem by calling the function itself with a smaller input.
• Break the problem into smaller chunks until you reach the base case.

Tip: Focus on how each step can lead you closer to the base case.

Example:

For the factorial problem, the recursive case is n! = n * (n-1)!.

// Recursive case

return n * factorial(n - 1);  // Recursive case

3. Think of Recursion as a Function Stack

When solving recursion problems, remember that each function call is added to a stack, and the problem is solved from the bottom of the stack as it unwinds.

• The function calls are stacked, and once the base case is reached, the stack unwinds, returning the results back to previous function calls.
• This can help you understand how intermediate values are returned.
• Every recursive call pushes a new frame onto the stack with its own arguments and local variables.
• Once the base case is reached, the function returns and starts popping frames off the stack, backtracking to solve the original problem.
• Tip: Visualize the recursive calls like a stack. Each recursive call "pauses" until the base case is hit, and then the function resumes as the stack unwinds.

4. Write Recursive Code from Base to Recursive Case

• When designing a recursive solution, start by defining the base case first.
• Then, think about how the recursive call should behave to approach that base case.
• Tip: Break the problem down and focus on how to handle smaller instances of the problem after the base case is established.

Example:
For summing an array:

• Base Case: If the array has one element, return that element.
• Recursive Case: Otherwise, return the sum of the first element and the sum of the rest of the array.

int sumArray(int arr[], int n) {
    if (n == 1) 
        return arr[0];  // Base case
    return arr[0] + sumArray(arr + 1, n - 1);  // Recursive case
}

5. Beware of Stack Overflow (Deep Recursion)

Recursion comes with a risk of stack overflow if the depth of recursion is too large. This happens because each recursive call adds a new frame to the stack, and a deep recursion can exhaust the stack memory.

• In such cases, consider optimizing recursion or using an iterative solution.
• Use techniques like tail recursion or limit the depth of recursion if possible.

Tail Recursion Optimization:

Tail recursion is a special case of recursion where the recursive call is the last action in the function. Some compilers can optimize tail recursion to prevent stack overflow by reusing the current stack frame.

• Tail recursion occurs when the recursive call is the last action in the function. Some compilers optimize tail-recursive functions by reusing the current function’s stack frame instead of adding a new one.
• Tip: Convert your recursion to tail recursion whenever possible to improve performance.

Example:
Regular factorial recursion vs. tail-recursive factorial:

Regular recursion:

int factorial(int n) {
    if (n == 0) return 1;
    return n * factorial(n - 1);
}

Tail recursion:

int factorialTail(int n, int result = 1) {
    if (n == 0) return result;
    return factorialTail(n - 1, n * result);  // Tail recursive
}

6. Edge | Corner Cases

Always handle the edges cases like:

• n = 0
• n = 1
• and much more.

Recursion Tree

A recursion tree is a visual representation used to understand how recursive algorithms break down a problem into smaller subproblems. It helps in visualizing the steps of a recursive function and analyzing its time complexity. Recursion trees are especially useful in dynamic programming, divide and conquer algorithms, and understanding recurrence relations.

A recursion tree is a visual representation that helps understand the flow of recursive calls. It shows how the problem is divided into smaller subproblems at each recursive step.

Key Components of a Recursion Tree

1. Root Node: Represents the initial call to the recursive function. This is the largest problem size you're solving.
2. Branches: Represent the recursive calls made by the function. Each branch shows how the function breaks the problem down into smaller subproblems.
3. Leaf Nodes: These are the base cases of the recursion, where the function stops making recursive calls.

Recursion Tree in both types:

1. Recursion Tree for Head Recursion:

In head recursion, the tree grows downward as the function waits for each recursive call to complete before executing the remaining operations.

2. Recursion Tree for Tail Recursion:

In tail recursion, the recursion tree is simpler since each recursive call is the last operation, leading to more straightforward unwinding of the stack.

Recursion Tree for Fibonacci

Consider the recursive Fibonacci function:

int fib(int n) {
    if (n <= 1)
        return n;
    return fib(n-1) + fib(n-2);
}

The recursion tree for fib(4) would look like:

           fib(4)
          /      \
      fib(3)    fib(2)
      /   \      /   \
 fib(2) fib(1) fib(1) fib(0)
  /  \
fib(1) fib(0)

Here, you can see that many calls to fib(n) are repeated, leading to an exponential time complexity. This visualization highlights the inefficiency of naive recursion for Fibonacci.

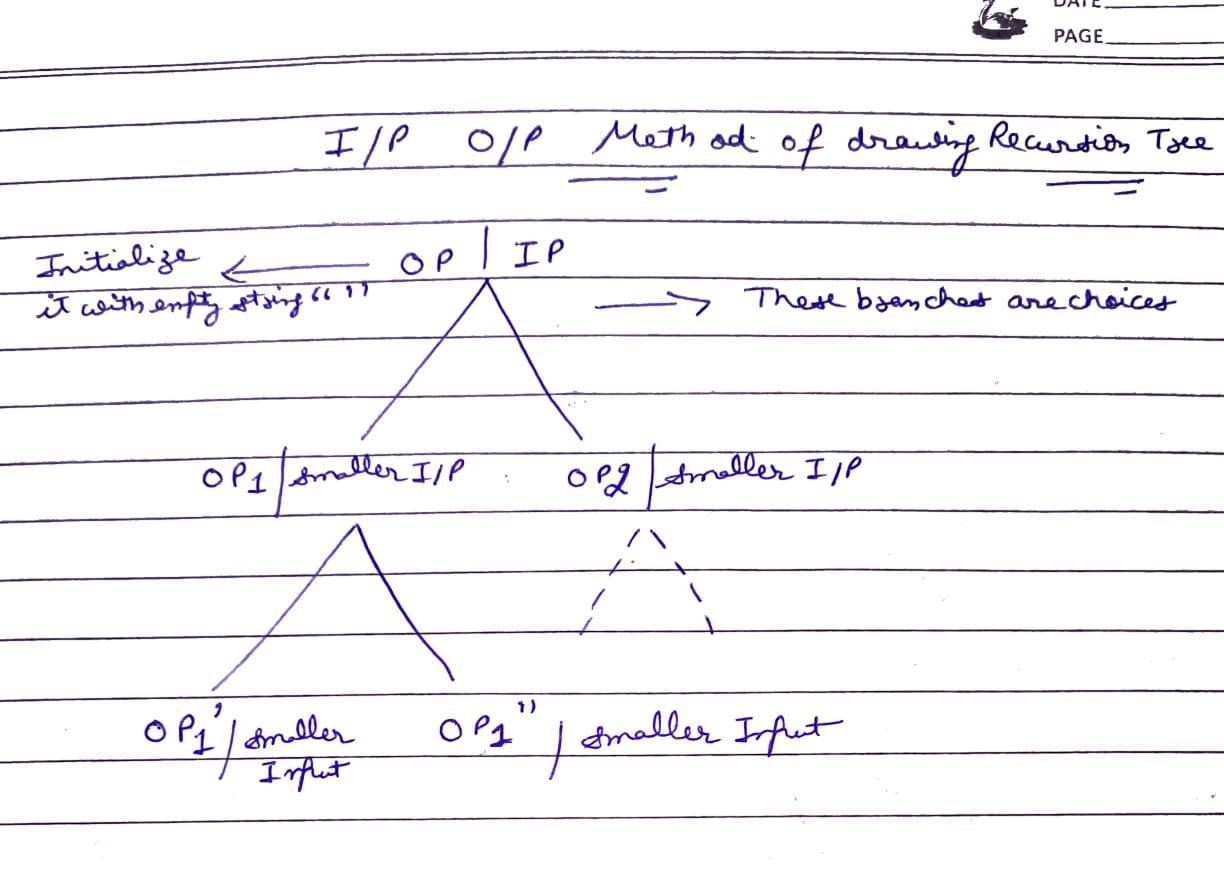
Input/Output method of drawing recursion tree :-

The input-output method of a recursion tree is a visual way to understand the decision-making process in recursion, where each recursive call is represented as a node in the tree. This method helps break down how recursion makes decisions, how input is transformed, and how the output is generated step by step.

Key Concepts of Input-Output Method:

1. Input: This is the data or problem you're passing to the recursive function at each step.
2. Output: This is the result you're expecting from that recursive call.
3. Recursive Calls: At each recursive step, the problem is divided into smaller subproblems, and new recursive calls are made with smaller inputs.
4. Tree Representation: The recursion tree branches out at each decision point, showing how the recursive function splits into different possibilities (or recursive calls).

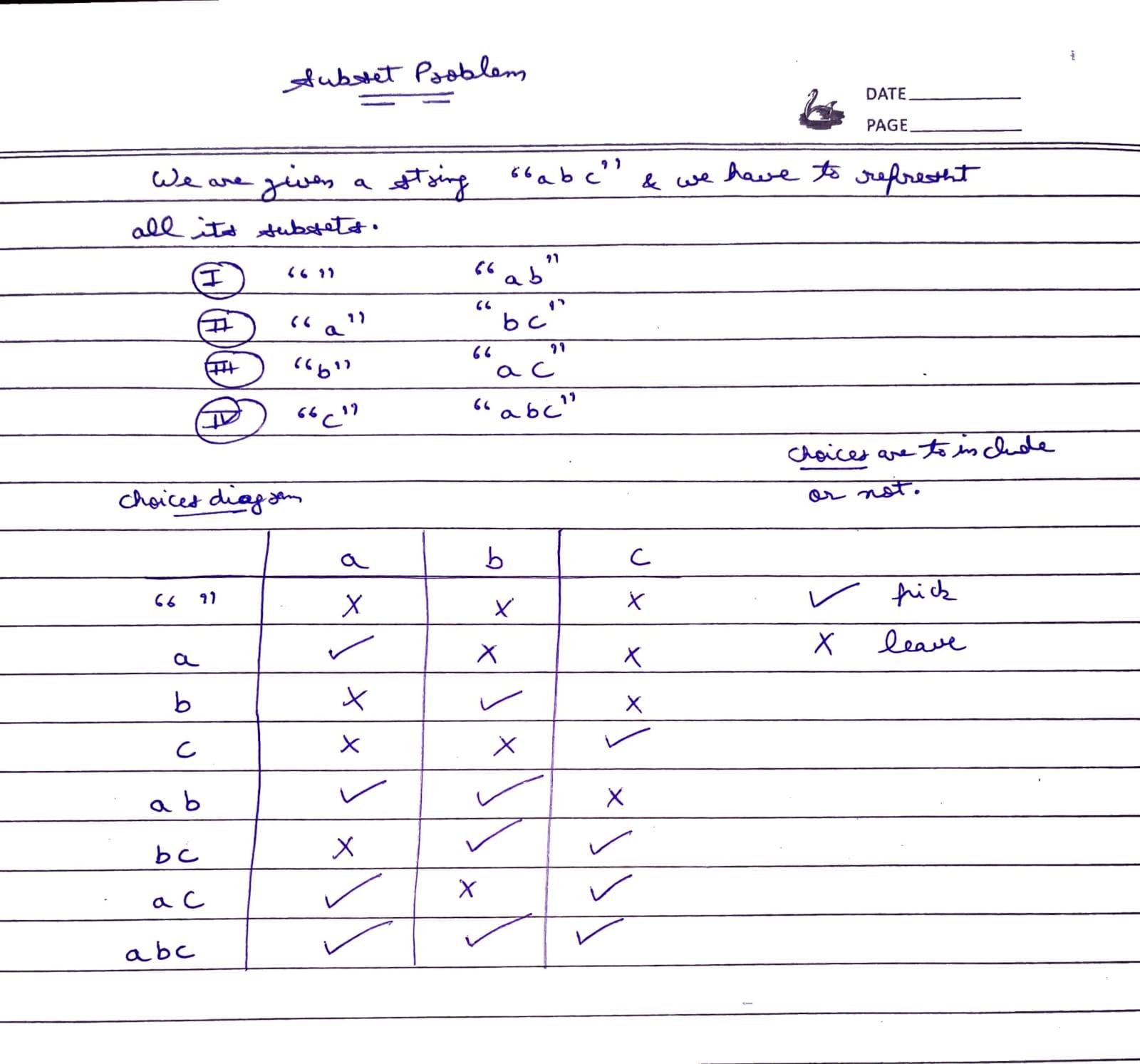
We’ll use the input-output method to generate subsets of the string "abc" recursively.

Recursive Function:

The function takes two parameters:

• Input: The remaining characters in the string.
• Output: The subset formed so far.

For each character in the string, you have two choices:

1. Include the character in the subset.
2. Exclude the character from the subset.

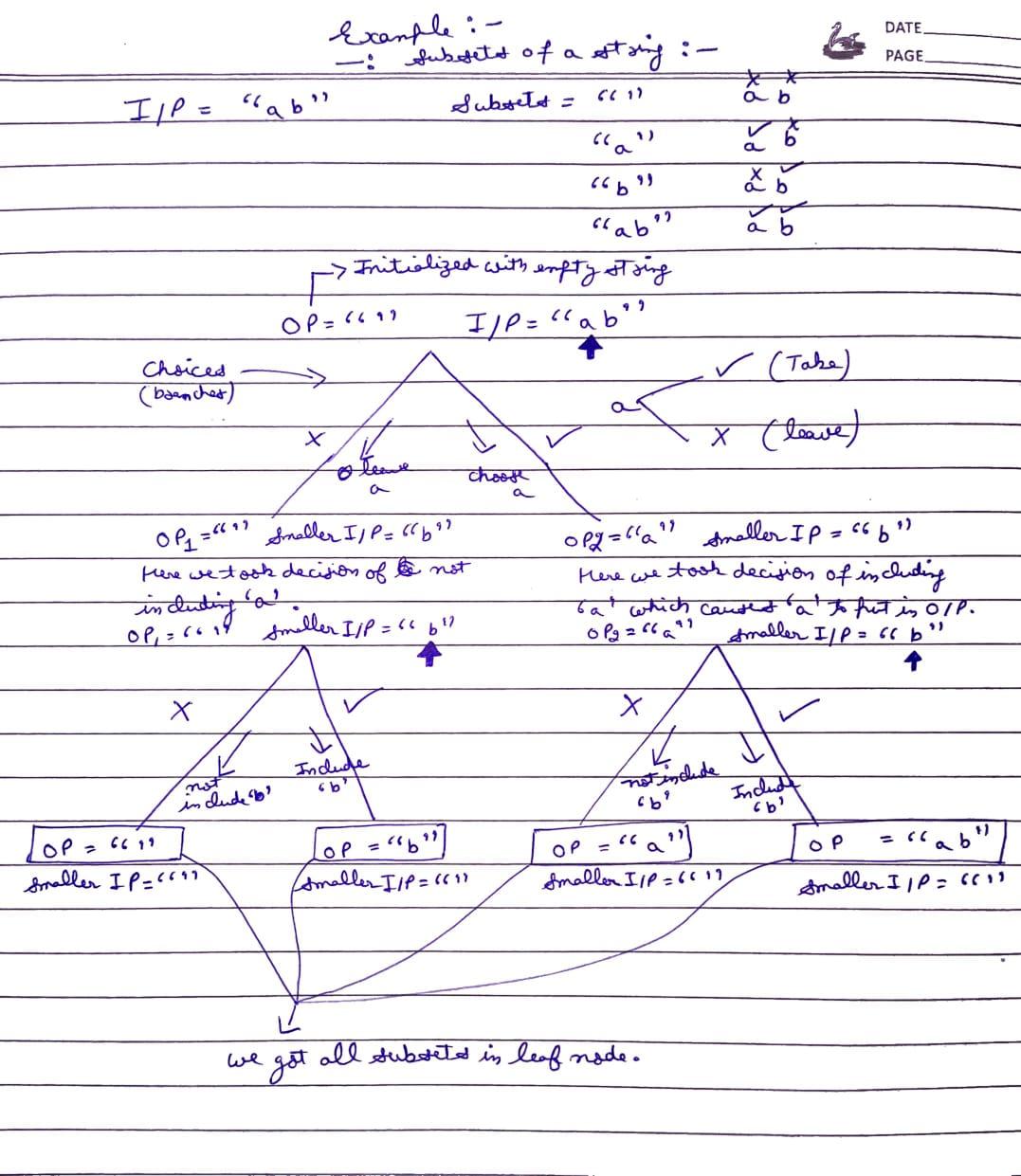
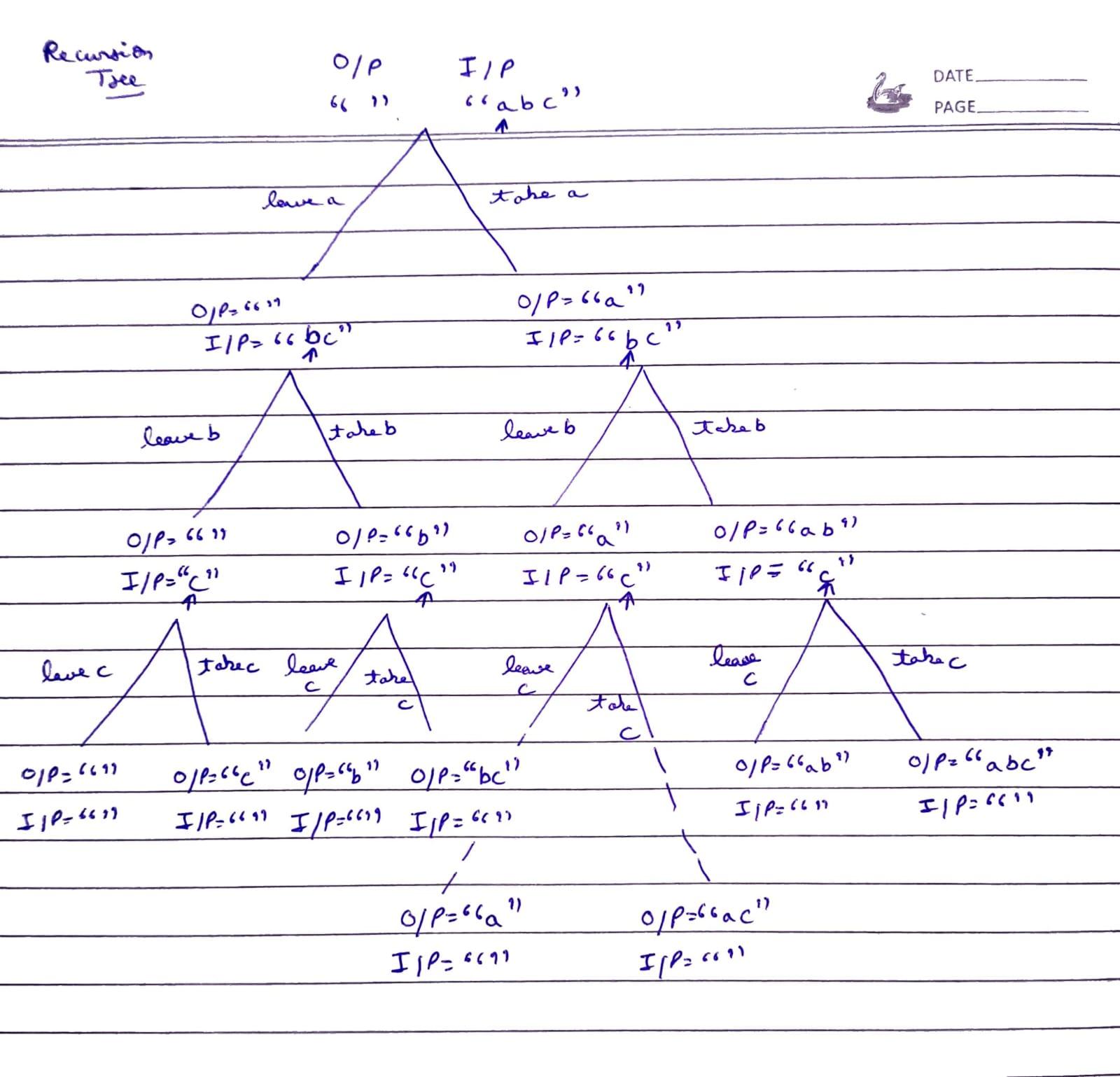
Let's break down the recursion tree for generating subsets of the string "ab" using the same method. At each level, the function decides whether to include or exclude each character in the subset.

Level 0 (Initial Call):

• Input: "ab"
• Output: "" (initially, the subset is empty)

Two recursive calls are made:

1. Exclude "a", call the function with input "b" and output "".
2. Include "a", call the function with input "b" and output "a".

Level 1:

• First Call: Input = "b", Output = ""
• Second Call: Input = "b", Output = "a"

For each of these calls, again two decisions are made: exclude or include the character "b".

Level 2:

1. First Call: Input = "", Output = "" (exclude "b")
   • Exclude "b", call with input "", output "".
   • Include "b", call with input "", output "b".
2. Second Call: Input = "", Output = "a" (include "a")
   • Exclude "b", call with input "", output "a".
   • Include "b", call with input "", output "ab".

Level 3 (Base Case):

At this level, the input string is empty (""), and you have your final outputs (subsets). Each recursive branch returns its subset.

Here’s the complete recursion tree with input-output transformations:

                ("ab", "")
               /         \
         ("b", "")       ("b", "a")
        /       \        /       \
    ("", "")  ("", "b")("", "a") ("", "ab")

The outputs of these recursive branches are:

• "" (empty set)
• "b"
• "a"
• "ab"

Tail Recursion

Tail recursion is a special case of recursion where the recursive call is the last operation in the function. This means that once the recursive call is made, there’s nothing left to do in the current function except return the result of the recursive call. Because of this structure, tail recursion can be optimized by some compilers or interpreters to avoid using additional stack frames, a technique called tail call optimization (TCO).

Key Characteristics of Tail Recursion

1. Last Operation: The recursive call must be the last operation in the function. No additional operations (e.g., additions or multiplications) should follow the recursive call.
2. Stack Optimization: In tail-recursive functions, since there is no need to keep track of the previous state once a recursive call is made, the compiler can reuse the current stack frame for the next call, reducing the risk of a stack overflow for deep recursion.

Example of Non-Tail Recursion (Factorial)

A standard recursive factorial function is not tail-recursive because the multiplication happens after the recursive call:

int factorial(int n) {
    if (n == 0 || n == 1)
        return 1;
    return n * factorial(n - 1);  // Multiplication occurs after the recursive call
}

In this case, the recursive call to factorial(n - 1) happens first, but the function still needs to multiply the result by n after the recursion returns. As a result, the state of each recursive call must be preserved until the final multiplication, which uses up stack space.

Example of Tail Recursion (Tail-Recursive Factorial)

In a tail-recursive version of the factorial function, the recursive call is the last thing that happens, and the result is passed along in an accumulator. This allows the compiler to optimize the recursion by not needing to retain the previous state.

int factorialHelper(int n, int accumulator) {
    if (n == 0 || n == 1)
        return accumulator;
    return factorialHelper(n - 1, n * accumulator);  // Tail recursion
}

int factorial(int n) {
    return factorialHelper(n, 1);
}

In this version, the multiplication happens as part of the argument in the recursive call, and the recursion passes down the accumulated result (accumulator). The recursive call is now the last operation, making it tail-recursive.

Tail Recursion vs. Non-Tail Recursion

• Tail Recursion:
  • Recursive call is the last operation.
  • Can be optimized to avoid deep stack usage (via TCO).
  • Often needs an extra parameter (accumulator) to hold intermediate results.
• Non-Tail Recursion:
  • Additional operations occur after the recursive call.
  • Cannot be optimized as easily since the current state needs to be preserved.
  • Risk of stack overflow for very deep recursion.

Tail Call Optimization (TCO)

Many modern compilers and interpreters (like GCC and Clang for C++) can perform tail call optimization, where the stack frame for the current recursive call is reused for the next call. This makes tail-recursive functions effectively iterative, with constant space complexity (O(1)), unlike non-tail recursive functions, which typically have space complexity proportional to the depth of the recursion (O(n)).

For example, with tail recursion:

• Time Complexity: O(n)
• Space Complexity: O(1) (due to TCO)

Without tail recursion:

• Time Complexity: O(n)
• Space Complexity: O(n) (each recursive call adds a new stack frame)

Types of Recursion

1️⃣ Head Recursion:

In head recursion, the recursive call occurs before any other processing in the function. The function waits for the recursive call to return before proceeding with any operation.

Example: The following code prints number from 1 to 5 using head recursion.

// C++ Example of Head Recursion
#include <iostream>
using namespace std;

void headRecursion(int n) {
    if (n > 0) {
        headRecursion(n - 1);  // Recursive call before processing
        cout << n << " ";  // Processing after recursion
    }
}

int main() {
    headRecursion(5);
    return 0;
}

2️⃣ Tail Recursion:

In tail recursion, the recursive call is the last operation in the function. Once the function calls itself, there is no need to retain the current function's state, allowing the compiler to optimize tail recursion.

Example: The following code prints number from 5 to 1 using tail recursion.

// C++ Example of Tail Recursion
#include <iostream>
using namespace std;

void tailRecursion(int n) {
    if (n == 0)
        return;
    cout << n << " ";  // Processing before recursion
    tailRecursion(n - 1);  // Recursive call is the last action
}

int main() {
    tailRecursion(5);
    return 0;
}

Complexity Analysis:

• Time Complexity
  • The time complexity of a recursive function is generally based on the number of recursive calls made. If a function makes one recursive call, the time complexity is O(n), where n is the depth of the recursion.
• Space Complexity
  • The space complexity of a recursive function is determined by the maximum depth of the recursive call stack. If the function reaches a maximum recursion depth of n, the space complexity is O(n).

Some Terms

Stack Frame:

In a recursive function, each function call creates a new instance of a stack frame on the call stack. This stack frame is independent of the previous one, even though it belongs to the same function. When a function is called, the program pushes a new stack frame onto the call stack, and when the function finishes, the stack frame is popped off the stack.

Key components of a stack frame:

1. Function parameters: The values passed to the function.
2. Return address: The location in the code where execution should return after the function completes.
3. Local variables: Variables declared inside the function.
4. Saved registers: Certain CPU registers that must be preserved across function calls.

Winding and Unwinding:

In recursion, winding refers to the process of pushing stack frames onto the call stack as the recursive calls progress deeper. Unwinding refers to the process of popping those stack frames off the stack as the recursive calls return.

Winding:

• During the recursive calls, new stack frames are pushed onto the call stack.
• Each recursive call pauses execution at that point until the recursive sub-call completes.
• The function continues to "wind up" until a base case is reached, which signals the end of the recursion.

Unwinding:

• Once the base case is reached, the recursive calls begin to return.
• As each function call completes, its stack frame is popped off the call stack, and the function resumes execution from where it was paused.
• The function continues to "unwind" until the initial function call is completed.

Base Condition, Hypothesis and Induction

1️⃣ Base Condition:

The base condition is the stopping point of the recursion, defining when the function should return a result a without making further recursive calls.

It is the smallest valid or invalid input possible.

Without a base condition, the function would call itself indefinitely, causing a stack overflow.

Example: In a factorial function, the base condition is if n == 0: return 1, because 0! = 1.

2️⃣ Hypothesis:

The hypothesis is the assumption that the recursive function correctly solves smaller instances of the problem.

It allows us to assume that our function works for a smaller input, which helps in defining the recursive solution..

Example: In the factorial for n, assume factorial(n - 1) gives the correct factorial for n - 1.

3️⃣ Induction:

The induction step uses the result of the hypothesis (the smaller subproblem) to solve the current problem instance.

It completes the recursive logic by combining the results from smaller instances to obtain the final solution.

Example: In the factorial function, factorial(n) = n * factorial(n-1) uses factorial(n - 1) from the hypothesis to find factorial(n).

Example:

Ways to Solve Recursion Problem

1️⃣ Recursion Tree I/P O/P Method:

The Recursion Tree or Input/Output Method is particularly helpful when you are given choices in the problem. Here, you visualize each recursive call as a branching decision tree that represents possible states or actions based on those choices.

How It Works

• Identify the Choices: Start by identifying the choices available at each stage of the problem (e.g., whether to include/exclude an item, take a left/right path, etc.).
• Base Case: Set up a base case to stop recursion when no further choices or actions are left.
• Recursive Tree: Map out each recursive call as a branching decision in the tree, where each branch represents a choice or action.
• Track Input and Output: Use parameters to keep track of the current input and output states so you can pass them to the next recursive call.

When to Use It

• Use the Recursion Tree approach when:
  • You are making decisions at each recursive step.
  • You need to explore all possible outcomes (such as in backtracking).
  • The problem involves combinations, permutations, subsets, or any other scenarios where multiple choices lead to different results.

Example: Generating All Subsets of a Set

In a subset generation problem, you decide at each step whether to include or exclude an element from the subset, forming a decision tree with each call branching into two choices.

2️⃣ IBH - Induction, Base Case, Hypothesis:

The IBH (Induction, Base Case, Hypothesis) approach is useful for problems where you don’t have explicit choices but need to break down the input into smaller parts. This method is especially effective when the problem requires reducing the input size progressively until you reach a minimal case.

How It Works

• Base Case: Identify the simplest form of the problem that can be solved without further recursion. Smallest valid input possible.
• Hypothesis: Assume that your recursive function works correctly for a smaller input.
• Induction Step: Using the hypothesis, build up the solution for the original problem by solving the smaller problem and combining it with the current element or state.

When to Use It

• Use IBH when:
  • You don’t have explicit choices at each recursion level.
  • The problem can be reduced to a smaller instance (e.g., factorial, Fibonacci series, reversing a list).
  • The recursive structure involves transforming or reducing the input until a base case is reached, rather than making choices.

Example: Calculating Factorial

In a factorial calculation, you assume that the function correctly calculates factorial (n-1), and then use the result to calculate n * factorial (n-1).

When to Use Backtracking?

Use backtracking when asked about: All possible Permutations | Combinations | Subsets | Subsequences.

References

1. https://leetcode.com/discuss/study-guide/1733447/become-master-in-recursion
2. https://leetcode.com/discuss/study-guide/2244368/backtracking-for-beginners-problems