Problem Statement
You are given an n x n grid representing a field of cherries, each cell is one of three possible integers.
- 0 means the cell is empty, so you can pass through,
- 1 means the cell contains a cherry that you can pick up and pass through, or
- -1 means the cell contains a thorn that blocks your way.
Return the maximum number of cherries you can collect by following the rules below:
- Starting at the position (0, 0) and reaching (n - 1, n - 1) by moving right or down through valid path cells (cells with value 0 or 1).
- After reaching (n - 1, n - 1), returning to (0, 0) by moving left or up through valid path cells.
- When passing through a path cell containing a cherry, you pick it up, and the cell becomes an empty cell 0.
- If there is no valid path between (0, 0) and (n - 1, n - 1), then no cherries can be collected.
Examples
Example 1:
Input: grid = [[0,1,-1],[1,0,-1],[1,1,1]]
Output: 5
Explanation: The player started at (0, 0) and went down, down, right right to reach (2, 2).
4 cherries were picked up during this single trip, and the matrix becomes [[0,1,-1],[0,0,-1],[0,0,0]].
Then, the player went left, up, up, left to return home, picking up one more cherry.
The total number of cherries picked up is 5, and this is the maximum possible.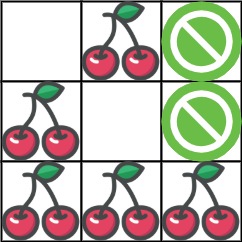
Example 2:
Input: grid = [[1,1,-1],[1,-1,1],[-1,1,1]]
Output: 0Different Approaches
1️⃣ Recursive Approach
Intuition:
The question clearly states that the path which we traverse will be rejected and another path will be traversed to maximize the no. of cherries during homecoming to (0,0) . Now when we dry run this statement in the following pictogtaphic dry run
- When Person moves from (0,0) -> (2,2) with moves
- Down -> Down -> Right -> Right
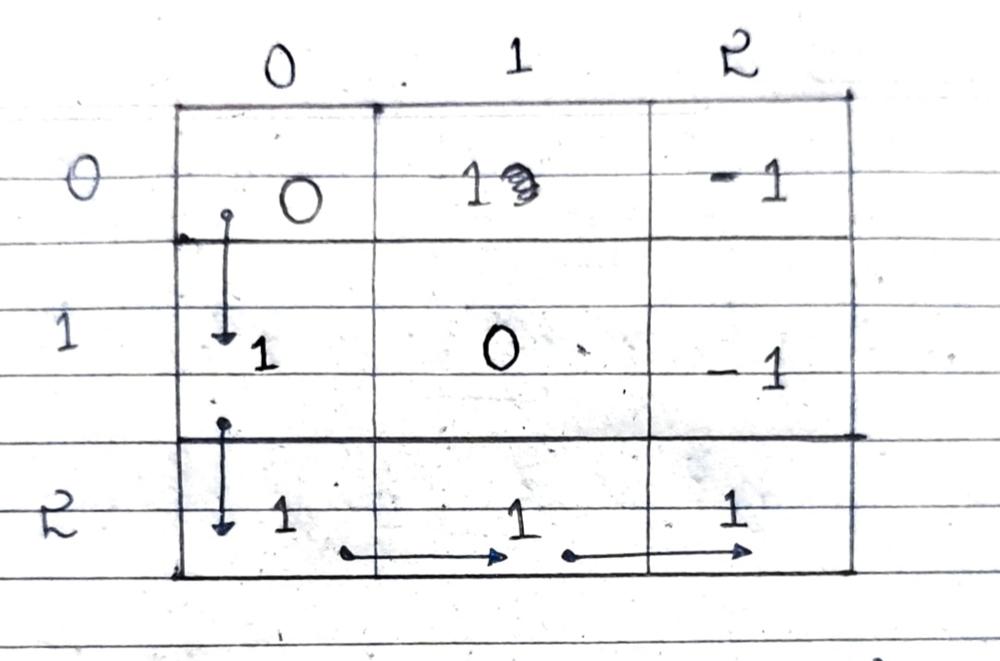
- When Person moves from (2,2) -> (0,0) with moves
- Left -> Up -> Up -> Left
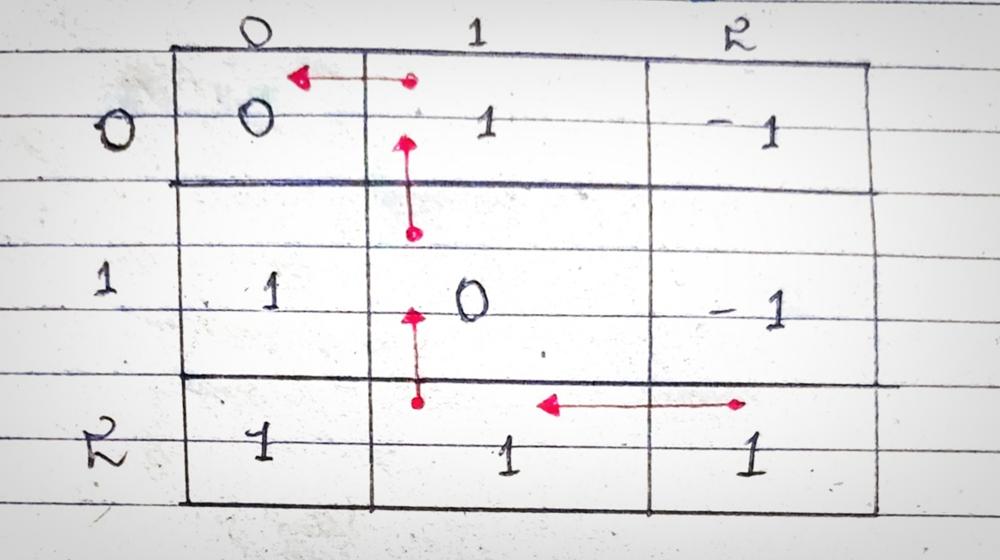
- These 2 dry runs when combined into one will look like this:
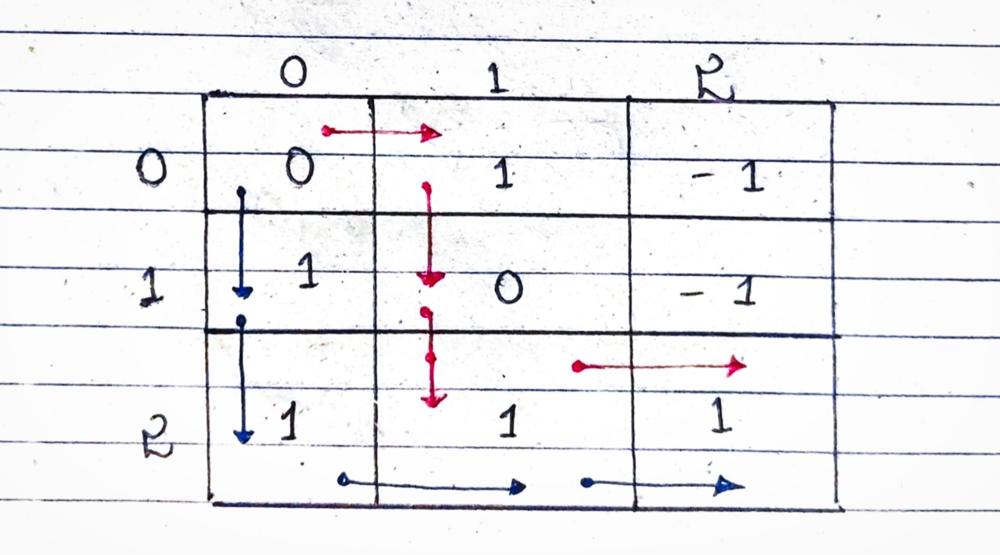
the combined dry run -> looks like two different people walking from the same starting point towards (n-1,n-1) while covering up cherries in their maximized way.
- Notice that when they encounter the same cell that is (2,1) the cherry is only added once that is because the first person would have taken that cherry earlier during traversal.
Code:
#include <bits/stdc++.h>
using namespace std;
class Solution {
private:
// Recursive function to calculate maximum cherries
int dfs(int r1, int c1, int r2, vector<vector<int>> &grid, int n) {
int c2 = r1 + c1 - r2; // Calculate c2 from r1, c1, and r2
// Base case: Out of bounds or thorn cell
if (r1 >= n || c1 >= n || r2 >= n || c2 >= n ||
grid[r1][c1] == -1 || grid[r2][c2] == -1) {
return -1e9; // Invalid path
}
// Base case: Both agents reach bottom-right cell
if (r1 == n - 1 && c1 == n - 1) {
return grid[r1][c1];
}
// Collect cherries from both agents
int cherries = grid[r1][c1];
if (r1 != r2 || c1 != c2) {
cherries += grid[r2][c2];
}
// Explore all combinations of moves
int maxCherries = max({
dfs(r1 + 1, c1, r2 + 1, grid, n), // Both move down
dfs(r1, c1 + 1, r2, grid, n), // Agent 1 right, Agent 2 down
dfs(r1 + 1, c1, r2, grid, n), // Agent 1 down, Agent 2 right
dfs(r1, c1 + 1, r2 + 1, grid, n) // Both move right
});
return cherries + maxCherries;
}
public:
int cherryPickup(vector<vector<int>>& grid) {
int n = grid.size();
return max(0, dfs(0, 0, 0, grid, n)); // Start from top-left
}
};
int main() {
vector<vector<int>> grid = {
{0, 1, -1},
{1, 0, -1},
{1, 1, 1}
};
Solution sol;
cout << sol.cherryPickup(grid) << endl; // Output: 5
return 0;
}
Complexity Analysis:
- Time Complexity:
O(4 ^(n^2))(Exponential due to exploring all paths). - Space Complexity:
O(n^2)for recursion stack.
