Problem Statement

Given a 2D array matrix where each row is sorted in ascending order from left to right and each column is sorted in ascending from top to bottom. Find the specific integer target in the matrix.

Examples

Example 1:

Input: matrix = [
                 [1, 4, 7, 11, 15],
                 [2, 5, 8, 12, 19],
                 [3, 6, 9, 16, 22],
                 [10, 13, 14, 17, 24],
                 [18, 21, 23, 26, 30],
                ],
                target = 5
Output: True

Explanation: The target 5 exists in the matrix at the index (1, 1).

Example 2:

Input: matrix = [
                 [1, 4, 7, 11, 15],
                 [2, 5, 8, 12, 19],
                 [3, 6, 9, 16, 22],
                 [10, 13, 14, 17, 24],
                 [18, 21, 23, 26, 30],
                ],
                target = 20
Output: True

Explanation: The target 20 does not exists in the matrix.

Different Approaches

1️⃣ Brute Force Approach

Intuition:

Use the linear search to iterate through the matrix row wise and look for the target. It is similar to the one we use in the problem, search in 2D matrix - 1.

2️⃣ Better Approach

Intuition:

Since the given matrix is sorted (both row-wise and column-wise), this information can be used to optimize the brute-force solution. The brute-force approach involves checking each cell of the matrix for the given target, similar to how it was done in the problem Search in 2D matrix. Here, to optimize the solution, use binary search in each row of the matrix to search for the target. If the target is found return true, else return false.

Approach:

Working of searchMatrix(matrix, target):

1. Traverse each row of the matrix using a for loop.
2. Next, for every row, check if it contains the target using binary search.
3. After applying binary search on the row, if the target is found, return true. Otherwise, move on to the next row, as the target might be present there.
4. Finally, after completing all the row traversals, if no matching element is found, return false.

Working of binarySearch(arr, target):

1. First initialize low to 0 and and high to the last column index. This will define the search range of the binary search.
2. While low is less than or equal to high, calculate 'mid' and check if the element at mid is equal to target, if so, return true. Otherwise, if element at mid is greater than target, eliminate the right half, else eliminate the left half.

Code:

#include <bits/stdc++.h>
using namespace std;

class Solution {
private:
    //Helper function to perform binary search
    bool binarySearch(vector<int>& nums, int target) {
        int n = nums.size(); 
        int low = 0, high = n - 1;

        // Perform the steps:
        while (low <= high) {
            int mid = (low + high) / 2;
            
            //Return true if target is found
            if (nums[mid] == target) return true;
            else if (target > nums[mid]) low = mid + 1;
            else high = mid - 1;
        }
        //Return false if target not found
        return false;
}
public:
    //Function to search for a given target in matrix
    bool searchMatrix(vector<vector<int>>& matrix, int target) {
        int n = matrix.size();
        int m = matrix[0].size();
        
        //Traverse through each row
        for (int i = 0; i < n; i++) {
            
            /*Check if target is 
            present in the current row*/
            bool flag =  binarySearch(matrix[i], target);
            
            if (flag) return true;
        }
        // Return false if target is not found
        return false; 
    }
};

int main() {
    
    vector<vector<int>> matrix = {{1, 4, 7, 11, 15}, 
                                  {2, 5, 8, 12, 19},
                                  {3, 6, 9, 16, 22},
                                  {10, 13, 14, 17, 24},
                                  {18, 21, 23, 26, 30}};
    int target = 8;
    
    //Create an instace of Solution class
    Solution sol;
    
    bool result = sol.searchMatrix(matrix, target);
    
    // Output the result
    result ? cout << "true\n" : cout << "false\n";
    
    return 0;
}

Complexity Analysis:

• Time Complexity: O(N * logM), where N is the number of rows in the matrix, M is the number of columns in each row. All rows are traversed in O(N) time complexity, and binary search is applied to each row. Therefore, the total time complexity is O(N*logM).
• Space Complexity: As no additional space is used, so the Space Complexity is O(1).

3️⃣ Optimal Approach

Intuition:

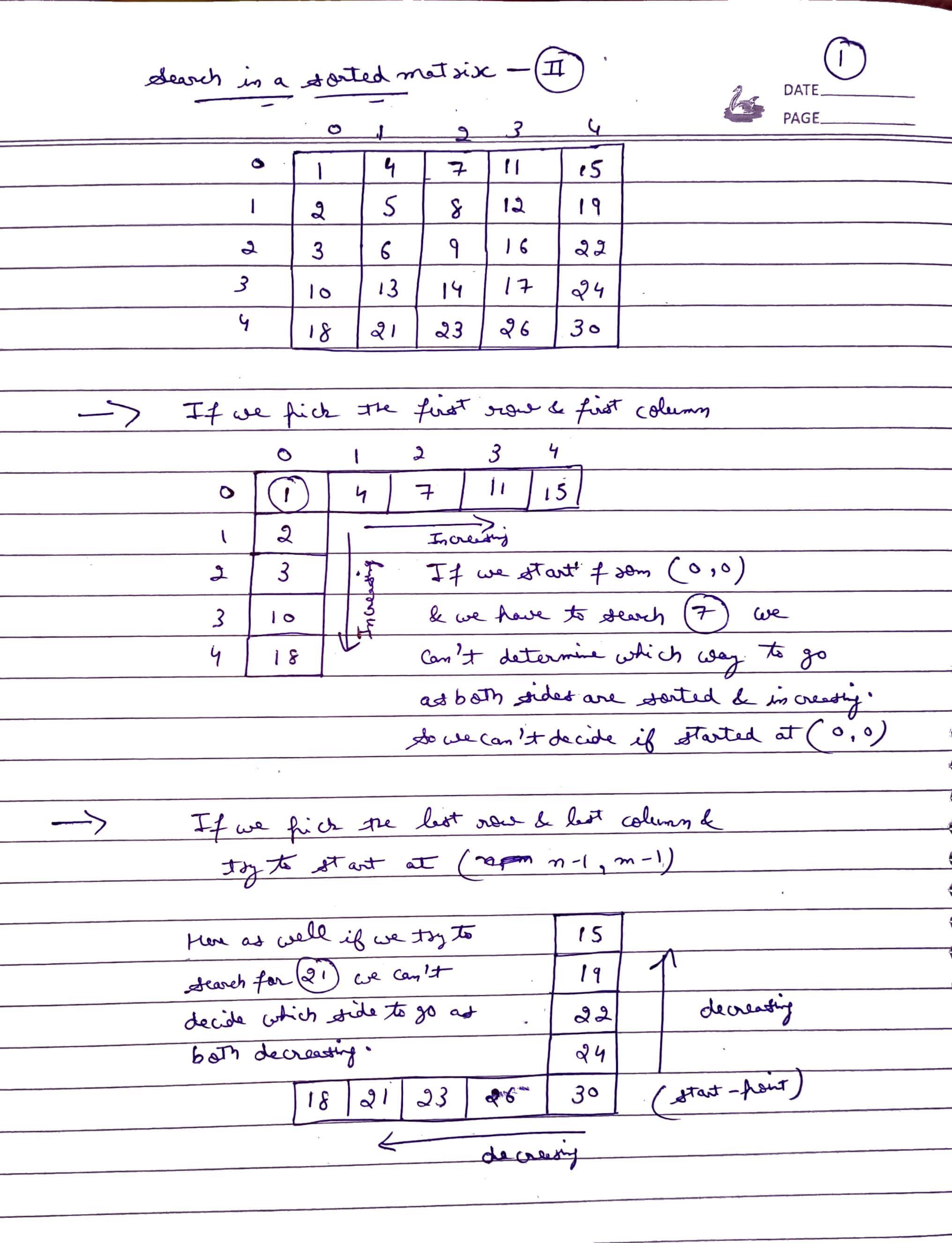
• Here, the idea is to utilize the information that the matrix is sorted both row-wise (increasing from left to right) and column-wise (increasing from top to bottom). One corner of the matrix is chosen from (0, 0), (0, m-1), (n-1, 0), and (n-1, m-1). This selection ensures that moving in one direction (either vertically or horizontally) from this corner will lead only to smaller elements, while moving in the other direction will lead only to larger elements relative to the element at the chosen corner.
• This strategy enhances traversal efficiency: if the element at the corner is smaller than the target, move in the direction where larger elements are present; if the element at the corner is greater than the target, move in the direction where smaller elements are present. If neither condition applies, it indicates that the corner element is the target, and true should be returned.

How to choose starting corners:

• Assume n is the row number and m is the number of columns in each row.
• Cell (0, 0): Assume traversal starts from (0, 0) and the search target is 14. Since both the row and column are sorted in increasing order, it cannot be determined whether to proceed row-wise or column-wise. Therefore, traversal cannot be started from (0, 0).
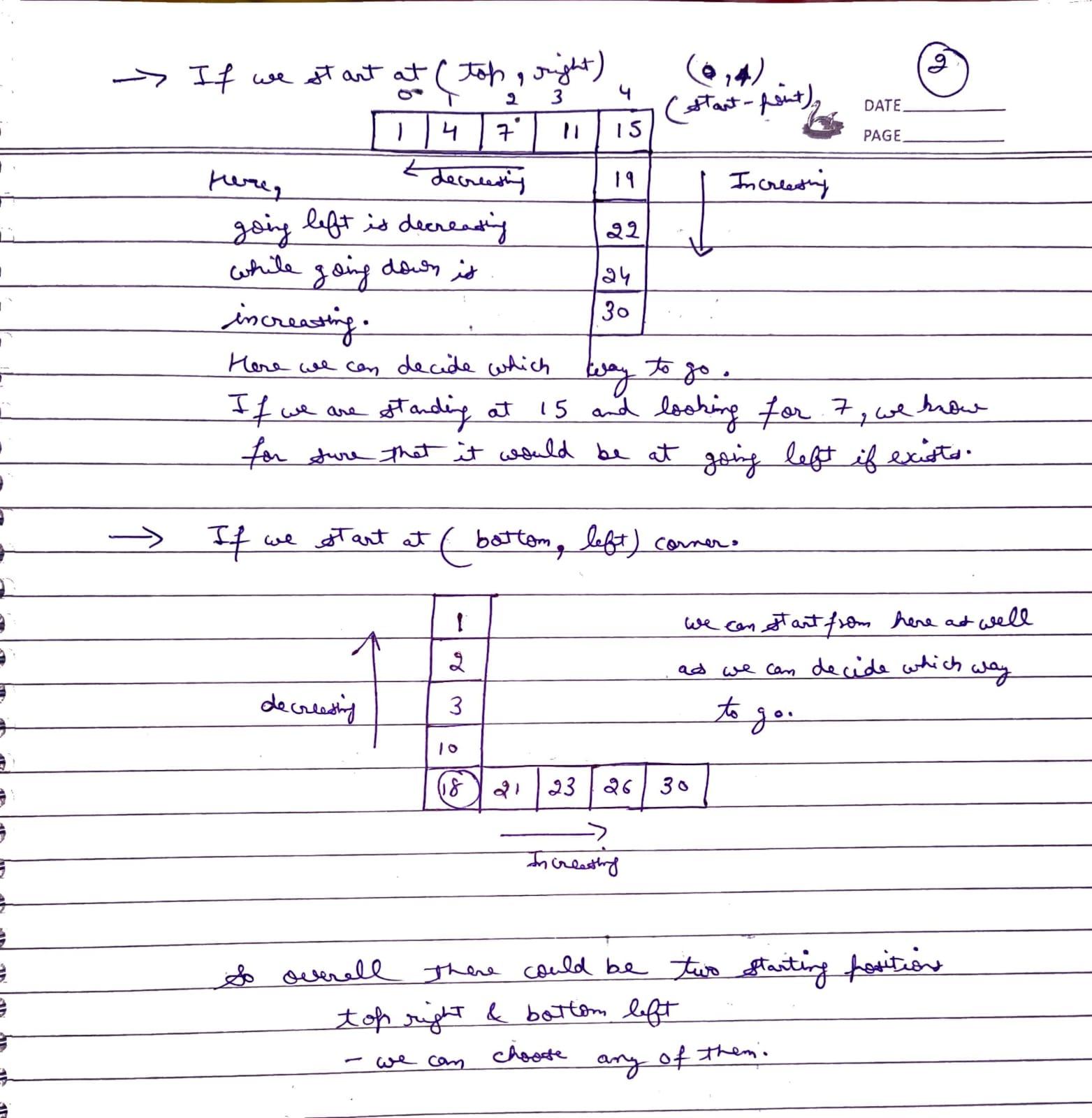
• Cell (0, m-1): Assume traversal starts from (0, m-1) and the search target is 14. In this case, the row is in decreasing order and the column is in increasing order. Therefore, if traversal begins from (0, m-1), the direction of movement can be easily determined based on these conditions.
  • If matrix[0][m-1] is greater than target: Move row-wise.
  • If matrix[0][m-1] is smaller than target: Bigger elements are needed, so move column-wise.
• Cell (n-1, m-1): Assume traversal starts from (n-1, m-1) and the search target is 14. Since both the row and column are sorted in decreasing order, it cannot be determined whether to proceed row-wise or column-wise. Therefore, traversal cannot be started from (n-1, m-1).
• Cell (n-1, 0): Assume traversal starts from (n-1, 0) and the search target is 14. In this case, the row is in increasing order and the column is in decreasing order. Therefore, if traversal begins from (n-1, 0), the direction of movement can be easily determined based on these conditions.
  • If matrix[n-1][0] is smaller than target: Move row-wise.
  • If matrix[n-1][0] is greater than target: Smaller elements are needed, move column-wise.
• From the above observations, it is quite clear that matrix traversal should be started from either the cell (0, m-1) or (n-1, 0).

Approach:

1. Let us take starting cell as (0, m-1), the two variables i.e. ‘row’ and ‘col’ will point to 0 and m-1 respectively.
2. Initialize a while loop, which will run till 'row' is less than n(total rows in the matrix) and 'col' is greater than or equal to 0.
3. If the element at the cell (row, col) is equal to target, return true as the target has been found.
4. If the element at the cell (row, col) is geater than target, it means smaller elements are needed to reach the target. But the column is in increasing order and so it contains only greater elements. So, eliminate the column by decreasing the current column value by 1(i.e. col--) and thus, move row-wise.
5. If the element at the cell (row, col) is smaller than target, it suggests that bigger elements are needed to reach the target. But the row is in decreasing order and so it contains only smaller elements. So, eliminate the row by increasing the current row value by 1(i.e. row++) and thus move column-wise.
6. If the loop terminates without getting any matching element, return false.

Code:

#include <bits/stdc++.h>
using namespace std;

class Solution {
public:
    //Function to search for a given target in matrix
    bool searchMatrix(vector<vector<int>>& matrix, int target) {
        int n = matrix.size();
        int m = matrix[0].size();
        
        //Intialize the row and col
        int row = 0, col = m - 1;

        //Traverse the matrix from (0, m-1):
        while (row < n && col >= 0) {
            
            //Return true of target is found
            if (matrix[row][col] == target) return true;
            else if (matrix[row][col] < target) row++;
            else col--;
        }
        //Return false if target not found
        return false;
    }
};

int main() {
    
    vector<vector<int>> matrix = {{1, 4, 7, 11, 15}, 
                                  {2, 5, 8, 12, 19},
                                  {3, 6, 9, 16, 22},
                                  {10, 13, 14, 17, 24},
                                  {18, 21, 23, 26, 30}};
    int target = 8;
    
    //Create an instace of Solution class
    Solution sol;
    
    bool result = sol.searchMatrix(matrix, target);
    
    // Output the result
    result ? cout << "true\n" : cout << "false\n";
    
    return 0;
}

Complexity Analysis:

• Time Complexity: O(N + M), where N is the number of rows in the matrix, M is the number of columns in each row. Traversal starts from (0, M-1), and at most, it can end up in the cell (M-1, 0). Therefore, the total distance can be at most (N+M). Hence, the time complexity is O(N+M).
• Space Complexity: As no additional space is used, so the Space Complexity is O(1).