Dynamic Programming

Dynamic Programming (DP) is a method (technique) for solving optimization problems by breaking them down into simpler, overlapping subproblems and solving each subproblem only once. It stores the solutions to these subproblems to avoid redundant computations, leading to a more efficient and optimized solution for the overall problem.

It can be think of as recursion with memory.

Recursion is essentially breaking down a big problem into smaller sub-problems so that it becomes so small that it becomes so small that you can finally solve it.

There is a well known quote that suits the dynamic programming:

Those who forget the past, are condemned to repeat it.

Dynamic programming is an algorithmic technique that breaks a problem down into smaller subproblems, computes solutions to these subproblems once, and then stores these solutions in a table for future use. This helps avoid redundant computations and saves time.

Real Life Example

Imagine you are trying to climb a tall mountain, and you can only take small steps. You want to reach the top as quickly as possible.

Now, instead of looking at the entire mountain and getting overwhelmed, you break down the task. You say, "If I want to reach the top, I must first reach a point, let's call it point A. From point A, I need to reach point B, and so on until I reach the top."

Dynamic programming is like making a map of the mountain with all the little steps marked. Once you've figured out the best way to get from one step to the next, you write it down. So, the next time you come across that step, you don't need to figure it out again. You already know the best way to get from there to the top.

Why Dynamic Programming is used?

Let's consider a classic example the computation of Fibonacci numbers:

The Fibonacci sequence is a sequence of numbers, where each number is calculated by adding the previous two together.

F(n)=F(n−1)+F(n−2)

with base cases:

F(0)=0,F(1)=1

Below is the fibonacci code with recursion:

#include <iostream>

long long fibonacci(int n) {
    if (n <= 1) {// if n ==0 or n ==1
        return n;
    }

    return fibonacci(n - 1) + fibonacci(n - 2);
}

int main() {
    int n = 5;
    std::cout << "Fibonacci(" << n << ") = " << fibonacci(n) << std::endl;

    return 0;
}

A naive recursive implementation of Fibonacci can be quite inefficient because it involves redundant computations. For example, if you were to calculate F(6), the recursive calls would look like this:

F(6) = F(5) + F(4) = (F(4) + F(3)) + (F(3) + F(2))

Notice that F(3) and F(2) are calculated multiple times, leading to inefficiency as the sequence grows.

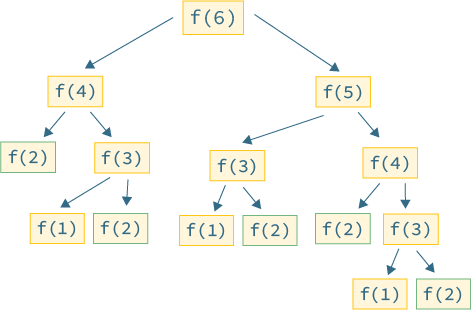
This is where dynamic programming comes in. By using memoization or tabulation, we can store the results of previously calculated Fibonacci numbers and reuse them when needed, avoiding redundant computations.

The Time complexity of the naive recursive Fibonacci algorithm is exponential, specifically O(2^n), where n is the input number representing the position in the Fibonacci sequence.

Let's analyze the time complexity:

1. Recurrence Relation:
   The recurrence relation for the naive recursive Fibonacci algorithm is given by:
   T(n) = T(n-1) + T(n-2) + O(1)
   where 

Here's a simple example in C++ using memoization:

#include <iostream>
#include <unordered_map>

std::unordered_map<int, long long> memo;

long long fibonacci(int n) {
    if (n <= 1) {
        return n;
    }

    // Check if result for 'n' is already memoized
    if (memo.find(n) != memo.end()) {
        return memo[n];
    }

    // Calculate Fibonacci recursively and memoize the result
    memo[n] = fibonacci(n - 1) + fibonacci(n - 2);

    return memo[n];
}

int main() {
    int n = 5;
    std::cout << "Fibonacci(" << n << ") = " << fibonacci(n) << std::endl;

    return 0;
}

Fibonacci Sequence

1 Brute Force Recursion

The mathematics form of Fibonacci sequence is recursive, which in code is like this:

int fib(int N) {
    if (N == 1 || N == 2) return 1;
    return fib(N - 1) + fib(N - 2);
}

We don't need to say too much about this, teachers at school all seem to use this as an example of recursion. We also know writing codes this way is easy but inefficient. Where is inefficient? Suppose n is 20 and draw the recursive tree.

PS: Every time you meet the problems needed to be recursive, you'd better draw the recursive tree, which is of great help for you to find the reason of inefficiency.

How to understand this recursive tree? That is to say to calculate the ordinary problem f(20), we need to calculate f(19) and f(18), then f(19), we need to calculate f(18) and f(17) first, and so on.

How to calculate the time complexity? It is number of subproblems multiplied by the time to solve a subproblem.

The number of subproblems, namely the total number of nodes in recursive tree. Obviously the number of nodes in binary tree is exponential, so the number of subproblems is O(2^n), as the time to solve a subproblem here is without cycles, only with the add operation f(n-1) + f(n-2) of which the time is O(1), so the time to solve a subproblem is O(2^n), which is exponential, bang.

Observe the recursive tree, we can find the reason why the algorithm is inefficient: there exist a lot of repeated calculation, for example, f(18) is calculated twice, and as you can see, the recursive tree rooted at f(19) has a so huge volume that every one turn of calculation wastes a lot of time, moreover, more than the node f(18) is calculated repeatedly, so this algorithm is very inefficient.

This is the first property in DP: overlapped subproblem.

2 Recursive Solution with memos

To know well the problem is to solve a half. Since the reason for wasting time is repeating calculation, then we can make a memo, every time you obtain the answer of a subproblem , record it to the memo and then return; every time you meet a problem of memo check the memo, if you find you have solved that before, just take the answer out for use, and do not waste time to calculate.

Generally an array is used as a memo, of course you can use hash table (dictionary), the thought is the same.

int fib(int N) {
    if (N < 1) return 0;
    // memo initialized as 0
    vector<int> memo(N + 1, 0);
    // initialize the easiest condition
    return helper(memo, N);
}

int helper(vector<int>& memo, int n) {
    // base case 
    if (n == 1 || n == 2) return 1;
    // having calculated
    if (memo[n] != 0) return memo[n];
    memo[n] = helper(memo, n - 1) + 
                helper(memo, n - 2);
    return memo[n];
}

Now, draw the recursive tree, and you will know what memo does.

How to calculate the time complexity? The number of subproblems multiplied by the time of which the subproblem needs.

The number of total subproblems, namely the total number of nodes in graph, because there is no redundant computation in this algorithm, the subproblems are f(1),f(2),f(3)...

f(20), the number and size of input n = 20 are directly proportional, so the number of subproblems are O(n).

The time to solve a subproblem, as above, there is no loop, the time is O(1).

Therefore, the time complexity of this algorithm is O(n). Instead of a brute-force algorithm, it's a dimension reduction attack.

So far, the efficiency of the recursive solution with memos is the same as that of the iterative dynamic programming solution. In fact, this approach is almost identical to iterative dynamic programming, except that it is called "top-down" and dynamic programming is called "bottom-up".

What is "top down"? Notice that the recursion tree that we just drew, or the graph, goes from the top down, all the way down from a big old problem like f(20), and gradually breaks down the size until f(1) and f(2) hit the bottom, and then returns the answer layer by layer, which is called top-down.

What is "bottom-up"? In turn, we start directly from the bottom, the simplest, smallest problem, f(1) and f(2), and we push it up, until we get to the answer we want, f(20), and that's the idea of dynamic programming, and that's why dynamic programming is generally done without recursion, by iteration.

3 Recursive answer to dp array

Have the inspiration of last step "memorandum", we can separate this "memorandum" into a table, called DP table, in this table to complete the "bottom up" calculation is not beautiful!

int fib(int N) {
    vector<int> dp(N + 1, 0);
    // base case
    dp[1] = dp[2] = 1;
    for (int i = 3; i <= N; i++)
        dp[i] = dp[i - 1] + dp[i - 2];
    return dp[N];
}

It makes sense to draw a picture, and you see that the DP table looks very much like the result of the "pruning" before, only in reverse.In fact, the "memo" in the recursive solution with memo is the DP table after the final completion, so the two solutions are actually the same, in most cases, the efficiency is basically the same.

Here, we introduce the term "state transition equation", which is actually the mathematical form to describe the structure of the problem:

Why is it called the "state-transition equation"? To sound fancy. You want f of n to be a state n, and that state n is transferred from the sum of the states n minus 1 and n minus 2, that's called a state transfer – that's all.

You will find that all the operations in the above solutions, such as return f(n - 1) + f(n - 2), dp[i] = dp[i - 1] + dp[i - 2], and the initialization of the memo or dp table, all revolve around different representations of this equation. It is important to list the "state transfer equation", which is the core of the solution. It's easy to see that the equation of state transition directly represents the brute-force solution.

Categories of Dynamic Programming

Dynamic programming can be categorized into two main types: top-down with memoization (recursive) and bottom-up with tabulation (iteration)

Top-Down with Memoization (Recursive):

In this approach, the problem is solved in a recursive manner, breaking it down into smaller subproblems. However, to avoid redundant computations, the solutions to subproblems are memoized, meaning they are stored in a data structure (like a hash table, or an array) for quick retrieval. If a subproblem has already been solved, its solution is retrieved from the memoization table rather than recalculating it. This method is often more intuitive and easier to implement.

#include <iostream>
#include <unordered_map>

std::unordered_map<int, long long> memo;

long long fibonacci(int n) {
    if (n <= 1) {
        return n;
    }

    if (memo.find(n) != memo.end()) {
        return memo[n];
    }

    memo[n] = fibonacci(n - 1) + fibonacci(n - 2);

    return memo[n];
}

int main() {
    int n = 5;
    std::cout << "Fibonacci(" << n << ") = " << fibonacci(n) << std::endl;

    return 0;
}

Bottom-Up with Tabulation (Iterative):

In this approach, the problem is solved by iteratively filling up a table or an array with the solutions to subproblems in a bottom-up manner. The algorithm starts by solving the smallest subproblems and gradually builds up to the desired solution. This method often uses less space compared to memoization since it doesn't need to store solutions for all possible subproblems in advance.

#include <iostream>
#include <vector>

long long fibonacci(int n) {
    if (n <= 1) {
        return n;
    }

    std::vector<long long> dp(n + 1, 0);
    dp[1] = 1;

    for (int i = 2; i <= n; ++i) {
        dp[i] = dp[i - 1] + dp[i - 2];
    }

    return dp[n];
}

int main() {
    int n = 5;
    std::cout << "Fibonacci(" << n << ") = " << fibonacci(n) << std::endl;

    return 0;
}