Introduction

In the most basic computer science sense, recursion is a function that calls itself. Recursion is a method of solving problems based on the divide and conquer mentality. The basic idea is that you take the original problem and divide it into smaller (more easily solved) instances of itself, solve those smaller instances (usually by using the same algorithm again) and then reassemble them into the final solution.

Simple English example of recursion:

A child couldn't sleep, so her mother told her a story about a little frog,
    	who couldn't sleep, so the frog's mother told her a story about a little bear,
         	who couldn't sleep, so the bear's mother told her a story about a little weasel... 
            	who fell asleep.
         	...and the little bear fell asleep;
    	...and the little frog fell asleep;
...and the child fell asleep.

What is Recursion?

• Recursion is a programming technique where a function calls itself directly of indirectly to solve a problem.
• It involves breaking down a problem into smaller subproblems of the same type.

Basic Principles of recursion:

• Base case: Every recursive algorithm must have a base case, which is the condition that terminates the recursion. It represents the simplest form of the problem and does not involve any further recursive calls.
• Recursive Case: This is the case where the function calls itself with a smaller instance of the problem. It makes progress towards the base case..

Recursive Function

A recursive function is a function that calls itself either directly or indirectly.

 return_type function_name(parameters) {
    // Base case
    if (base_case_condition) {
        // Base case: return some value
    }
    // Recursive case
    else {
        // Call the function recursively with smaller input
        return function_name(smaller_input);
    }
}

As an example, consider the factorial of a nonnegative integer:

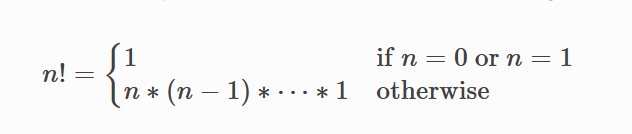
We can implement an iterative function to compute this:

// REQUIRES: n >= 0
// EFFECTS: Computes and returns n!.
int factorial(int n) {
  int result = 1;
  while (n > 0) {
    result *= n;
    --n;
  }
  return result;
}

On the other hand, we can observe that (n-1)! = (n-1)* . .* 1, so that we can mathematically define factorial in terms of itself:

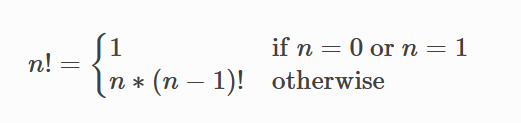
Such a mathematical definition is called a recurrence relation. It translated into code as follows:

// REQUIRES: n >= 0
// EFFECTS: Computes and returns n!.
int factorial(int n) {
  if (n == 0 || n == 1) {
    return 1;
  } else {
    return n * factorial(n - 1);
  }
}

This function is recursive, since it calls itself as part of its definition. We can then call factorial() as follows:

int main() {
  int result = factorial(3);
  cout << "3! = " << result << endl;
}

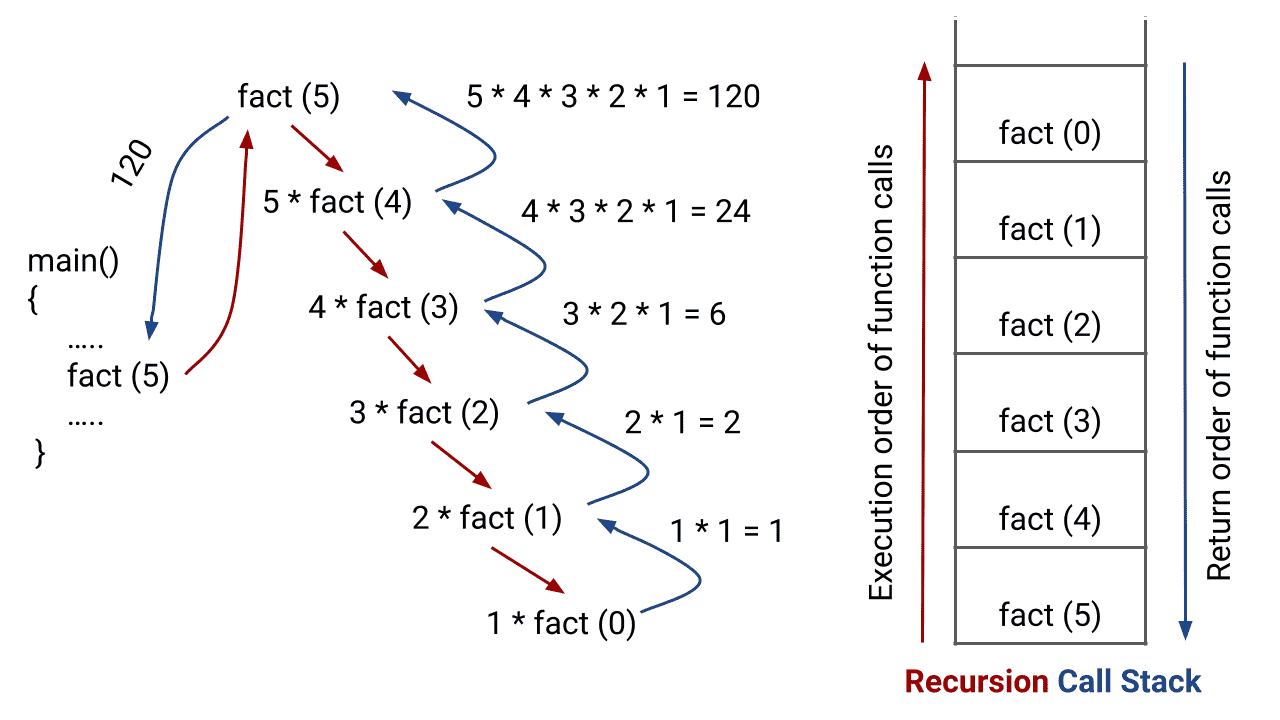
This activation records created by this program as show below:

When the call factorial(3) is evaluated, an activation record is created, and the parameter n is initialized with value 3. The body of factorial() runs, and it calls factorial(2). This creates another activation record, and its parameter n is initialized to 2. Within the context of that activation record, the body of factorial() is executed, and it calls factorial(1). Another activation record is created, with n initialized to 1. The body runs, returning 1, which replaces the function call in the caller. The activation record for factorial(1) is destroyed, and factorial(2) resumes. The latter computes 2 * 1 and returns 2. The activation record for factorial(2) is destroyed, and factorial(3) continues where it left off. It computes 3 * 2, returning 6. Its activation record is reclaimed, and main() resumes, initializing result to 6, the correct value for 3!.

Iteration vs Recursion

Iteration and recursion are two alternative approaches to solving problems in programming.

Iteration:

Iteration is a programming technique that involves repeating a set of instructions a specified number of times or until a particular condition is met. It involves using loops like for, while, or do-while.

1. Iteration involves using loops (like for loop, while loop) to repeatedly execute a set of instructions until a certain condition is met.
2. It uses less memory as compared to recursion.
3. It is generally faster and more efficient than recursion.
4. It is often easier to understand for beginners.

Recursion:

Recursion is a programming technique where a function calls itself in its definition. Each recursive call solves a part of the problem, and the solutions are combined to solve the complete problem.

1. Recursion involves a function calling itself, either directly or indirectly.
2. It generally uses more memory as compared to iteration because each function call adds a new layer to the call stack.
3. Recursion can be slower and less memory-efficient than iteration due to the overhead of function calls.
4. It can be more elegant and intuitive for certain problems, especially those that can be naturally divided into smaller, similar subproblems.

Comparison:

1. Termination Condition:
   1. Iteration: It uses loop constructs like for, while, or do-while where termination conditions are explicitly defined.
   2. Recursion: It relies on a base case to terminate the recursive calls.
2. Memory Usage:
   1. Iteration: Generally, iteration uses less memory as compared to recursion.
   2. Recursion: Each recursive call consumes memory as it adds a new stack frame to the call stack.
3. Readability:
   1. Iteration: Sometimes iteration may lead to more readable and understandable code.
   2. Recursion: Recursion can sometimes make the code more elegant and easier to understand, especially for problems that can be naturally divided into smaller similar sub-problems.
4. Performance:
   1. Iteration: Iterative solutions are often more efficient in terms of performance and memory usage for problems that can be solved iteratively.
   2. Recursion: Recursive solutions can be less efficient due to the overhead of function calls and maintaining the call stack. However, for some problems, recursion can be the most elegant and efficient solution.
      The actual time taken can be much higher than the iterative approach due to overhead of function calls and maintaining the call stack.
5. Time Complexity:
   1. Iteration: For the problem of factorial it has time time complexity of O(n).
   2. Recursion: It has actual time complexity of O(2*n), but we just ignore the constant and write it as O(n).

When to use Recursion vs Iteration?

In general, recursion should be used when it produces a cleaner, more expressive solution compared to the iterative version, and when you know that an excessive number of recursive calls will either not occur, or not lead to performance issues such as stack overflow.

Keep in mind that "recursion" and "loops" are just what we humans name our code -- what matters for performance is not how we name things, but rather how they are compiled or interpreted. Thus performance depends on the specific programming language and code being used.

In most imperative programming languages (eg. C, Python, Ruby), recursion is generally more expensive than iteration because it requires winding, or pushing new stack frames1 onto the call stack2 each time a recursive function is invoked -- these operations take up time and stack space, which can lead to an error called stack overflow if the stack frames consume all of the memory allocated for the call stack.

Thus the main drawback with recursion is that it has linear, or O(n), stack space requirements while for an iterative function it is constant, or O(1).