Neural Networks Theory

Neural networks are computational models inspired by the structure and function of the human brain. They consist of interconnected processing units—commonly called neurons—that work together to solve complex problems. Below is an in‐depth explanation of neural networks, covering their architecture, training processes, and key components.

Fundamental Architecture

Neurons:

A neuron is a basic processing unit that received input signals, applies a transformation (often a weighted sum), and passes the result through an activation function. Mathematically, a neuron computes:

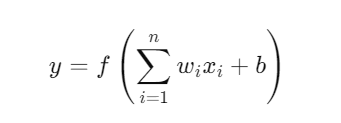
where:

• xi are the inputs,
• wi are the corresponding weights,
• b is the bias, 
• f is the activation function,
• y is the output of the neuron.

Inputs:

A neuron receives one or more input signals. These inputs can come directly from data or from the outputs of neurons in a previous layer.

Weights:

Each input is associated with a weight, which represents the strength or importance of that input. The neuron computes a weighted sum of its inputs. During the training process weights are modified.

Bias:

In addition to the weighted inputs, a bias term is added. This term allows the activation function to be shifted, giving the neuron greater flexibility in its output. The bias is added to the weighted sum of inputs before applying the activation function. It's role is to provide every neuron with a trainable constant value, enabling the model to shift the activation function horizontally. This means that even if all input features are zero, the neuron can still produce a non-zero output.

Activation Function:

The weighted sum plus bias is passed through an activation function (such as sigmoid, ReLU, or tanh). This non-linear function determines the neuron's output by introducing non-linearity, which enables the network to learn complex patterns.

Layers:

Neural networks are organized in layers:

• Input Layer: Receives the raw data.
• Hidden Layer: Intermediate layers where computation are performed. Deep networks may have many hidden layers, allowing them to learn hierarchical representations.
• Output Layer: Produces the final output, such as a class label in classification tasks or a continuous value in regression tasks.

Network Topology

• Feedforward Networks:
  Data flows in one direction—from input to output—without cycles.
• Recurrent Networks:
  They include loops allowing information to persist, which is useful for sequential data like time series or language.
• Convolutional Networks:
  Specially designed for grid-like data such as images; they employ convolutional layers to capture spatial hierarchies.

Activation Functions

Activation functions introduce non-linearity into the model, enabling the network to learn complex patterns. Common choices include:

Sigmoid:

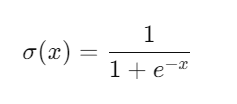
• Useful for binary classification but can suffer from vanishing gradients.

ReLU (Rectified Linear Unit):

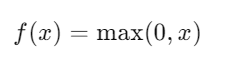
• Popular due to its simplicity and efficiency in mitigating the vanishing gradient problem.

Tanh:

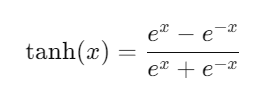
• Scales input to the range [-1, 1].