Undirected graph
An undirected graph is a graph in which the edges do not point in any direction (i.e., the edges are bidirectional).
(A)-----(C)
| |
| |
| |
(D)-----(B)Connected Graph
A connected graph is a graph in which there is always a path from a vertex to any other vertex.
(A) (B)
\ |
\ |
\ |
\ |
(D)-----(C)Spanning Tree
A spanning tree is a sub-graph of an undirected connected graph, which includes all the vertices of the graph with a minimum possible number of edges. If a vertex is missed, then it is not a spanning tree.
A spanning tree is a subset of Graph G, such that all the vertices are connected using minimum possible number of edges. Hence, a spanning tree does not have cycles and a graph may have more than one spanning tree.
Given a connected, undirected graph G with n vertices and m edges, a spanning tree is a subgraph of G that:
- Includes all the vertices of the graph.
- Forms a tree (i.e., it is connected and acyclic).
It has number of edges = number of vertices - 1
A Spanning tree does not have any cycle.
Number of Spanning trees in a complete graph with n vertices is
n^ n-2, This formula is for complete graph in which every vertices connected to very other vertices.

This is a complete graph (in which every node is connected to every other node):
Here n = 4
So number of possible spanning tree are = n^ n-2 = 4^ (4-2) = 4^2 = 16 (As shown in the image above).
Example:
Let the original graph be:
(A)-----(C)
| |
| |
| |
(D)-----(B)Some of the possible spanning trees that can be created from the above graph are:
(A)-----(C)
|
|
|
(D)-----(B) (A)-----(C)
|
|
|
(D)-----(B) (A) (C)
| |
| |
| |
(D)-----(B) (A)-----(C)
| |
| |
| |
(D) (B) (A)-----(C)
| \
| \
| \
(D) (B) (A) (C)
| / |
| / |
| / |
(D) (B)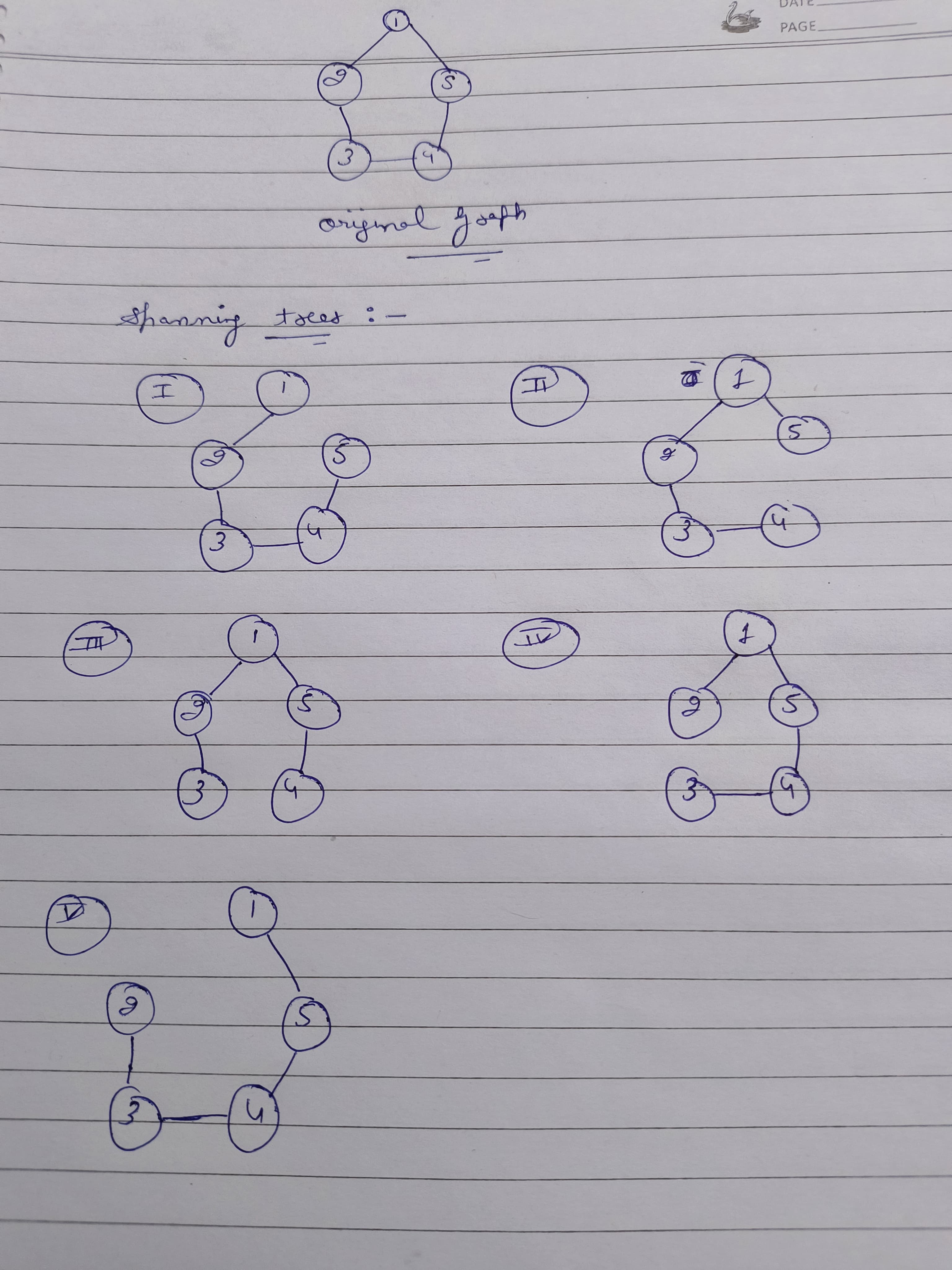
Minimum Spanning Tree
A minimum spanning tree is a spanning tree in which the sum of the weight of the edges is as minimum as possible.
Given a connected, undirected graph G with n vertices and m edges, a Minimum Spanning Tree is a tree that:
- Includes all the vertices of the graph.
- Forms a subgraph that is a tree (i.e., it is connected and acyclic).
- Has the minimum possible sum of edge weights among all such trees.
An MST with V vertices (where V is the number of vertices in the original graph) will have exactly V – 1 edges, where V is the number of vertices.
An MST is optimal for minimizing the total edge weight, but it may not necessarily be unique.
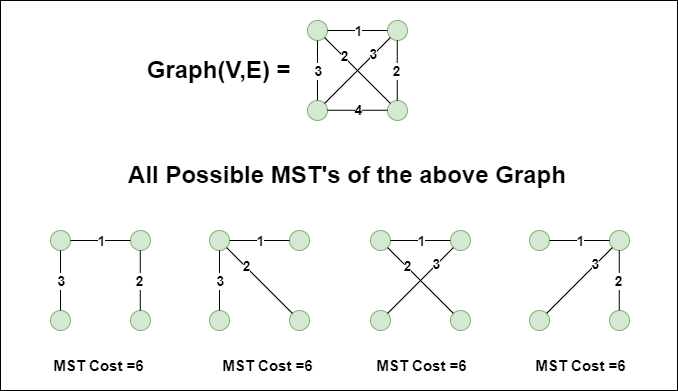
Example of a Spanning Tree:
Let's understand the above definition with the help of example below.
The initial graph is:
(A)--1--(C)
| |
2 4
| |
(D)--3--(B)
Weighted graphThe possible spanning trees from the above graph are:
(A)--1--(C)
|
2
|
(D)--3--(B)
Sum = 1 + 2 + 3 = 6 (A)--1--(C)
|
4
|
(D)--3--(B)
Sum = 1 + 4 + 3 = 8 (A) (C)
| |
2 4
| |
(D)--3--(B)
Sum = 2 + 3 + 4 = 9 (A)--1--(C)
| |
2 4
| |
(D) (B)
Sum = 1 + 2 + 4 = 7The minimum spanning tree from the above spanning trees is:
(A)--1--(C)
|
2
|
(D)--3--(B)
Sum = 1 + 2 + 3 = 6The minimum spanning tree from a graph is found using the following algorithms:
- Kruskal's Algorithm
- Prim's Algorithm
Algorithms to Find Minimum Spanning Tree
1 Kruskal's Algorithm:
Kruskal's algorithms is a greedy algorithm used to find the Minimum Spanning Tree (MST) of a connected, undirected graph. The MST is a subset of the edges of the original graph that connects all the vertices together with the minimum possible total edge weight.
- This algorithm employs a greedy approach, meaning it makes locally optimal choices at each step to achieve a globally optimal solution.
Understanding
The main idea behind Kruskal's algorithm is to sort all the edges of the graph in non-decreasing order of their weights and then add them to the MST one by one, starting from the smallest weight edge, as long as adding the edge does not form a cycle in the MST.
Algorithm:
- Sort all the edges of the graph in non-decreasing order of their weights.
- Initialize an empty graph T to store the MST.
- Iterate through all the edges in the sorted order.
- For each edge (
u,v,w), whereuandvare vertices andwis the weight of the edge:- If adding the edge (
u,v) to the MSTTdoes not form a cycle, add the edge toT. - Otherwise, skip the edge.
- If adding the edge (
- Continue this process until all vertices are connected.
Example:
A -----6------B
/ | / | \
7 | / | 5
/ | / | \
C 3 4 2 F
\ | / | /
8 | / | 2
\ | / | /
D------3------E
Graph GThis graph can have multiple spanning tree:
The main idea of Kruskal's algorithm to find the MST of a graph G with V vertices and E edges is
- To sort all the edges in ascending order according to their weights.
- Then select the first
V-1edges such that they do not form any cycle within them.
- We will write all the edges sorted in ascending order according to their respective weights.
- Then we will select the first
V-1 = 5edges which do not form cycles.
- Step 1 - Sort the edges in ascending order. Here is the list after sorting.
| No. | u | v | Weight |
| 1 | B | E | 2 |
| 2 | E | F | 2 |
| 3 | D | E | 3 |
| 4 | A | D | 3 |
| 5 | B | D | 4 |
| 6 | B | F | 5 |
| 7 | A | B | 6 |
| 8 | A | C | 7 |
| 9 | C | 8 | 8 |
- Step 2 - Choose 5 edges from starting which do not form a cycle.
Pick edge B<=>E, This is the first edge so it can't form any cycle hence including this in result.
B
|
|
|
2
|
|
|
EPick edge, E<=>F, and D<=>E as they have the next non-decreasing weights, and they do not form any cycle.
B
|
|
|
2 F
| /
| 2
| /
D------3------EPick edge, A<=>D, as they have the next non-decreasing order and does not form the loop.
A B
| |
| |
| |
3 2 F
| | /
| | 2
| | /
D------3------EThe next non-decreasing edges are, D<=>B having edge (4), B<=>F having edge(5) and A<=>B having edge(6) but all of these cause cycle.
Go on next non-decreasing edge, which is A<=>C having edge (7).
A B
/ | |
7 | |
/ | |
C 3 2 F
| | /
| | 2
| | /
D------3------EAfter covering all nodes, and n-1 edges the above is our MST.
Calculated weight of the MST = 7 + 3 + 3 + 2 + 2 = 17
Code Implementation:
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
// Structure to represent an edge
struct Edge {
int u, v, weight;
};
// Comparator function to sort edges by weight
bool compare(Edge a, Edge b) {
return a.weight < b.weight;
}
// Find function to find the parent of a vertex
int findParent(int u, vector<int>& parent) {
if (parent[u] == u)
return u;
// Path compression
return parent[u] = findParent(parent[u], parent);
}
// Union function to union two sets
void unionSet(int u, int v, vector<int>& parent, vector<int>& rank) {
int pu = findParent(u, parent);
int pv = findParent(v, parent);
// Union by rank
if (rank[pu] < rank[pv])
parent[pu] = pv;
else if (rank[pu] > rank[pv])
parent[pv] = pu;
else {
parent[pu] = pv;
rank[pv]++;
}
}
// Kruskal's algorithm to find Minimum Spanning Tree
vector<Edge> kruskalMST(vector<Edge>& edges, int n) {
vector<Edge> result;
vector<int> parent(n);
vector<int> rank(n, 0);
// Initialize parent array and rank array
for (int i = 0; i < n; ++i)
parent[i] = i;
// Sort edges by weight
sort(edges.begin(), edges.end(), compare);
// Iterate through all edges
for (Edge edge : edges) {
int u = edge.u;
int v = edge.v;
int weight = edge.weight;
// If adding the edge (u, v) does not form a cycle
if (findParent(u, parent) != findParent(v, parent)) {
result.push_back(edge); // Add edge to MST
unionSet(u, v, parent, rank); // Union the sets
}
}
return result;
}
int main() {
int n = 4; // Number of vertices
// Example graph with edges and weights
vector<Edge> edges = {
{0, 1, 2},
{0, 3, 2},
{1, 2, 1},
{1, 3, 3},
{2, 3, 5}
};
// below is the structure of it
0-----------2------------1
| / |
| / |
| / |
| / |
| / |
2 3 1
| / |
| / |
| / |
| / |
3-----------5------------2
// Find Minimum Spanning Tree
vector<Edge> mst = kruskalMST(edges, n);
// Print Minimum Spanning Tree
cout << "Minimum Spanning Tree:" << endl;
for (Edge edge : mst)
cout << edge.u << " - " << edge.v << " : " << edge.weight << endl;
return 0;
}
Complexity Analysis:
Time Complexity:
- Sorting the edges:
O(E log E) - Finding parent and union operations:
O(E log ∗ V)with path compression and union by rank. - Overall time complexity:
O(E log E+E log ∗ V) - In most cases,
E≪V^2, soO(E log E)dominates. - Hence, the time complexity is approximately
O(E log E).
Space Complexity:
- The space complexity is
O(V+E)for storing the graph and the MST.
2 Prim's Algorithm
Prim's algorithm is a greedy algorithm used to find the Minimum Spanning Tree (MST) of a connected, undirected graph. The algorithm starts with an arbitrary vertex as the initial tree and grows the tree by adding the cheapest edge that connects the tree to a vertex not yet in the tree. Prim's algorithm is efficient and guarantees to find the minimum spanning tree of the graph.
Leave a comment
Your email address will not be published. Required fields are marked *