In this chapter we will parse the print keyword in FarmScript.

#1 Input Program String

print "Hi";

Above written snippet will be our program. Which should print “Hi” in the terminal console.

#2 Lexical Analysis (Tokenization):

You know very well now, That the very first phase of the interpretation is the tokenization in which we scan the characters and group them in the corresponding token.

	Scanner scanner(source);
    std::vector<Token> tokens = scanner.scanTokens();

Below will be the output of the lexical analysis:

Token.lexeme = print
Token.line = 1
Token.type = 33
TokenTypeName = PRINT

Token.lexeme = "Hi"
Token.line = 1
Token.type = 22
TokenTypeName = STRING

Token.lexeme = ;
Token.line = 1
Token.type = 8
TokenTypeName = SEMICOLON

Token.lexeme =
Token.line = 2
Token.type = 41
TokenTypeName = EOF_TOKEN

#3 Parse Print statement

	Parser parser(tokens);
    std::vector<Stmt *> statements = parser.parse();

std::vector<Stmt *> Parser::parse()
{
    std::vector<Stmt *> result;
    while (!isAtEnd())
    {
        Stmt *stmt  = declaration();
        if (FarmScript::hadError)
        {
            synchronize();
            if (stmt)
            {
                delete stmt;
            }
            stmt = nullptr;
            break;
        }
        else
        {
            result.push_back(stmt);
        }
    }
    return result;
}

Stmt * Parser::declaration()
{
    if (match(FUN))
    {
        return (Stmt *)function("function");
    }
    else if (match(CLASS))
    {
        return classDeclaration();
    }
    else if (match(VAR))
    {
        return varDeclaration();
    }
    return statement();
}

Stmt * Parser::statement()
{
    if (match(PRINT))
    {
        return printStatement();
    }
    else if (match(LEFT_BRACE))
    {
        return blockStatement();
    }
    else if (match(IF))
    {
        return ifStatement();
    }
    else if (match(WHILE))
    {
        return whileStatement();
    }
    else if (match(FOR))
    {
        return forStatement();
    }
    else if (match(BREAK))
    {
        return breakStatement();
    }
    else if (match(RETURN))
    {
        return returnStatement();
    }
    return expressionStatement();
}

• If the current token matches the PRINT token, it calls the printStatement() method to parse the print statement.

#3.1 printStatement()

Stmt * Parser::printStatement() {
    Expr *expr = expression(); // Parse the expression to be printed
    // Check for semicolon to terminate the print statement
    if (consume(SEMICOLON, "Expected ';' after value.")) {
        return new Print(expr); // Return Print statement with parsed expression
    } else {
        delete expr; // Clean up the expression if semicolon is missing
        return nullptr; // Return null pointer if semicolon is missing
    }
}

– Parse Expression:

• It calls the expression() method to parse the expression to be printed.

– Consume Semicolon:

• It checks for a semicolon ; to terminate the print statement.
• If the semicolon is found, indicating the end of the print statement, it creates a Print statement object with the parsed expression and returns it.

struct Print : public Stmt
{
    Expr *expression;

    Print(Expr *expression) : Stmt(StmtType_Print), expression(expression) {}

    ~Print();
};

– Error Handling:

• If the semicolon is missing after the expression, it generates an error message using the consume method and returns a null pointer.
• Before returning a null pointer, it also cleans up the memory allocated for the parsed expression.

#3.1.1 expression()

Expr * Parser::expression() {
    Expr *expr = assignment(); // Parse an assignment expression
    return expr; // Return the parsed expression
}

– Parse Assignment Expression:

• The assignment() method is responsible for parsing assignment expressions, which typically involve variable assignment or compound assignments +=, -=, etc.
• This method likely handles parsing expressions with the lowest precedence level.

– Return Parsed Expression:

• After parsing the assignment expression, the method returns the resulting Expr object.
• This returned expression may represent a single assignment or a more complex expression involving multiple assignments and operators.

assignment()

Expr * Parser::assignment() {
    Expr *expr = conditional(); // Parse a conditional expression

    if (match(EQUAL)) {
        Token equals = previous(); // Get the token for the assignment operator

        // Check if the expression on the left-hand side of the assignment is a variable or a property access
        if (expr->type == ExprType_Variable) {
            Expr *value = assignment(); // Parse the right-hand side of the assignment
            Variable *variable = (Variable *)expr; // Cast the expression to a Variable
            Token *name = new Token(*variable->name); // Create a copy of the variable name token
            delete expr; // Delete the original expression
            return new Assign(name, value); // Return an Assign expression representing the assignment
        } else if (expr->type == ExprType_Get) {
            Get *get = (Get *)expr; // Cast the expression to a Get
            Expr *value = assignment(); // Parse the right-hand side of the assignment
            return new Set(get->object, get->name, value); // Return a Set expression representing property assignment
        }

        error(equals, "Invalid assign target."); // Report an error if the target of the assignment is invalid
    }

    return expr; // Return the parsed expression
}

– Parse Conditional Expression:

• The method starts by calling the conditional() method to parse a conditional expression.
• The conditional() method is likely responsible for parsing expressions involving ternary conditional operators (? :) or logical OR (||) operations.

– Check for Assignment Operator:

• If the next token is an equal sign (=) indicating an assignment, it continues parsing the assignment expression.
• It also retrieves the token for the equal sign using the previous() method.

– Handle Assignment to Variable or Property:

• It checks if the expression on the left-hand side of the assignment is either a variable or a property access.
• If it's a variable, it parses the right-hand side of the assignment and creates an Assign expression.
• If it's a property access, it parses the right-hand side of the assignment and creates a Set expression.

Expr * Parser::conditional() {
    Expr *expr = logic_or(); // Parse a logical OR expression

    if (match(QUESTION)) { // Check if the next token is a question mark (?)
        Token *question = new Token(previous()); // Get the token for the question mark
        Expr *second = conditional(); // Parse the second expression
        if (match(COLON)) { // Check if the next token is a colon (:)
            Token *colon = new Token(previous()); // Get the token for the colon
            Expr *third = conditional(); // Parse the third expression
            // Create a Ternary expression representing the conditional operator
            expr = new Ternary(expr, question, second, colon, third);
        } else {
            error(peek(), "Expected ':'"); // Report an error if ':' is missing
            delete question; // Clean up allocated memory for the question token
            delete second; // Clean up allocated memory for the second expression
        }
    }

    return expr; // Return the parsed expression
}

– Parse Conditional Expression:

• The method starts by calling the logic_or() method to parse a logical OR expression.
• The logic_or() method likely handles parsing logical OR operations (||) and expressions with higher precedence.

– Handle Ternary Conditional Operator:

• If the next token is a question mark (?), it proceeds to parse the second expression (for the true condition).
• After parsing the second expression, it expects a colon (:) token to separate the true and false conditions.
• If the colon token is found, it parses the third expression (for the false condition) and creates a Ternary expression representing the ternary conditional operator (expr ? second : third).
• If the colon token is missing, it reports an error indicating that a colon was expected.

Expr * Parser::logic_or() {
    Expr *expr = logic_and(); // Parse a logical AND expression

    // Loop to handle multiple OR operators
    while (match(OR)) { // Check if the next token is an OR operator
        Token *oper = new Token(previous()); // Get the token for the OR operator
        Expr *right = logic_and(); // Parse the right-hand side expression
        // Create a Logical expression node representing the OR operation
        expr = new Logical(expr, oper, right);
    }

    return expr; // Return the parsed expression
}

– Parse Logical AND Expression:

• The method starts by calling the logic_and() method to parse a logical AND expression.
• The logic_and() method likely handles parsing logical AND operations (&&) and expressions with higher precedence.

– Handle Multiple OR Operators:

• While there are consecutive OR operators (||) in the source code, the method continues to parse logical AND expressions on the right-hand side of each OR operator.
• For each OR operator encountered, it creates a Logical expression node representing the OR operation between the previously parsed expression (expr) and the newly parsed right-hand side expression.

Expr * Parser::logic_and() {
    Expr *expr = equality(); // Parse an equality expression

    // Loop to handle multiple AND operators
    while (match(AND)) { // Check if the next token is an AND operator
        Token *oper = new Token(previous()); // Get the token for the AND operator
        Expr *right = equality(); // Parse the right-hand side expression
        // Create a Logical expression node representing the AND operation
        expr = new Logical(expr, oper, right);
    }

    return expr; // Return the parsed expression
}

– Parse Equality Expression:

• The method starts by calling the equality() method to parse an equality expression.
• The equality() method likely handles parsing equality operations (==, !=) and expressions with higher precedence.

– Handle Multiple AND Operators:

• While there are consecutive AND operators (&&) in the source code, the method continues to parse equality expressions on the right-hand side of each AND operator.
• For each AND operator encountered, it creates a Logical expression node representing the AND operation between the previously parsed expression (expr) and the newly parsed right-hand side expression.

Expr * Parser::equality() {
    Expr *expr = comparison(); // Parse a comparison expression

    // Loop to handle multiple equality or inequality operators
    while (match(EQUAL_EQUAL) || match(BANG_EQUAL)) { // Check if the next token is either == or !=
        Token *oper = new Token(previous()); // Get the token for the equality or inequality operator
        Expr *right = comparison(); // Parse the right-hand side expression
        // Create a Binary expression node representing the equality or inequality comparison
        expr = new Binary(expr, oper, right);
    }

    return expr; // Return the parsed expression
}

– Parse Comparison Expression:

• The method starts by calling the comparison() method to parse a comparison expression.
• The comparison() method likely handles parsing comparison operations (<, <=, >, >=) and expressions with higher precedence.

– Handle Multiple Equality or Inequality Operators:

• While there are consecutive equality (==) or inequality (!=) operators in the source code, the method continues to parse comparison expressions on the right-hand side of each operator.
• For each equality or inequality operator encountered, it creates a Binary expression node representing the comparison operation between the previously parsed expression (expr) and the newly parsed right-hand side expression.

Expr * Parser::comparison() {
    Expr *expr = term(); // Parse a term expression

    // Loop to handle multiple comparison operators
    while (match(LESS) || match(GREATER) || match(LESS_EQUAL) || match(GREATER_EQUAL)) {
        Token *oper = new Token(previous()); // Get the token for the comparison operator
        Expr *right = term(); // Parse the right-hand side expression
        // Create a Binary expression node representing the comparison operation
        expr = new Binary(expr, oper, right);
    }

    return expr; // Return the parsed expression
}

– Parse Term Expression:

• The method starts by calling the term() method to parse a term expression.
• The term() method likely handles parsing basic arithmetic expressions involving multiplication, division, and unary operators.

– Handle Multiple Comparison Operators:

• While there are consecutive comparison operators (<, >, <=, >=) in the source code, the method continues to parse term expressions on the right-hand side of each operator.
• For each comparison operator encountered, it creates a Binary expression node representing the comparison operation between the previously parsed expression (expr) and the newly parsed right-hand side expression.

Expr * Parser::term() {
    Expr *expr = factor(); // Parse a factor expression

    // Loop to handle multiple addition or subtraction operators
    while (match(MINUS) || match(PLUS)) {
        Token *oper = new Token(previous()); // Get the token for the addition or subtraction operator
        Expr *right = factor(); // Parse the right-hand side expression
        // Create a Binary expression node representing the addition or subtraction operation
        expr = new Binary(expr, oper, right);
    }

    return expr; // Return the parsed expression
}

– Parse Factor Expression:

• The method starts by calling the factor() method to parse a factor expression.
• The factor() method likely handles parsing basic arithmetic expressions involving multiplication, division, and unary operators.

– Handle Multiple Addition or Subtraction Operators:

• While there are consecutive addition (+) or subtraction (-) operators in the source code, the method continues to parse factor expressions on the right-hand side of each operator.
• For each addition or subtraction operator encountered, it creates a Binary expression node representing the addition or subtraction operation between the previously parsed expression (expr) and the newly parsed right-hand side expression.

Expr * Parser::factor() {
    Expr *expr = unary(); // Parse a unary expression

    // Loop to handle multiple multiplication or division operators
    while (match(STAR) || match(SLASH)) {
        Token *oper = new Token(previous()); // Get the token for the multiplication or division operator
        Expr *right = unary(); // Parse the right-hand side expression
        // Create a Binary expression node representing the multiplication or division operation
        expr = new Binary(expr, oper, right);
    }

    return expr; // Return the parsed expression
}

– Parse Unary Expression:

• The method starts by calling the unary() method to parse a unary expression.
• The unary() method likely handles parsing unary operators (such as negation or logical negation) and primary expressions.

– Handle Multiple Multiplication or Division Operators:

• While there are consecutive multiplication (*) or division (/) operators in the source code, the method continues to parse unary expressions on the right-hand side of each operator.
• For each multiplication or division operator encountered, it creates a Binary expression node representing the multiplication or division operation between the previously parsed expression (expr) and the newly parsed right-hand side expression.

Expr * Parser::unary() {
    // Check if the current token is a unary operator
    if (match(MINUS) || match(BANG) || match(STAR) || match(SLASH) || match(PLUS)) {
        // Check if the previous token was also a unary operator
        if ((previous().type == MINUS) || (previous().type == BANG)) {
            Token *oper = new Token(previous()); // Get the token for the unary operator
            Expr *right = unary(); // Parse the right-hand side expression recursively
            return new Unary(oper, right); // Create a Unary expression node representing the unary operation
        } else {
            error(previous(), "Missing left operand."); // Report an error if there's a unary operator without a left operand
            return nullptr;
        }
    }
    return call(); // If there's no unary operator, parse the call expression
}

– Check for Unary Operator:

• The method checks if the current token is a unary operator (-, !, *, /, +).

– Parse Unary Expression:

• If the previous token was also a unary operator (- or !), it recursively calls unary() to parse the right-hand side expression.
• It creates a Unary expression node representing the unary operation with the operator token and the parsed right-hand side expression.

– Handle Missing Left Operand:

• If there's a unary operator without a left operand, it reports an error indicating a missing left operand.
• It returns nullptr to signify that parsing of the unary expression failed due to the error.

– Parse Call Expression:

• If there's no unary operator, it delegates the parsing to the call() method, which likely handles parsing function calls or primary expressions.

Expr * Parser::call() {
    Expr *expr = primary(); // Parse a primary expression

    // Loop to handle function calls and property access
    while (true) {
        if (match(LEFT_PAREN)) { // Check if the next token is a left parenthesis (indicating a function call)
            expr = finishCall(expr); // Parse the function call and update the expression
        } else if (match(DOT)) { // Check if the next token is a dot (indicating property access)
            if (consume(IDENTIFIER, "Expect property name after '.'.")) { // Check if there is an identifier token after the dot
                // Create a Get expression node representing the property access
                expr = new Get(expr, new Token(previous()));
            } else {
                break; // Break the loop if there is no identifier after the dot
            }
        } else {
            break; // Break the loop if neither function call nor property access is detected
        }
    }

    return expr; // Return the parsed expression
}

– Parse Primary Expression:

• The method starts by calling the primary() method to parse a primary expression.
• The primary() method likely handles parsing basic expressions such as literals, identifiers, or parenthesized expressions.

–  Loop for Function Calls and Property Access:

• The method enters an infinite loop to handle function calls and property access.
• Inside the loop:
  • If the next token is a left parenthesis ((), it indicates a function call, so the finishCall() method is called to parse the arguments and update the expression.
  • If the next token is a dot (.), it indicates property access. If there is an identifier token after the dot, a Get expression node is created to represent the property access.
  • If neither a left parenthesis nor a dot is detected, the loop breaks.

Expr * Parser::primary() {
    // Check various possible types of primary expressions
    if (match(TRUE_TOKEN)) {
        return new Literal(new Object(true)); // Return a Literal expression representing true
    } else if (match(FALSE_TOKEN)) {
        return new Literal(new Object(false)); // Return a Literal expression representing false
    } else if (match(NIL)) {
        return new Literal(new Object()); // Return a Literal expression representing null
    } else if (match(NUMBER)) {
        Token t = previous(); // Get the token representing the number
        return new Literal(new Object(t.literal)); // Return a Literal expression representing the number
    } else if (match(STRING)) {
        Token t = previous(); // Get the token representing the string
        return new Literal(new Object(t.literal)); // Return a Literal expression representing the string
    } else if (match(LEFT_PAREN)) {
        Expr *expr = expression(); // Parse an expression within parentheses
        if (consume(RIGHT_PAREN, "Expected ')' after expression.")) {
            return new Grouping(expr); // Return a Grouping expression representing the parenthesized expression
        } else {
            // Error occurred, allow to recover by returning the expression
            return expr;
        }
    } else if (match(THIS)) {
        return new This(new Token(previous())); // Return a This expression representing 'this'
    } else if (match(IDENTIFIER)) {
        return new Variable(new Token(previous())); // Return a Variable expression representing an identifier
    } else if (match(SUPER)) {
        Token *keyword = new Token(previous()); // Get the token representing 'super'
        consume(DOT, "Expect '.' after 'super'."); // Consume the dot after 'super'
        if (consume(IDENTIFIER, "Expect superclass method name.")) {
            Token *method = new Token(previous()); // Get the token representing the superclass method name
            return new Super(keyword, method); // Return a Super expression representing a superclass method call
        }
        return nullptr;
    } else if (match(FUN)) {
        return (Expr *)function("lambda"); // Parse and return a lambda function expression
    } else if (isAtEnd()) {
        return nullptr; // Return null if there are no more tokens
    }
    error(peek(), "Expected expression."); // Report an error if none of the expected primary expressions are matched
    return nullptr; // Return null to signify failure to parse a primary expression
}

– Check Various Primary Expression Types:

• The method checks various possible types of primary expressions using match() for keywords like true, false, nil, numbers, strings, left parenthesis, this, identifiers, super, and fun.

– Parse Primary Expressions:

• Depending on the matched token, the method parses and constructs corresponding expression nodes:
  • For boolean literals (true and false), nil, numbers, and strings, it constructs Literal expressions.
  • For expressions within parentheses, it parses the contained expression recursively and constructs a Grouping expression.
  • For this, super, and identifiers, it constructs This, Super, and Variable expressions, respectively.
  • For lambda functions, it calls the function() method to parse and construct lambda function expressions.

– Handle Errors and End of Input:

• If there are no more tokens (isAtEnd()), it returns nullptr.
• If none of the expected primary expressions are matched, it reports an error.

Since our lexeme after PRINT is “Hi” (string). So, below if block is executed.

	else if (match(STRING)) // match will check if the current token type is "string" and advances the current pointer.
    {
        Token t = previous(); // store the string because current was advanced in match statement.
        return new Literal(new Object(t.literal));
    }

• This function checks if the current token is a string literal.
• If the current token is indeed a string literal, the previous() function retrieves the token immediately before the current one, which is the string literal token.
• new Literal(new Object(t.literal)): It constructs a Literal expression node with the string literal value obtained from the token. The Object class encapsulated different type of literals, and here, it's used to create an object holding the string literal value.
• The constructed Literal expression node representing the string literal is returned.

struct Literal : public Expr
{
    Object *value;

    Literal(Object *value) : Expr(ExprType_Literal), value(value) {}

    ~Literal();
};

enum ExprType
{
    ExprType_Assign,
    ExprType_Ternary,
    ExprType_Binary,
    ExprType_Logical,
    ExprType_Grouping,
    ExprType_Literal,
    ExprType_Set,
    ExprType_Super,
    ExprType_This,
    ExprType_Unary,
    ExprType_Variable,
    ExprType_Call,
    ExprType_Get,
    ExprType_Lambda,
};

struct Expr
{
    ExprType type;
    Expr(ExprType type) : type(type) {}
    virtual ~Expr() {}
};

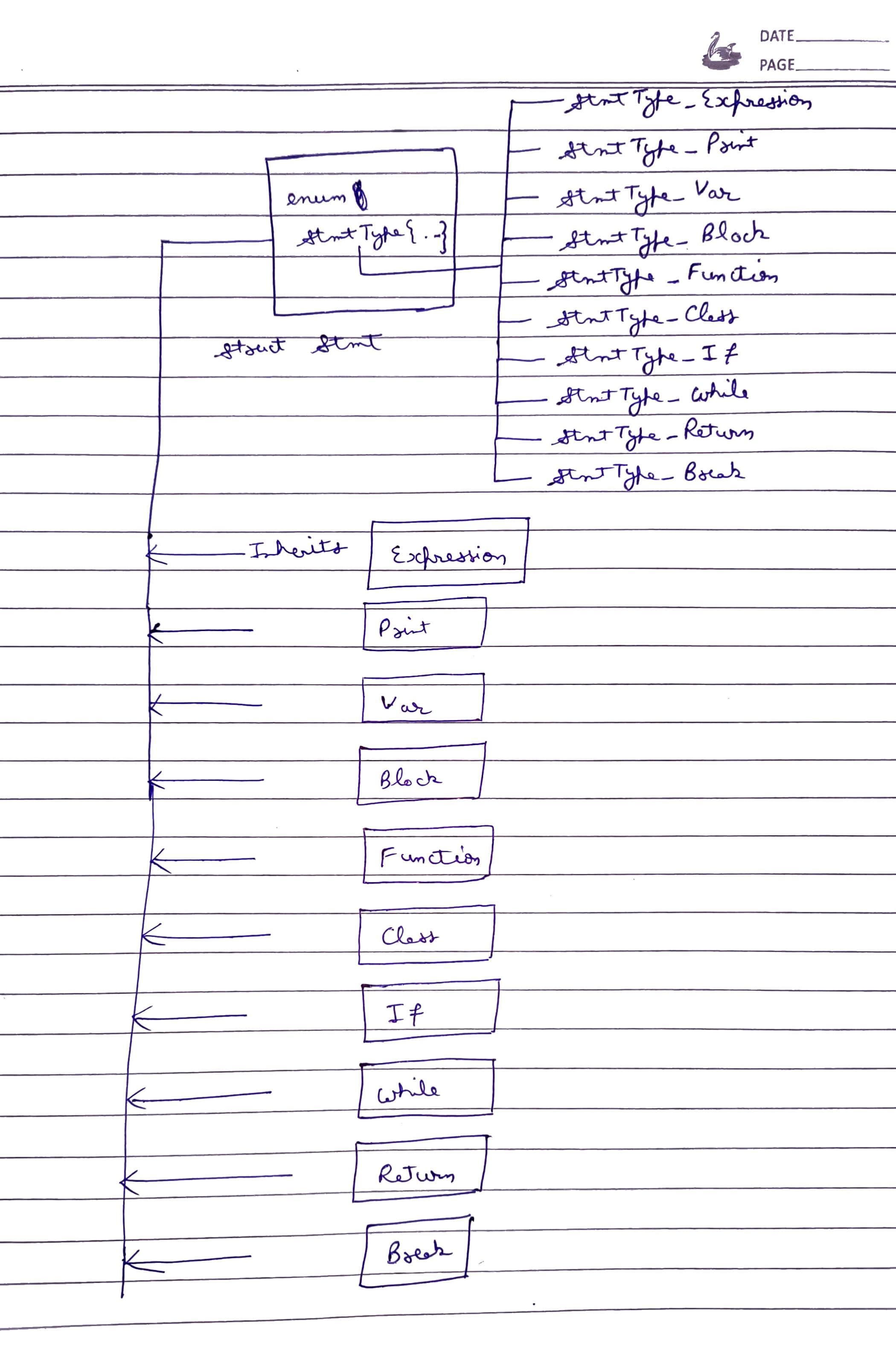
#4 Output From Parser

    std::vector<Stmt *> statements = parser.parse();

The parser is responsible for analyzing the structure of the input code, verifying its correctness, and building a structured representation of the code known as an abstract syntax tree(AST).

It returns a vector of statement objects (Stmt).