Water Bottles

Problem Statement

There are numBottles water bottles that are initially full of water. You can exchange numExchange empty water bottles from the market with one full water bottle.

The operation of drinking a full water bottle turns it into an empty bottle.

Given the two integers numBottles and numExchange, return the maximum number of water bottles you can drink.

Constraints:

• 1 ≤ numBottles ≤ 100
• 2 ≤ numExchange ≤ 100

LeetCode:

Water Bottles

Examples

Example 1:

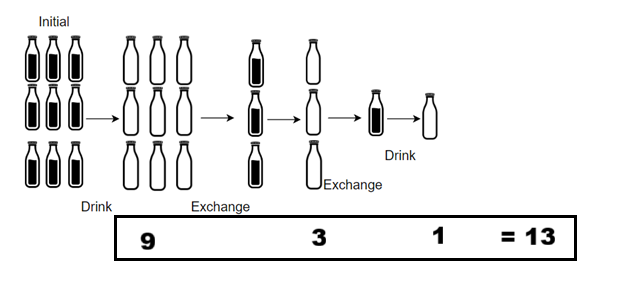
Input: numBottles = 9, numExchange = 3
Output: 13

Explanation: You can exchange 3 empty bottles to get 1 full water bottle.
Number of water bottles you can drink: 9 + 3 + 1 = 13

Example 2:

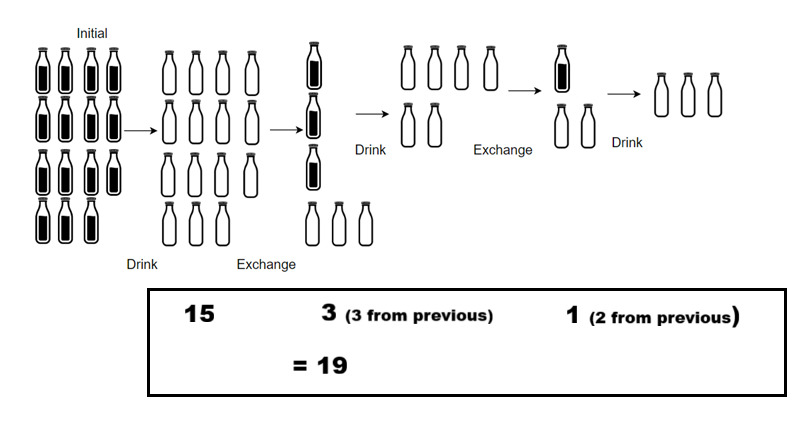
Input: numBottles = 15, numExchane = 4
Output: 19

Explanation: You can exchange 4 empty bottles to get 1 full water bottle.
Number of water bottles you can drink: 15 + 3 + 1 = 19

Different Approaches

1️⃣ Simulation

Intuition:

Think about this problem like a real-life recycling program:

• You drink your initial bottles -> they all become empty.
• Whenever you collect enough empties, you go back to the shop and exchange them for new full bottles.
• You drink those too, adding more empties.
• Repeat until you no longer have enough empties for an exchange.

This is a loop of drinking and exchanging.

Approach:

We directly simulate the process:

1. Initialize:
   1. total = numBottles (since you will drink them anyway).
   2. empty = numBottles (after drinking).
2. While you have enough empties (empty >= numExchange):
   1. Exchange: newBottles = empty / numExchange.
   2. Drink them: total += newBottles.
   3. Update empties:

      1. empty = (empty % numExchange) + newbottles

         (leftover empties + new empties from drinking).

3. Return total.

Code in C++:

class Solution {
public:
    int numWaterBottles(int numBottles, int numExchange) {
        int totalDrank = numBottles;
        int empty = numBottles;

        while (empty >= numExchange) {
            int newBottles = empty / numExchange;   // bottles you get
            totalDrank += newBottles;              // drink them
            empty = empty % numExchange + newBottles; // leftover + new empties
        }

        return totalDrank;
    }
};

Complexity Analysis:

• Time Complexity:
  • Each exchange reduce the number of empties.
  • Worst case, it runs proportional to the number of bottles you can drink. 
  • O(numBottles / numExchange) -> very small
• Space Complexity:O(1)
  • No extra variables used.