In order to understand the Heap data structure, firstly we have to know about the complete binary tree.

Almost Complete Binary Tree

A complete binary tree is a binary tree in which every level, except possibly the last, is completely filled, and all nodes are as far left as possible.

Key Properties of a Almost Complete Binary Tree:

1. Level Order: All levels of the tree are fully filled, except possibly the last level.
2. Left-Justified: All nodes at the last level are placed as far left as possible.

Visual Representation of Complete Binary Trees:

Example 1: Complete Binary Tree of Depth 0 (Only the Root Node)

    1

• Depth: 0 (Only one node, the root).
• Total nodes: 1.

Example 2: Complete Binary Tree of Depth 1

      1
     / \
    2   3

• Depth: 1 (The root has two children).
• Total nodes: 3

Example 3: Complete Binary Tree of Depth 2

          1
        /   \
       2     3
     /   \   /   \
    4     5 6     7

• Depth: 2 (Each non-leaf node has two children)
• Total nodes: 7

Example 4: Complete Binary Tree of Depth 3

            1
        /       \
       2         3
     /   \      /   \
    4     5    6     7
   / \   / 
  8   9 10

• Depth: 3 (The last level is not fully filled, but all nodes are as far left as possible)
• Total nodes: 10

Heap

A heap is a specialized tree-based data structure that satisfies the heap property. It is commonly used to efficiently solve problems involving priority and to implement algorithms like sorting and finding the smallest or largest elements.

Heap Property:

The heap property defines the relationship between a parent node and its child nodes in a heap. This property ensures that the structure of the heap remains consistent for efficient operations. The exact nature of this relationship depends on the type of heap. There are two types of heaps:

1. Min-Heap: The value of each parent node must be less than or equal to the values of its child noes. This ensures that the smallest element is always at the root of the heap.
2. Max-Heap: The value of each parent node must be greater than or equal to the values of its child nodes. This ensures that the largest element is always at the root of the heap.

Key Points about the Heap Property:

1. Local Relationship:

   The heap property only ensures that a parent node maintains its relationship with its immediate children. It does not impose any order between sibling nodes or across levels.

2. Preservation During Operations:

   When elements are inserted or removed, the heap property might temporarily be violated. A process heapification restores the property by adjusting the positions of elements.

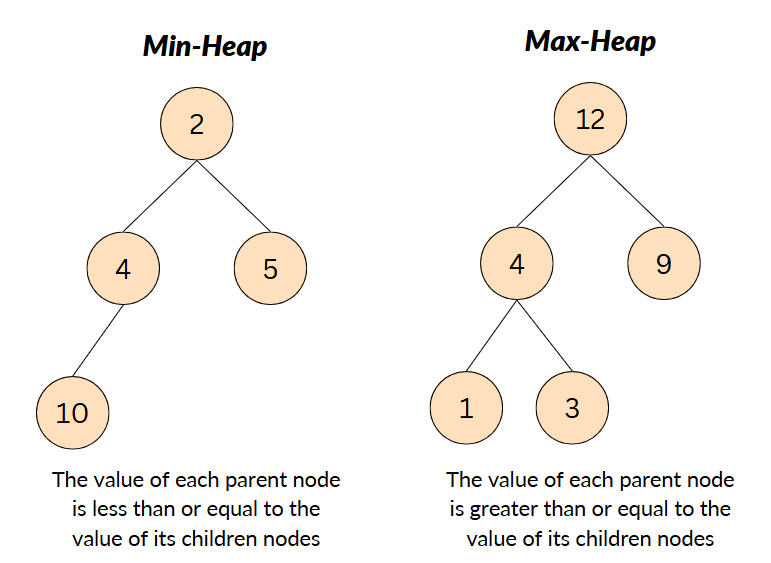
Representation of Heap

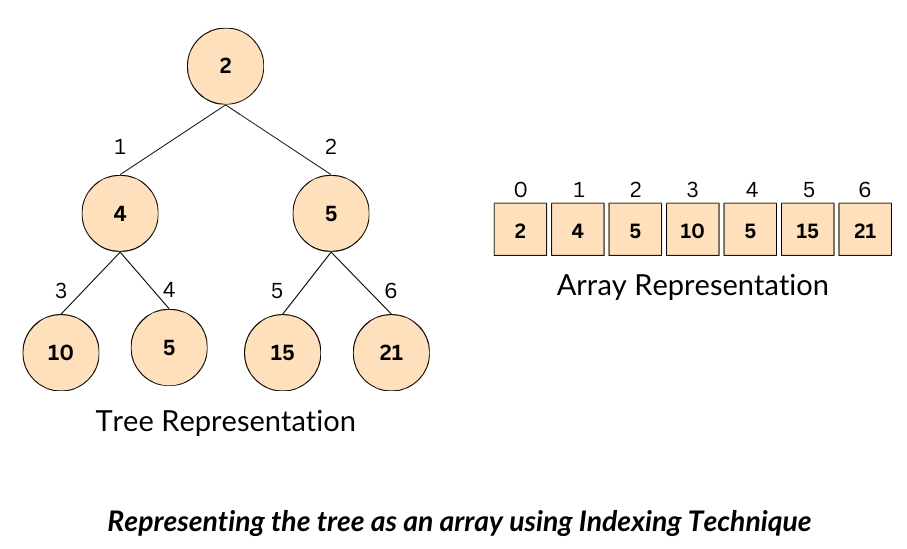
The internal implementation of a heap utilizes the array representation of a heap rather than the tree structure discussed earlier. This highlights the importance of understanding how an almost complete binary tree is represented using an array.

Indexing Technique to Represent the Tree;

• Root Node: The root of the tree is stored at index 0 (following the 0-based indexing).
• Parent-Child Relationships: For a node at index i:
  • Left Child: The left child is located at index 2*i + 1
  • Right Child: The right child is located at index 2*i + 2.
  • Parent is located at index [i / 2] - 1.
    • OR [i - 1] / 2.

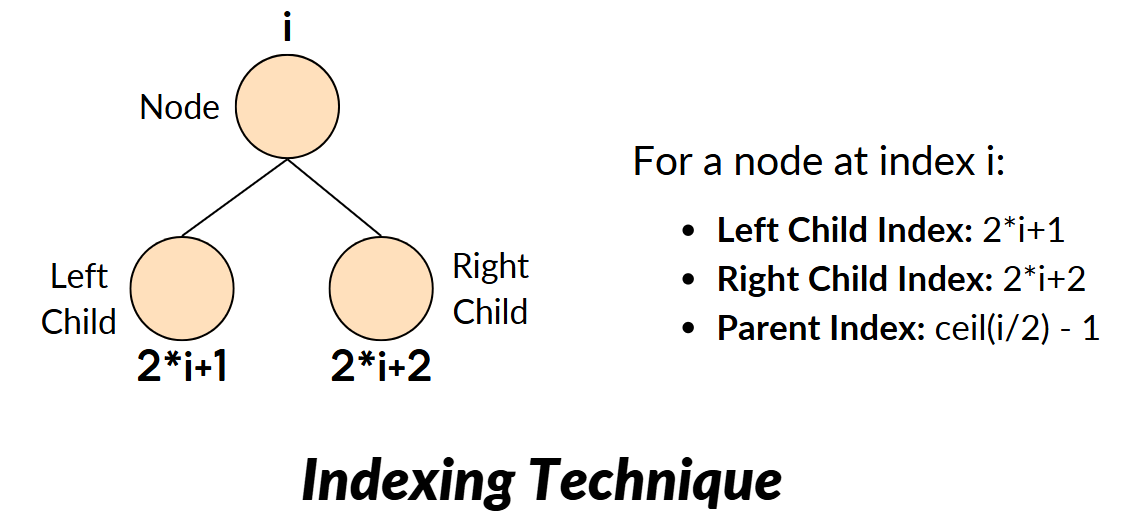
Example Conversion:

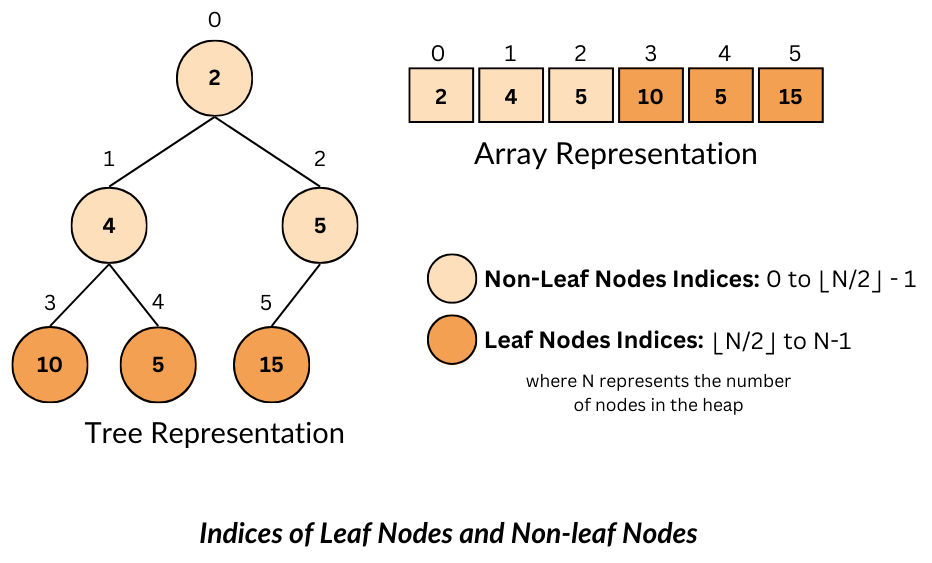
Indices of Leaf Nodes and Non-leaf Nodes

Leaf Nodes:

• Leaf nodes are the nodes without any children, and they always appear in the last level (or partially in the second last level if the last level is incomplete).
• In the array representation of a binary tree with N elements:
  • Range of Leaf Node Indices: Leaf Nodes start from the index [N/2] to [N - 1] (both inclusive).

Non-leaf Nodes:

• Non-leaf nodes are the nodes that have at least one child.
• In the array representation of a binary tree with N elements.
  • Range of Non-leaf Indices: Non-leaf Nodes start from the index 0 to [N/2] - 1 (both inclusive).

Example:

Why Heap are represented as the Almost Complete Binary Tree?

The almost complete binary tree allows the heap to be stored compactly in an array, eliminating the need for additional pointers or complex node structures.

• The root is at index 0.
• For any node at index i:
  • The left child is at 2i + 1.
  • The right child is at 2i + 2.
  • The parent is at (i - 1) / 2.

If the tree is not almost complete, gaps (unoccupied positions) would appear in the array. This would result in:

1. Wasted Space: Empty indices in the array would consume unnecessary memory.
2. Broken Index Relationships: Parent-child relationships, which are based on indices would no longer be straightforward. This would make accessing children or parents computationally expensive.

Example:

Consider this non-complete binary tree:

        10
       /  
     15    
      \     
      30  

Its array representation would look like:

[10, 15, _, 30, _, _, ...]

• The gap (_) at index 2 breaks the left-right child relationships, making traversal or heapify operations inefficient and error-prone.
• Wastes space and complicates navigation.

Consider almost complete binary tree:

        10
       /  \
     15    30
    / \   /
   40 50 100

Array representation:

[10, 15, 30, 40, 50, 100]

It forms a sequence that it is stored in level wise from left to right, which makes it efficient, compact and easy to navigate.